The primary distinction between angular acceleration vs centripetal acceleration is that angular acceleration is the rate of change of angular velocity with respect to time, whereas centripetal acceleration is the acceleration found in an object rotating in a circular path caused due to the constant change in the direction of the motion.
Contents:
Angular acceleration:
Angular acceleration is the rate of change of angular speed with respect to time. It is denoted by the symbol ‘α’ and measured in terms of rad/s².
The term angular acceleration is analogous to linear acceleration in linear motion.
It is given by,
α = `\mathbf{\frac{d\omega}{dt}}`
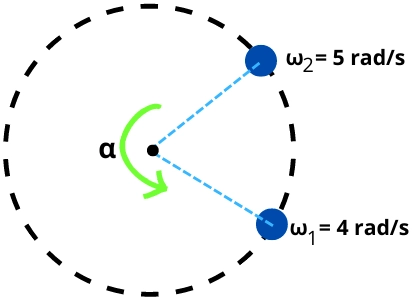
The above figure indicates the angular velocities of the object at two different positions within a time interval (`t_{12}`) of 5 seconds.
Thus the angular acceleration of the object while moving from position 1 to 2 is given by,
α = `\frac{\omega_{2}-\omega_{1}}{t_{12}}`
α = `\frac{5-4}{5}`
α = 0.2 rad/s²
Centripetal acceleration:
Centripetal acceleration (Radial acceleration) causes due the constantly changing direction of the object undergoing circular motion and it is always directed towards the center of rotation.
It is denoted by the symbol `a_{c}` and measured in terms of the m/s².
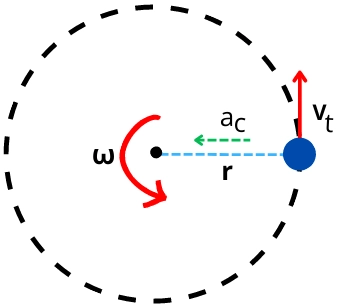
The above figure shows the object moving in the circular path with a tangential velocity of `v_{t}`.
In this case, the centripetal acceleration acting on the object is given by,
`a_{c}` = `\frac{v_{t}^{2}}{r}`
The above equation indicates that the centripetal acceleration in the object is directly proportional to the square of the tangential velocity and inversely proportional to the radius of rotation of the object.
Angular acceleration vs Centripetal acceleration:
| Sr. No. | Angular acceleration | Centripetal acceleration |
|---|---|---|
| 1 | It is a rate of change of angular velocity with respect to time. | It is the acceleration in the object undergoing circular motion because of the continuous change in direction of motion. |
| 2 | Angular acceleration occurs due to a change in the angular velocity of the object. | Centripetal acceleration occurs due to the continuous change in the direction of the tangential velocity of the object. |
| 3 | The direction of angular acceleration never depends on the position of the object. | The direction of centripetal acceleration constantly changes based on the position of the revolving object. |
| 4 | Zero angular acceleration indicates that the object is revolving with constant angular velocity or the object is not revolving. | Zero centripetal acceleration indicates that the object is not moving in a circular path. |
| 5 | The object can rotate even with zero angular acceleration. | The centripetal acceleration of the revolving object never becomes zero. |
| 6 | It is denoted by the symbol ‘α’ and measured in terms of rad/s². | It is denoted by the symbol ‘`a_{c}`’ or ‘`a_{r}`’ and measured as m/s². |
| 7 | Angular acceleration is given by, α = `\frac{d\omega}{dt}` | Centripetal acceleration is given by, `a_{c}` = `\frac{v_{t}^{2}}{r}` = `r\omega^{2}` |
| 8 | Angular acceleration is the term used in an angular motion. | It is a term used in linear motion. |
FAQ:
Does angular acceleration affect centripetal acceleration?
No, the angular acceleration never affects the centripetal acceleration.
Related comparisons: