Kinetic energy is the energy associated with the object due to its motion, but does it also become negative?
Kinetic energy is never negative in classical physics; it may be negative in quantum mechanics. In classical physics, the kinetic energy depends on mass and square of speed, which are always positive. In quantum mechanics, when the particle’s potential energy is higher than the total energy, KE is considered as negative.
Contents:
Continue reading to learn why Kinetic energy is considered positive or negative in different studies.
Why Kinetic energy can’t be negative in Classical physics?
In classical physics, Kinetic energy can’t be negative; it may be positive or zero. The object possesses kinetic energy due to its mass (m) and speed (V2).
`K.E. = \frac{1}{2}m.V^{2}`
Here are some of the reasons why kinetic energy is always positive:
1] Mass never be negative: The mass indicates the amount of matter that exists in an object. Thus, it always possesses a positive sign. A negative mass is not possible.
2] Square of speed is always positive: The object may move in a positive or negative direction (+V or -V), but due to the squaring, the V2 term always becomes positive.
The product of these two positive terms becomes positive; therefore, the kinetic energy always remains positive.
Let’s understand it with the below example.
The below figure shows the position of the ball (mass 0.5 Kg) thrown vertically.
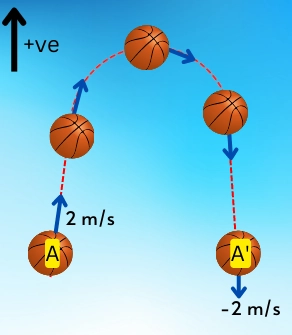
As per the consideration provided in the image, while moving up, the ball possesses positive velocity while moving down, it possesses negative velocity.
For the ball at A (moving upward), the kinetic energy is given by,
`KE_{A} = \frac{1}{2}mV_{A}^{2} = \frac{1}{2}\times0.5\times(2)^{2} = 1 J`
For the ball at A’ (moving downward), the kinetic energy is given by,
`KE_{A’} = \frac{1}{2}mV_{A’}^{2} = \frac{1}{2}\times0.5\times(-2)^{2} = 1 J`
Thus from the above results, it becomes clear that the KE in classical physics always stays positive.
Can kinetic energy be negative in Quantum mechanics?
In quantum mechanics, kinetic energy is considered as positive as well as negative.
The particle possesses a negative kinetic energy when the total energy ‘E’ is less than the potential energy ‘V0‘.
K.E. = E – V0
∴ K.E. becomes negative when, E<V0.
The region where the particles have negative kinetic energy (E<Vx) is known as a Classically forbidden region.
Quantum tunneling is the phenomenon that has a probability of the particles possessing Negative kinetic energy.
Can change in Kinetic energy be negative in Classical physics?
A change in kinetic energy indicates the difference between the kinetic energy at the initial state and the final state.
`\Delta K.E. = KE_{\text{final}} -KE_{\text{initial}}`
`\Delta K.E. = \frac{1}{2}m.V_{\text{final}}^{2} – \frac{1}{2}m.V_{\text{initial}}^{2}`
`\Delta K.E. = \frac{1}{2}m.[V_{\text{final}}^{2} – V_{\text{initial}}^{2}]`
When an object slows down, its initial speed is higher than the final speed (Vinitial > Vfinal). In such cases, as per the above formula, the change in kinetic energy becomes negative.
Example: While stopping the car, the driver presses the brake pedal. It lowers the speed of the car.
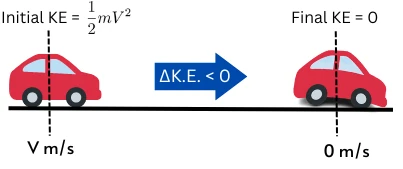
Here the change in kinetic energy is given by,
`\Delta K.E. = \frac{1}{2}m.[0 – V^{2}]`
`\Delta K.E. = -\frac{1}{2}m.V^{2}`
In this example, the kinetic energy of the car decreases during braking and hence the change in kinetic energy becomes negative.
Read also: