Center of pressure (Physics) Definition, Formula, Derivation

We know that the fluid exerts hydrostatic pressure on the surface of the object due to the weight of the fluid particles. This pressure increases with the increase in depth from the free surface of the liquid.

Thus the force acting on the object due to the hydrostatic pressure also varies over the surface of the object. The position of the resultant of these hydrostatic forces is denoted by the center of pressure.

Thus in this article, we are discussing one of the vital topics in fluid mechanics, i.e. center of pressure.

What is a Center of pressure?

The Center of pressure is the point of application of total pressure force (Resultant hydrostatic force) exerted by the liquid on the object.

The position of the center of pressure is generally expressed as its perpendicular distance from the free surface of the liquid (h*).

The force ‘F’ in the below figure indicates the total pressure force developed by the fluid on the object, while the h* indicates the distance of the center of pressure (COP) from the free surface of the liquid.

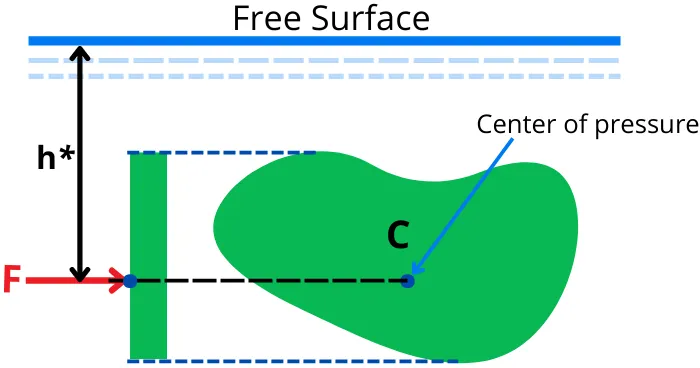
The center of pressure is found in such a way that the moment of the total pressure force, F (acting at the center of pressure) about the free surface is equivalent to the sum of the moment developed by each of the individual hydrostatic forces about the free surface.

Center of pressure equation:

1] Plane surface submerged horizontally in liquid:-

In this case, the COP is given by,

`h\text{*}=h`

Where ‘h’ is the depth of the plane surface from the free surface of the liquid.

2] Plane surface submerged vertically in liquid:-

For the plane surface submerged vertically in liquid, the COP is given by,

`h\text{*}=\frac{I_{G}}{A\bar{h}}+\bar{h}`

Where,
`I_{G}` = Moment of inertia about the centroidal axis of the object
A = Area of the plane surface
h̅ = Distance of CG from the free surface

3] Inclined plane surface submerged in liquid:-

For an inclined plane surface submerged in liquid, the COP is given by,

`h\text{*}=\frac{I_{G}sin^{2}\theta}{A\bar{h}}+\bar{h}`

Where,
θ = Angle between the plane and free surface

Center of pressure derivation:

1] For plane surface submerged horizontally in liquid:-

The below figure shows the plane surface submerged horizontally in liquid.

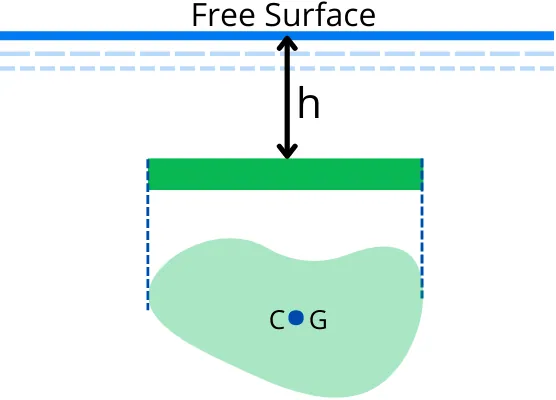
As the depth (h) is uniform for the whole surface, the hydrostatic pressure is also constant over the plane surface. Because of the uniform distribution of the pressure, the center of pressure acts at the center of gravity of the object.

Thus the depth of the center of pressure from the free surface of the liquid is given by,

`h\text{*} = h`

2] For plane surface submerged vertically in liquid:-

According to the varignon theorem, the sum of the moment of the coplanar forces about any point is equal to the moment of the resultant force about the same point.

Thus the location of the center of pressure can be found by comparing the moment of the resultant force about the free surface with the sum of the moment of the individual force about the free surface.

`\text{i.e.}\ M_{\text{Resultant force}} = \sumM_{\text{All forces}}\cdots[\text{Equation 1}]`

Let’s find each of them.

A] Sum of the moment of all hydrostatic forces (`\sumM_{\text{All forces}}`):

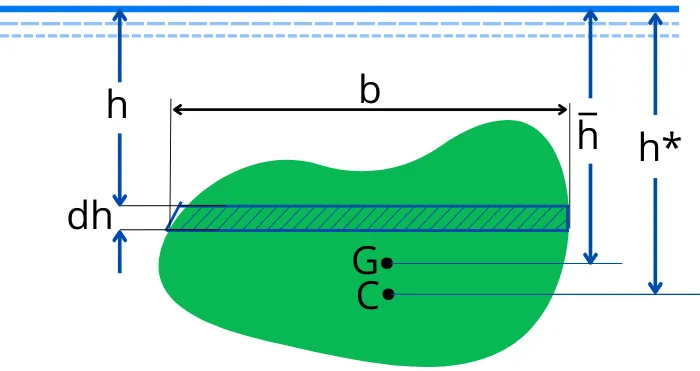
The above figure indicates the object submerged in the fluid with its center of gravity (G) at a distance of `\bar{h}` from the free surface.

Consider a small strip of width ‘b’ and height ‘dh’ located at a distance h from the free surface.

A small force ‘dF’ acting on the small strip is given by,

`dF= P \times dA`

[Where, `dA = dh \times b`]

As `P=\rhogh`,

`\thereforedF = \rho gh \times dA`

The moment of the small strip about the free surface is given by,

`M_{strip}=dF\times h`

`M_{strip} = [\rhogh(dA)]\times h`

`M_{strip} = \rhogh^{2}.dA`

The sum of the moment of all hydrostatic forces acting on the object about the free surface can be calculated by integrating the `M_{strip}`.

`\sumM_{\text{All forces}} = \intM_{strip} = \int\rhogh^{2}.dA`

`\sumM_{\text{All forces}} = \rhog\inth^{2}.dA`

As `\inth^{2}.dA=I` = Moment of inertia of an object about free surface

`\therefore \sumM_{\text{All forces}} = \rhogI`

By the parallel axis theorem, the moment of inertia of an object about the free surface is given by,

`I = I_{G}+A\bar{h}^{2}`

Where,
`I_{G}` = Moment of inertia about C.G.
A = Area of the plane surface
`\bar{h}` = Distance between the center of gravity and the free surface of the liquid

Put this value of `I` in the above equation of `\sumM_{\text{All forces}}`.

`\sumM_{\text{All forces}}= \rhog[I_{G}+A\bar{h}^{2}]`

B] Moment of a total hydrostatic force about the free surface (`M_{\text{Resultant}}`):

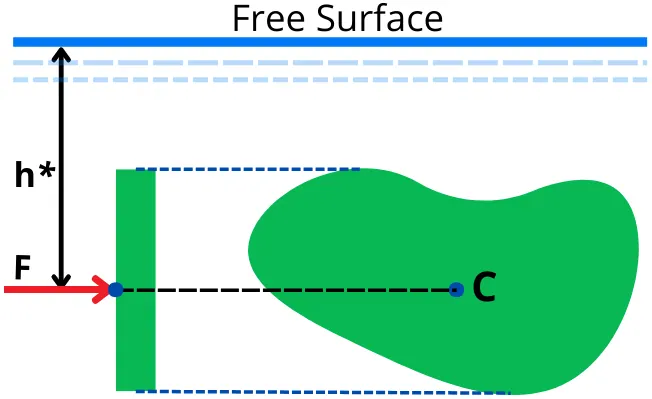
The total hydrostatic force (F) acts at the center of pressure (C), thus its moment about the free surface is given by,

`M_{\text{Resultant}} = F\timesh\text{*}`

As the total hydrostatic force, F = `\rhogA\bar{h}`

`\therefore M_{\text{Resultant}} = \rhogA\bar{h}\timesh\text{*}`

 Put these values of `\sumM_{\text{All forces}}` and `M_{\text{Resultant}}` in Equation-1.

`\therefore \rhog[I_{G}+A\bar{h}^{2}]=\rhogA\bar{h}\timesh\text{*}`

`h\text{*}=\frac{I_{G}}{A\bar{h}}+\bar{h}`

This is the equation to find the position of the center of pressure for the plane surface submerged vertically in liquid.

3] Inclined plane surface submerged in liquid:-

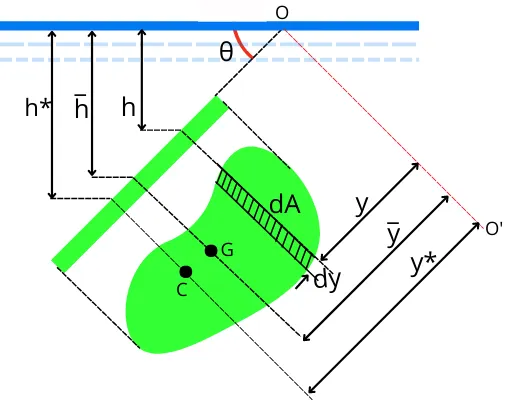
The above figure shows the plane surface submerged in a liquid inclined at an angle `\theta` from the free surface.

Where,
O-O’: Axis perpendicular to the inclined plane
`\bar{h}`: Distance between the center of gravity and the free surface of the liquid
h*: Distance of the center of pressure from the free surface
`\bar{y}`: Distance of the center of gravity from axis O-O’
y*: Distance of the center of pressure from axis O-O’

Consider a small strip of area ‘dA’ and thickness ‘dy’ located at a distance y from the axis O-O’.

From the above figure, we can say that,

`sin(\theta) = \frac{h}{y}=\frac{\bar{h}}{\bar{y}}=\frac{h\text{*}}{y\text{*}}`

∴ `h = ysin(\theta)\cdots[\text{Equation 2a}]`
`\bar{h}=\bar{y}sin(\theta)\cdots[\text{Equation 2b}]`
`h\text{*} = y\text{*}sin(\theta)\cdots[\text{Equation 2c}]`

The sum of the moment of all the forces about axis O-O’ is equal to the moment of the resultant hydrostatic force about the same axis,

`\thereforeM_{\text{Resultant}}=\sumM_{\text{All forces}}\cdots[\text{Equation 3}]`

Let’s find `M_{\text{Resultant}}` and `\sumM_{\text{All forces}}`.

A] Sum of the moment of all hydrostatic forces about axis O-O’ (`\sumM_{\text{All forces}}`):

The smaller force ‘dF’ acting on the strip is given by,

`dF = P\times\text{Area of the strip}`

As `P=\rhogh` and Area of the strip = dA, the equation becomes,

`dF = \rhogh.dA`

As, `h=ysin\theta`, therefore the equation becomes,

`dF = \rhog ysin\theta.dA`

Now the moment of small force ‘dF’ about axis ‘O-O’ is given by,

`M_{strip} = dF\timesy`

`M_{strip} = \rhog ysin\theta.dA \timesy`

`M_{strip} = \rhog y^{2}sin\theta.dA`

The sum of the moment of all hydrostatic forces about axis O-O’ is given by,

`\sumM_{\text{All forces}} = \intM_{strip} = \int\rhog y^{2}sin\theta.dA`

`\sumM_{\text{All forces}} = \rhog sin\theta\int y^{2}.dA`

As `\int y^{2}.dA=I` = Moment of inertia of the plane surface about axis O-O’

`\therefore \sumM_{\text{All forces}} = \rhog sin\theta.I\cdots[\text{Equation 4}]`

By parallel axis theorem, the moment of inertia about the axis O-O’ is also given by,

`I = I_{G}+A\bar{y}^{2}`

Where,
`I_{G}` = Moment of inertia about the centroidal axis
A = Area of the surface

From Equation-2b, `\bar{y} = \frac{\bar{h}}{sin\theta}`

∴ `I = I_{G}+A(\frac{\bar{h}}{sin\theta})^{2}`

`I = I_{G}+A(\frac{\bar{h}^{2}}{sin^{2}\theta})`

By putting this value of I in above equation 4, we get,

`\sumM_{\text{All forces}} = \rhog sin\theta.[ I_{G}+A(\frac{\bar{h}^{2}}{sin^{2}\theta})]`

B] Moment of a Resultant hydrostatic force about axis O-O’ (`M_{\text{Resultant}}`):

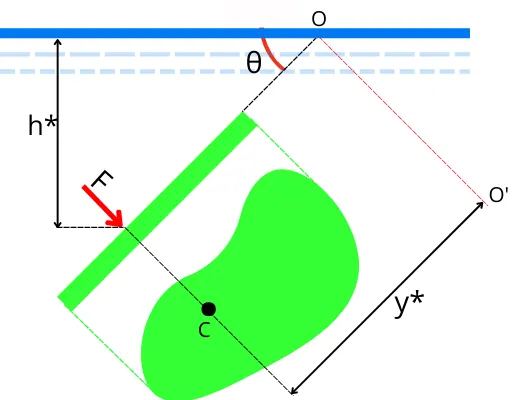
The resultant hydrostatic force on the inclined surface is given by,

`F = \rhogA\bar{h}`

The resultant hydrostatic force acts at the center of pressure, thus its moment about axis O-O’ is given by,

`M_{\text{Resultant}}=F\timesy\text{*}`

`M_{\text{Resultant}}=\rhogA\bar{h}\timesy\text{*}`

From above equation-2c, `y\text{*}=\frac{h\text{*}}{sin\theta}`

`\therefore M_{\text{Resultant}}=\rhogA\bar{h}\times(\frac{h\text{*}}{sin\theta})`

C] Center of pressure:

Now put the values of `M_{\text{Resultant}}` and `\sumM_{\text{All forces}}` in equation-3.

`\thereforeM_{\text{Resultant}}=\sumM_{\text{All forces}}`

`\rhogA\bar{h}\times(\frac{h\text{*}}{sin\theta}) =\rhog sin\theta.[ I_{G}+A(\frac{\bar{h}^{2}}{sin^{2}\theta})]`

`h\text{*}=\frac{sin^{2}\theta}{A\bar{h}}.[ I_{G}+A(\frac{\bar{h}^{2}}{sin^{2}\theta})]`

`h\text{*}=\frac{I_{G}.sin^{2}\theta}{A\bar{h}}+\bar{h}`

This is the equation to find the center of pressure of the plane surface submerged in liquid in an inclined position.

Solved examples:

The solved examples with calculations listed below will benefit you in understanding the topic center of pressure.

1] A square plate of side 150 mm is submerged vertically in water 1m below the free surface of the water. Find the position of the center of pressure from the free surface of the water. (Assume `\rho_{\text{water}}` = 1000 Kg/m³)

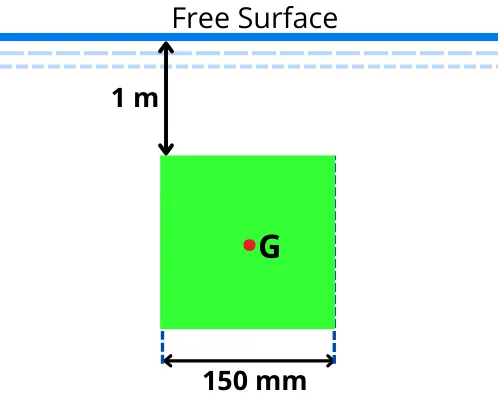
Given:
a = 150 mm = 0.15 m
`\rho` = 1000 Kg/m³

Solution:-

Step 1] Depth of center of gravity from the free surface (`\bar{h}`):

The position of center of gravity ‘G’ from the free surface is given by,

`\bar{h} = 1 + \frac{a}{2}`

`\bar{h} = 1 + \frac{0.15}{2}`

`\bar{h} = 1.075\ m`

Step 2] Area of the surface (A):

The area of the given plane surface is given by,

A = `a^{2}`

A = 0.15²

A = 0.0225 m²

Step 3] Moment of inertia about a centroidal axis (`I_{G}`):

The moment of inertia of the square surface about the centroidal axis is given by,

`I_{G} = \frac{a^{4}}{12}`

`I_{G} = \frac{0.15^{4}}{12}`

`I_{G} = 4.218\times10^{-5} m^{4}`

Step 4] COP (h*):

The position of the center of pressure for the vertically submerged plane surface is given by,

`h\text{*}=\frac{I_{G}}{A\bar{h}}+\bar{h}`

`h\text{*}=\frac{4.218\times10^{-5}}{0.0225\times1.075}+1.075`

h* = 1.0767 m

This is the distance of the center of pressure from the free surface of the fluid.

---

2] A circular plate submerged in water is inclined at `\theta` = 30° as shown in the figure. If the diameter of the circular plate is 300 mm, find the position of the center of pressure from the free surface.

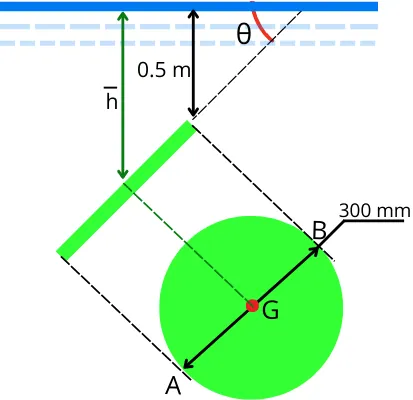
Given:
d = 300 mm = 0.3 m
`\theta` = 30°

Solution:-

Step 1] Depth of center of gravity from a free surface:

From the above figure, the distance `\bar{h}` is given by,

`\bar{h}=0.5+BGsin\theta`

`\bar{h}=0.5+BGsin(30)`

`\bar{h}=0.5+[\frac{0.3}{2}sin(30)]`

`\bar{h}=0.575\ m`

Step 2] Area of the plate:

The area of the given circular plane surface is given by,

`A=\frac{\pi}{4}.d^{2}`

`A=\frac{\pi}{4}.0.3^{2}`

A = 0.0706 m²

Step 3] Moment of inertia about the centroidal axis:

The moment of inertia of a circle about a centroidal axis is given by,

`I_{G}=\frac{\pi}{64}.d^{4}`

`I_{G}=\frac{\pi}{64}.0.3^{4}`

`I_{G}=3.976\times10^{-4}m^{4}`

Step 4] COP:

The position of the center of pressure of the plane surface submerged in fluid at an inclined position is given by,

`h\text{*}=\frac{I_{g}sin^{2}(\theta)}{A\bar{h}}+\bar{h}`

`h\text{*}=\frac{(3.976\times10^{-4})sin^{2}(30)}{0.0706\times0.575}+0.575`

h* = 0.577 m

This is the distance of the center of pressure of the inclined plate from the free surface.

FAQs:

Thanks for reading the blog post. We deeply explained about the center of pressure. Hope this blog post helped you. You can comment below for any queries regarding this topic.