Dual cycle: Definition, Process, Formula, PV & TS graph, Application

What is Dual cycle?

Dual cycle is the air standard cycle, which is a combination of the thermodynamic Otto cycle and Diesel cycle.

This thermodynamic power cycle consists of the two constant volume processes, two adiabatic processes, and one isobaric process (Constant pressure).

Dual cycle PV and TS diagram:

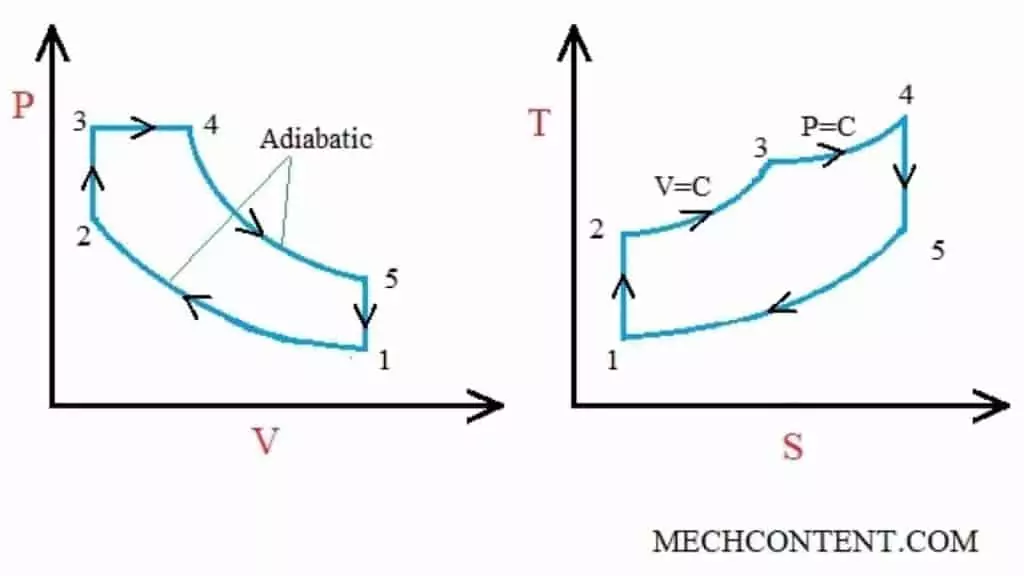
The cycle consists of following processes:

Process 1-2 (Isentropic compression): In this process, the air is compressed in isentropic (reversible adiabatic) manner from state 1 to 2.

Process 2-3 (Constant volume heat addition): During this process, the volume of the air is kept constant and heat is added externally to the air.

Process 3-4 (Constant pressure heat addition): In this process, the heat is added to the air by keeping the pressure constant.

Process 4-5 (Isentropic expansion): The high pressure air is expanded isentropically to obtain work.

Process 5-1 (Constant volume heat rejection): In this process, the heat is rejected by the air in adiabatic manner.

Thermodynamic analysis of cycle:

Let’s analyze each of the process in detail.

Process 1-2: Reversible adiabatic compression

For reversible adiabatic process,

Q_1-2 = 0

By compression of air from 1 to 2 temperature of air increases from T₁ to T₂ hence change in internal energy is given by :-

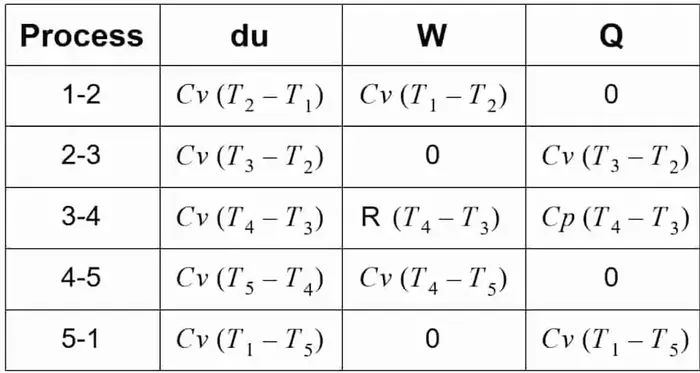
du_1-2 = C_v( T₂ – T₁)

Now by First law of thermodynamics,

Q_1-2 = du_1-2 +W_1-2

0 = C_v( T₂ – T₁) + W_1-2

W_1-2= C_v( T₁ – T₂ )

W_1-2 = C_v( T₁ – T₂ )

---

Process 2-3: Constant volume heat addition:

For the isochoric process, Change in volume (`delta v=0`)

∴ W_2-3 = 0

Here, temperature rises from T₂ to T₃. Hence, change in internal energy is given by,

du_2-3 = C_v( T₃-T₂ )

Now to find heat transfer (Q), By first law of thermodynamics,

Q_2-3 = du_2-3 + W_2-3

Q_2-3 = C_v( T₃ – T₂ ) + 0

Q_2-3 = C_v( T₃ – T₂ )

---

Process 3-4: Constant pressure heat addition:

For constant pressure process,

W_3-4 = P(V₄ – V₃)

As PV=RT, the above equation can write in the form of temperature as follows,

W_3-4 = R(T₄ – T₃)

The temperature rises from T₃ to T₄. Hence internal energy change is given by,

du_3-4 = C_v(T₄ – T₃)

Now to find rate of heat transfer by first law of thermodynamics,

Q_3-4 =du_3-4 + W_3-4

Q_3-4 = C_v( T₄ – T₃) + R(T₄ – T₃)

Q_3-4 = (C_v + R)(T₄ – T₃)

Q_3-4 = (C_v + C_p – C_v)(T₄ – T₃)

Q_3-4 = C_p( T₄ – T₃)

---

Process 4-5: Reversible expansion for the reversible adiabatic process:

Q_4-5 = 0

By expansion of air from 4 to 5, the temperature of the air decreases from T₄ to T₅. Hence, the change in internal energy is given by,

du_4-5 = C_v(T₅ -T₄)

Now, by the first law of thermodynamics,

Q_4-5 =du_4-5 + W_4-5

0 = C_v(T₅ – T₄) + W_4-5

W_4-5 = C_v(T₄ – T₅)

---

Process 5-1: Constant volume heat rejection:

For constant volume process,

W_5-1 = 0

In this process temperature of air decreases from T₅ to T₁. Hence, change in internal energy is given by,

du_5-1 = C_v(T₁ – T₅)

Now by first law of thermodynamics,

Q_5-1 =du_5-1 + W_5-1

Q_5-1 = C_v(T₁ – T₅) + 0

Q_5-1 = C_v( T₁ – T₅)

All parameters are summarized below:

Dual cycle application:

1] Heavy diesel engine.

Read also:

• Air standard Carnot cycle