Contents:
What is Endurance limit?
Endurance limit is the maximum value of the completely reversed stress for which the specimen can sustain for an infinite number of cycles without any fatigue failure.
Before discussing the endurance limit, it is necessary to know about fatigue failure.
Fatigue failure:- Failure in the material due to cyclic stress (complete reversed stress) is known as fatigue failure.
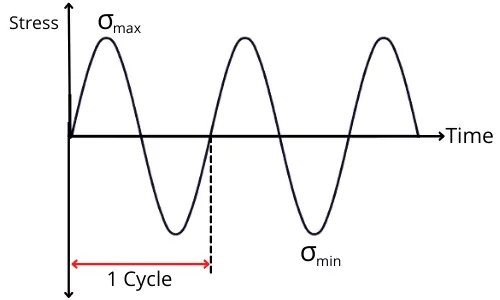
Consider a specimen with an ultimate tensile strength of `S_{ut}` subjected to the cyclic loading with the magnitude of cyclic stress is `\sigma_{t1}` < `S_{ut}`. For this stress, the object can withstand for `N_{1}` number of cycles before the fatigue failure.
Similarly, load the next same specimen having the same ultimate strength of `S_{ut}` for stress magnitude of `sigma_{t2}` where `sigma_{t2}` < `sigma_{t1}`. For this test, the object can withstand for `N_{2}` number of cycles before undergoing fatigue failure but now `N_{2}` > `N_{1}`.
In the same manner, if we perform the same experiment with decreasing magnitude of the completely reversed stress then the life of the specimen in case of a number of cycles also continuously increases.
But at a certain value of stress, the specimen can sustain up to an infinite number of cycles without any fatigue failure. This value of completely reversed stress is known as the endurance limit or endurance strength.
Endurance limit sn curve diagram:
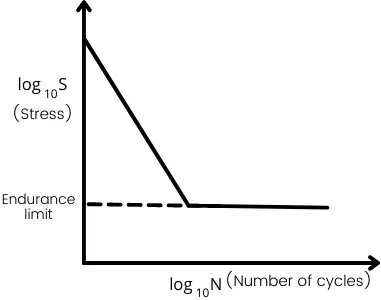
The above figure shows the plot of the cyclic stress and corresponding values of the number of cycles (N) performed before fatigue in the specimen.
As shown in the graph, for the higher value of the cyclic stress, the specimen withstands for less number of cycles but as the magnitude of cyclic stress decreases the number of cycles increases.
But at the endurance limit, the specimen can sustain up to an infinite number of cycles.
Endurance limit equation:
The actual endurance limit for the machine component is different from the endurance limit calculated for the standard specimen from the rotating beam experiment.
The actual value of endurance limit based on the various modifying factors is given by,
Se = Ka x Kb x Kc x Kd x Ke x Kg x`S_{e}^{‘}`
Here Ka, Kb, Kc, Kd, Ke and Kg are the modyfing factors.
Ka = Surface finish factor
Kb = Size factor
Kc = Load factor
Kd = Temperature factor
Ke = Stress concentration modifying factor
Kg = Reliability factor
Se’ = Endurance limit calculated for specimen
Endurance limit unit:
In the SI system, the unit endurance limit is Pascal (Pa). In the FPS system, the unit of the endurance limit is lb/ft².
How to determine endurance limit?
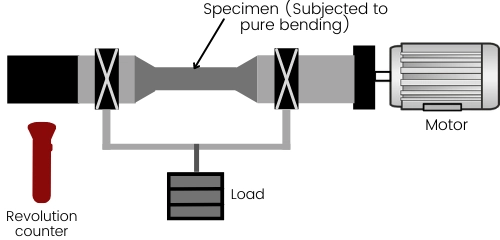
The endurance limit can be calculated by using a rotating-beam experiment. In this experiment, the standard specimen of the given material is mounted onto the experimental setup.
Because of the loads applied, the specimen is subjected to constant pure bending stress.
The motor attached to the specimen alters the direction of the bending stress by keeping the magnitude constant. Therefore the motor helps to create cyclic stress (completely reversed stress) into a specimen.
For finding the endurance limit, the specimen has to load with bending stress slightly less than ultimate tensile stress (`sigma_{1}` < `S_{ut}`). After that specimen is rotated with the help of a motor till the fracture occurs into the material. The number of cycles till the fracture is measured by the revolution counter.
In the next test, the next specimen is loaded with comparatively lower bending stress than the previous case (`sigma_{2}` < `sigma_{1}`). Perform the same experiment until the specimen fails and measure the cycles performed by the specimen.
Similarly, perform the same experiment by lowering the load in step by step manner and plot the results on the S-N curve.
As we decrease the load onto the specimen, the number of cycles performed by the specimen until fracture increases.
For the specimen at certain bending stress, the specimen will continuously rotate without causing any failure.
The corresponding stress applied in the specimen during this test is known as the endurance limit for this specimen (`S_{e}^{‘}`).
Endurance limit modifying factors:
The endurance limit is calculated for the standard specimen with standard size and highly finished surface based on the rotating beam experiment. But these results are not accurate for the machine components.
Therefore for the mechanical components, the actual endurance limit can be obtained by using different modifying factors. These modifying factors are listed below:-
a) Surface finish factors (Ka): The test specimen has a highly finished surface, but the surface finish of the machine component is poor as compared to the test specimen. The scratches present on the surface of the mechanical components can reduce the magnitude of the actual endurance limit. Therefore the surface finish factor helps to find the endurance limit of the actual machine component.
b) Size modification factor (Kb): As the size of the machine component increases, the endurance limit of the mechanical component decreases. Therefore the size modification factor helps to find the actual endurance limit based on the size of a machine component.
c) Load factor (Kc): The load modification factor finds the actual endurance limit based on different actual load conditions.
d) Temperature modification factor (Kd): The endurance limit of the machine component decreases with the increase in its operating temperature. Therefore the temperature modification factor helps to find the actual endurance limit based on the operating temperature.
e) Stress concentration modifying factor (Ke): The modifying factor for the stress concentration is inverse of the stress concentration factor (Kf) for fatigue failure.
f) Reliability factor (Kg): The reliability factor for the machine component affects the endurance limit of the machine component. The reliability modifying factor finds the actual endurance limit of the component based on the reliability.
Endurance limit example:
The endurance limit of the specimen is 100 N/mm², Find the actual endurance limit for the machine component if the modifying factors are, Ka = 0.7, Kb = 0.6, Kc = Kd = 1, Ke = 0.75, and Kg = 0.868.
Solution:-
Given:
Se’ = 100 N/mm²
Ka = 0.7
Kb = 0.6
Kc = Kd = 1
Ke = 0.75
Kg = 0.868
Se = ?
The actual endurance limit of the machine component is given by,
Se = Ka.Kb.Kc.Kd.Ke.Kg `S_{e}^{‘}`
Se = (0.7) x (0.6) x (1) x (1) x (0.75) x (0.868) x 100
Se = 27.342 N/mm²
Therefore the endurance limit for the machine component is 27.342 N/mm².
FAQ’s:
-
What is endurance limit of a metal?
For the metal component under cyclic loading, the endurance limit is the maximum value of the completely reversed stress at which the component can withstand up to an infinite number of cycles without any fatigue failure.
-
What is endurance limit formula?
The endurance limit for the machine component can be found by using this formula,
Se = Ka x Kb x Kc x Kd x Ke x Kg x Se’
Where Ka, Kb, Kc, Kd, Ke, and Kg are the modifying factors and Se’ is the endurance limit calculated for the standard specimen. -
What is endurance limit in SN curve?
For the S-N curve, the endurance limit is the maximum magnitude of stress at which the specimen can withstand infinite numbers of the stress cycles.
-
What is the importance of endurance limit in design of machine components?
The endurance limit helps to increase the life of the machine components for the fluctuating loading. Therefore the endurance limit has importance at the time of design of machine components.