The gear trains are expected to provide a high gear ratio within a limited space. The epicyclic gear train is the one that helps to provide a higher gear ratio (or speed ratio) within a small space. Thus in this article, we are discussing the epicyclic gear train in detail.
Contents:
What is Epicyclic gear train?
Epicyclic gear train is the type of gear train in which the axis of one or more gears (planet gears) revolves around the fixed axis of another gear (sun gear). This gear train is also known as a planetary gear train.
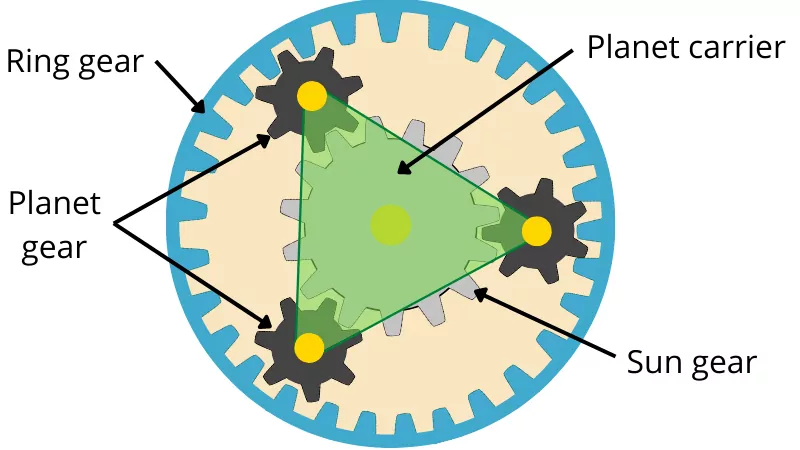
In this gear train, the central gear that has a fixed axis is known as the sun gear while the gears that revolve around the sun gear are known as planet gears.
The planet pinions mesh with the sun gear, thus these planet pinions revolve around their own axis as well as around the axis of the sun gear.
As shown in the above figure, the planet pinions are meshed with the sun gear as well as with the ring gears. The axel of the planet pinions is attached to the planet carrier; thus, the planet carrier also revolves around the sun gear along with planet gear.
As the number of planet pinions in the epicyclic gear train increases, the number of teeth that are involved simultaneously in a power transmission also increases. During such power transmission, the stress is shared among these teeth, and hence each tooth experiences less stress.
Therefore, the epicyclic gear train can transmit a high amount of power and torque with minimum stress on teeth.
The epicyclic gear train can obtain higher gear ratios within less space. Thus, it has a broad range of applications.
As this gear train requires two inputs for its proper functioning, thus the degree of freedom for the epicyclic gear train is two.
Compound epicyclic gear train:
This type of epicyclic gear train uses compound gear as planet gear.
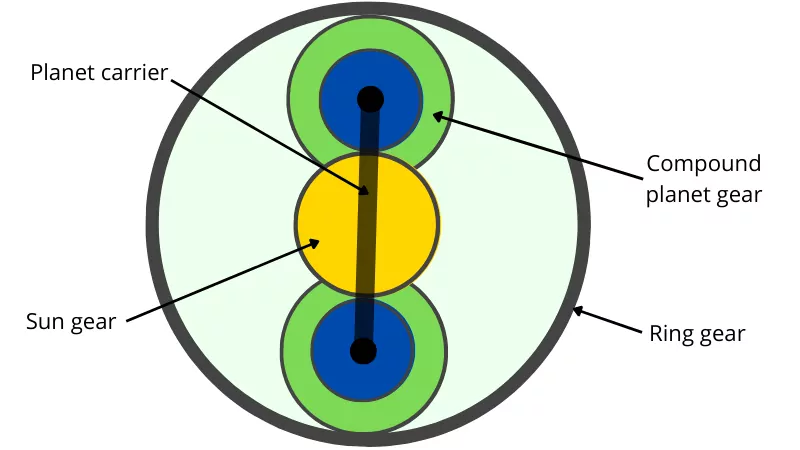
As shown in the above figure, one gear of the compound planet gear meshes with the sun gear, and another gear meshes with the ring gear.
The purpose of using compound planet gear is to increase the gear ratio of the epicyclic gear train.
Parts of epicyclic gear train:
The epicyclic gear train consists of the following important components.
1] Sun gear:
It is the middle gear of the epicyclic gear train with a fixed axis of rotation. The sun gear meshes with the planet pinions that revolve around the sun gear.
2] Planet gears:
The planet gears mesh between the sun gear and ring gear and revolve around their own axis and around the axis of the sun gear.
3] Planet carrier:
The planet carrier is connected to the axles of all planet gears. When the planet gears start to rotate around the sun gear, the planet carrier also revolves around the axis of the sun gear.
The planet carrier also performs a vital role to control the gear ratio of the epicyclic gear train.
4] Ring gear:
The ring gear or the annular ring is the ring with teeth on its inner race. The planet gears constantly mesh with the teeth of the ring gear.
How does an epicyclic gear train work?
The epicyclic gear train works in different configurations to obtain different gear ratios. It is achieved by fixing different components of the epicyclic gear train as follows:
a] Ring gear fixed:
In this condition, the ring gear is kept stationary while the sun gear acts as the driver and the planet carrier acts as a driven member.
This configuration of the epicyclic gear train gives the highest gear ratio. It helps to meet higher torque requirements at a lower speed.
b] Sun gear fixed:
In this case, the sun gear is kept stationary and power is supplied to the ring gear to drive the planet carrier. This configuration of the epicyclic gear train gives a comparatively lower gear ratio.
c] Planet carrier fixed:
In this case, the planet carrier is kept stationary, therefore the sun gear and the ring gear rotate in the opposite direction.
Hence this configuration of the epicyclic gear train is used to obtain reverse gear in the vehicle.
d] Planet gear fixed:
In this case, the planet gears are kept stationary, therefore it stops the relative motion in between its components, and thus the whole gear train rotates as a single unit.
How to find the gear ratio of epicyclic gear train?
In the epicyclic gear train, the different drives with different gear ratios are obtained by varying the driving and driven member. Following are the steps used to find the gear ratio for different configurations of the epicyclic gear train:
Consider the example below for an easy understanding of the steps.
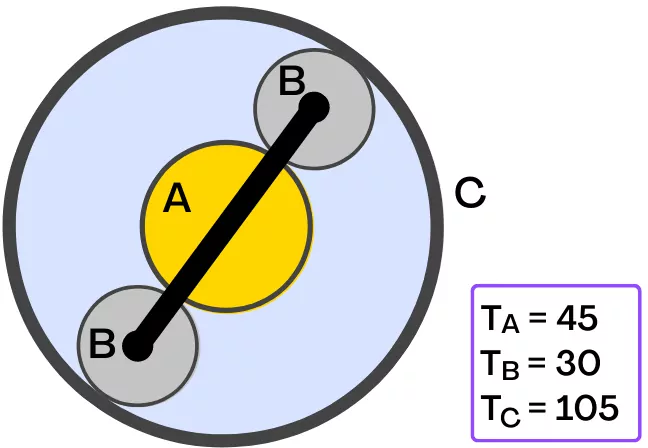
Step 1] Find the equation of motion for each component:
This can be found by using a tabular method as follows,
a) Consider the planet carrier is fixed so that the pinion gears don’t revolve around the sun gear and the gear train acts as a simple gear train.
Now by considering the sun gear is revolving at ‘x’ rpm, find the speed of each component and note it down in the table below.
For the above example, the speed of each component is noted in the table below.

b) Now consider the planet carrier is rotating at y rpm, therefore add y rpm to the speed of each component. For the above example, the table of motion becomes as follows,

From the above table, the equations of the speed of each component are as follows,
`N_{carrier}` = y
`N_{A} = x + y`
`N_{B} = -x.\frac{T_{A}}{T_{B}} + y`
`N_{C} = -x.\frac{T_{A}}{T_{C}} + y`
Step 2] Find gear ratio for different configurations:
By using the equation of speed, it is easy to find the gear ratio of different configurations.
For the above example, the gear ratio for the different configurations is as follows.
1] Sun- Input, Planet carrier- Output, Ring gear- Stationary:
As the ring gear is stationary,
`N_{\text{Ring}}` = `N_{C}` = 0
`-x.\frac{T_{A}}{T_{C}}` + y = 0
`-x.\frac{45}{105}` + y = 0
y = 0.428.𝑥
The gear ratio for the above configuration is given by,
i = `\frac{N_{\text{input (sun)}}}{N_{\text{output (carrier)}}}=\frac{N_{A}}{N_{\text{carrier}}}=\frac{x + y}{y}`
i = `\frac{x + (0.428x)}{0.428x}`
i = 3.336
2] Sun- stationary, Planet- output, Ring- input:
As the sun gear is stationary,
`N_{\text{sun}}` = `N_{A}` = 0
𝑥 + y = 0
y = -𝑥
The gear ratio for the above configuration is given by,
i = `\frac{N_{\text{input (ring)}}}{N_{output (carrier)}}=\frac{N_{C}}{N_{carrier}}=\frac{-x.\frac{T_{A}}{T_{C}} + y}{y}`
i = `\frac{-x.\frac{45}{105} + (-x)}{(-x)}`
i = 1.428
In this way by using the equation of motion, we can easily calculate the gear ratio for the different combinations.
Advantages:
Following are some of the advantages of the epicyclic gear train:
- A higher reduction ratio can be obtained within a compact space.
- Transmits higher torque
- Lighter than other gear trains
- It develops fewer vibrations.
- The input and output shafts are co-axial.
- Higher efficiency of transmission
- Quieter operation
Disadvantages:
Following are some of the disadvantages of the epicyclic gear train:
- Complex design and manufacturing
- It requires proper lubrication
- The shafts of the driving and driven equipment should be co-axial.
- High manufacturing cost.
Applications of the epicyclic gear train:
Following are some of the applications of the epicyclic gear train:
- Automobile transmission: The vehicles with the automatic transmission use an epicyclic gear train in the transmission unit.
- Wind turbine: The gearbox used in the wind turbine consists of an epicyclic gear train.
- Gearbox: The compact gearbox with a higher gear ratio uses an epicyclic gear train.
Solved Numericals:
1] The sun gear of the following epicyclic gear train is kept stationary while planet carrier is the driving member and ring is the driven member. If TA = 40, TB = TC = 15, then find,
a] No of teeth on the ring gear
b] Gear ratio
Solution:
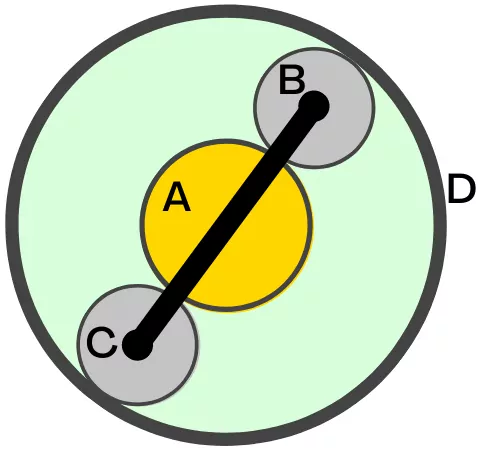
a] Number of teeth on ring gear, (TD):
From the above figure, the relation between pitch circle diameter of the gears is given by,
`d_{A}+d_{B}+d_{C}=d_{D}`
As, d = (Gear module × Number of teeth) = m × T, thus the above equation becomes,
`mT_{A}` + `mT_{B}` + `mT_{C}` = `mT_{D}`
`T_{A}` + `T_{B}` + `T_{C}` = `T_{D}`
By putting the values of the number of teeth,
40 +15 + 15 = TD
∴ TD = 70
Thus the ring gear has 70 teeth.
b] Gear ratio:
The table of motion to find the equation of motion is as follows,

From above table, the equation of speed of each component are as follows,
`N_{\text{carrier}}` = y
`N_{A}` = 𝑥 + y
`N_{C}` = `N_{B}` = `-x.\frac{T_{A}}{T_{B}}` + y
`N_{D}` = `-x.\frac{T_{A}}{T_{D}}` + y
As the sun gear is stationary,
∴ NA = 𝑥 + y = 0
∴ 𝑥 = – y
The gear ratio for the above gear train is given by,
i = `\frac{N_{\text{Input (carrier)}}}{N_{\text{Output (Ring)}}}` = `\frac{N_{\text{carrier}}}{N_{\text{D}}}`
i = `\frac{y}{-x\frac{T_{A}}{T_{D}}+y}`
Put 𝑥 = – y in above equations,
i = `\frac{y}{-(-y)\frac{40}{70}+y}`
i = 0.636
2] In the given compound epicyclic gear train, if the planet carrier is kept stationary and the sun gear is rotating at 900 rpm, then find the speed of rotation of ring gear.
Data: TA = 25, TB = 20, TC = 25, TD = 70
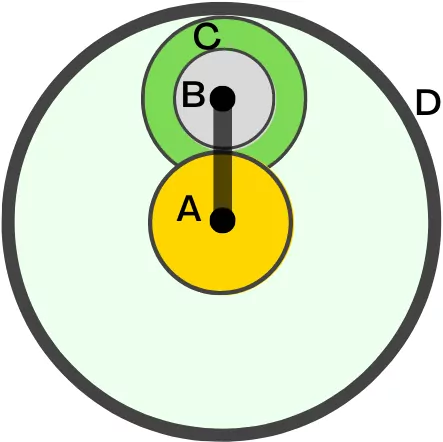
Solution:
The table of motion for the above compound epicyclic gear train is shown below,

From above table of motion, the equations for the speed of each gear are as follows,
`N_{\text{carrier}}=y\cdots[1]`
`N_{A}=\text{𝑥 + y}\cdots[2]`
`N_{B}` = `N_{C}` = `-x.\frac{T_{A}}{T_{B}}+y\cdots[3]`
`N_{D}` = `-x.\frac{T_{A}}{T_{B}}.\frac{T_{C}}{T_{D}}+y\cdots[4]`
The planet carrier is kept stationary.
∴ `N_{\text{carrier}}` = y = 0
∴ y = 0
Put this value in equation [2]
`N_{A}` = 𝑥 + y
900 = 𝑥 + 0
∴ 𝑥 = 900
Now put these values in equation [4]
`N_{D}` = `-x.\frac{T_{A}}{T_{B}}.\frac{T_{C}}{T_{D}}` + y
`N_{D}` = -(900).`\frac{25}{20}.\frac{25}{70}` + 0
ND = – 401.78 rpm
Therefore the ring gear rotates at 401.78 rpm in opposite direction of sun gear.
FAQs:
-
How many DOF epicyclic gear train has?
For the epicyclic gear train, the degree of freedom (DOF) is 2.
-
What are the various types of the torque in an epicyclic gear train?
The various types of torque in the epicyclic gear trains are driving torque, driven torque, and holding/braking torque.
-
What is holding torque in epicyclic gear train?
The torque required to hold the ring gear stationary is known as the holding torque in an epicyclic gear train.
The epicyclic gear train is now used in various applications due to its unique characteristics. We hope you found the above information useful in understanding the planetary gear train.
Peoples also like to read: