When we release any object from a height, it gets accelerated toward the floor. Even if we never applied any force, the object continuously accelerated toward the floor. In this case, the force acting on the object is the gravitational force and the acceleration caused by the object is the gravitational acceleration.
In this article, we will discuss gravitational acceleration in great detail.
Contents:
What is Gravitational acceleration?
Gravitational acceleration is the acceleration caused in an object during the free fall due to the sole effect of the gravitational force of attraction. It is also referred as acceleration due to gravity.
The term acceleration indicates the change in the velocity of the body. The body generally accelerates due to the application of force. Gravity indicates the force of attraction between any massive bodies.
Thus gravitational acceleration indicates acceleration occurs in the body due to the influence of the gravitational force.
Eg. A below figure-A shows the ball falling from the top of the building, in this case, the force acting on the ball is the gravitational force, and acceleration in the ball is equal to the gravitational acceleration.
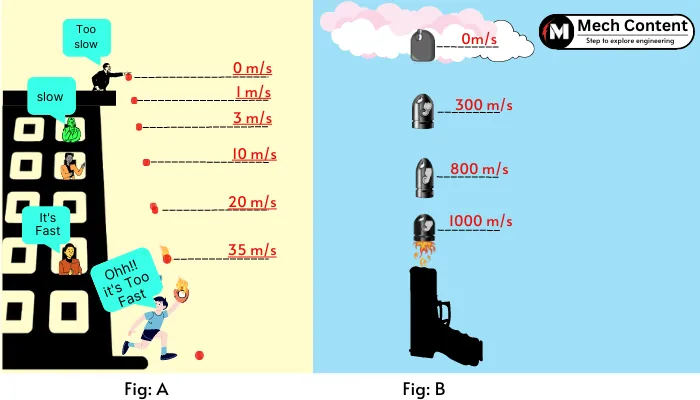
Similarly, the figure-B shows the deceleration in the bullet fired in the air. Here the gravitational force opposes the motion of the bullet with the deceleration equal to the gravitational acceleration.
Gravitational acceleration is denoted by the symbol ‘g’. As it is an acceleration, thus it has a SI unit of m/s2 and an FPS unit of ft/s2.
The average value of gravitational acceleration near the surface of the earth due to the earth’s gravitational force is 9.81 m/s2 or 32.2 ft/s2.
To know how Gravitational Acceleration is different from Gravitational Force, then check out this published post.
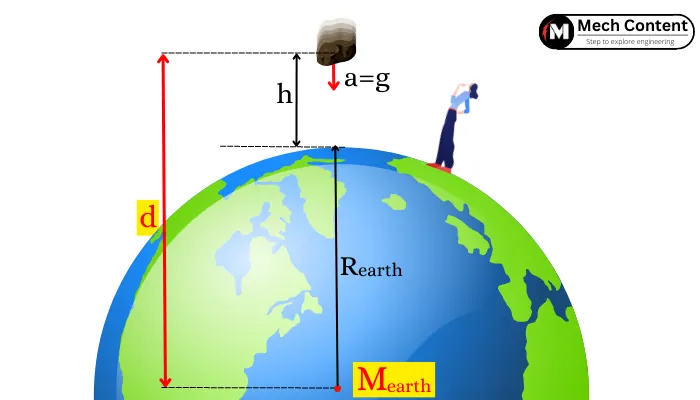
The gravitational acceleration acting on any object on the planet is directly proportional to the mass of the planet and inversely proportional to the square of the distance (d) between the center of mass of the planet and the respective body.
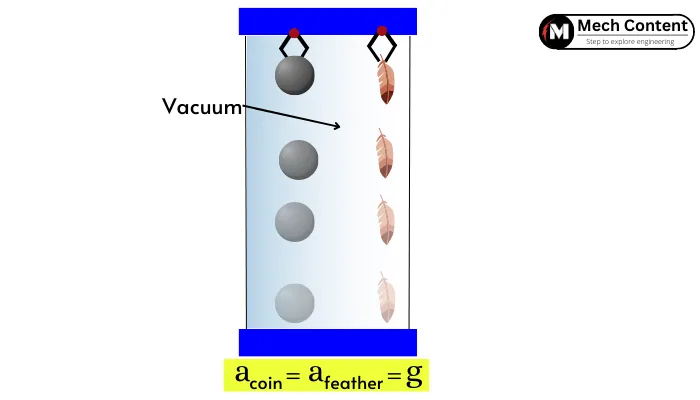
The gravitational acceleration is irrespective of the mass of the falling body, i.e. the value of gravitational acceleration never depends on the mass of the object, it is same for the all objects.
In the coin feather experiment, the feather and coin are released at the same instance in an evacuated tube. Due to the lack of air resistance, the feather also falls at the same rate as the coin and reaches the bottom at the same time. It shows that the acceleration due to gravity is the same for all masses.
Following are values of gravitational acceleration near the surface of some of the planets/stars.
| Planet/ Star | g (m/s2) |
|---|---|
| Mars | 3.7 |
| Earth | 9.81 |
| Moon | 1.6 |
| Sun | 275 |
Table Source: Space NSS
Gravitational acceleration equation:
The gravitational acceleration near the surface (g) is given by,
`g =\frac{GM}{R^{2}}`
Where,
G = Gravitational constant = 6.67 × 10-11 m3/Kg.s2
M = Mass of the planet/star
R = Radius of planet/star
The gravitational acceleration at height ‘h’ above the surface is given by,
`g_{height} =\frac{GM}{(R+h)^{2}}`
OR
`g_{height} =g.[1 + \frac{h}{R}]^{-2}`
Where,
g = Gravitational acceleration near the surface
The gravitational acceleration at the depth ‘𝑎’ below the surface is given by,
`g_{depth} =g.[1 – \frac{a}{R}]`
Derivation:
a] Gravitational acceleration on the surface:-
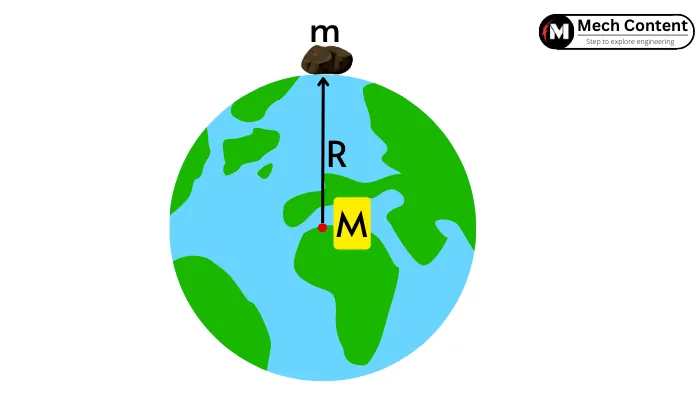
As per newtons law of gravitation, the force of attraction between two masses is given by,
`F =\frac{GMm}{d^{2}}`
Where,
G = Gravitational constant
M = Mass of the larger body (e.g. earth, moon, etc.)
m = Mass of a smaller body (e.g. stone, ball, etc.)
d = Distance between the center of mass
In case, one of the body is very small in comparison with the other,
d = R = radius of the larger body
Thus the force of gravitation becomes,
`F_{gravitational} =\frac{GMm}{R^{2}}\cdots[1]`
As per newtons second law, the acceleration is given by,
Gravitational acceleration on a smaller body, (g) = `\frac{F_{\text{gravitational}}}{\text{mass of small body}}`
Putting Fgravitational from equation [1],
`g =\frac{ \frac{GMm}{R^{2}}}{m}`
`g = \frac{GM}{R^{2}}`
This is the formula to find the Gravitational acceleration on the surface of the body.
b] Gravitational acceleration below the surface:-
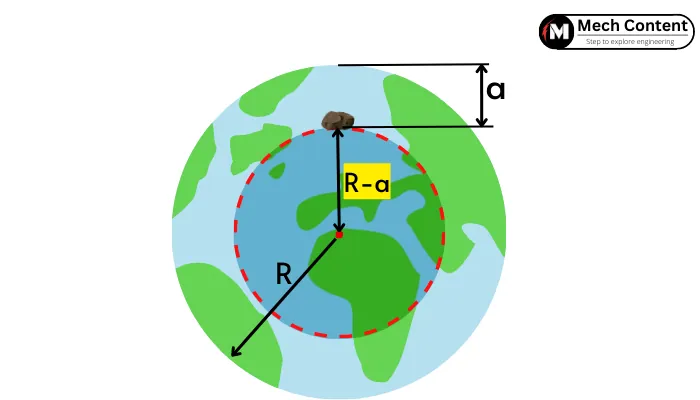
Consider the object is at depth of ‘𝑎’ from the surface. The gravitational force acting on an object below the surface is given by,
`F =\frac{GM’m}{d^{2}}`
and the ‘g’ is given by,
`g_{depth} =\frac{F}{m} = \frac{GM’}{d^{2}}`
Where, M’ = mass of inner sphere = ρ. vinner sphere =`\rho.\frac{4}{3}.\pi(R-a)^{3}` and d = [R – a].
`\therefore g_{depth} =\frac{G}{[R – a]^{2}}. [\rho.\frac{4}{3}.\pi(R-a)^{3}]`
`g_{depth} =\frac{G}{[R – a]^{2}}. [\rho.\frac{4}{3}.\pi.R^{3} \times \frac{(R-a)^{3}}{R^{3}}]`
As, `\rho.\frac{4}{3}.\pi.R^{3}` = M = total mass,
`\therefore g_{depth} =\frac{G}{[R – a]^{2}}. [M \times \frac{(R-a)^{3}}{R^{3}}]`
`g_{depth} =\frac{G.M}{R^{3}}.[R – a]`
`g_{depth} =\frac{G.M}{R^{2}}.\frac{R – a}{R}`
As `\frac{G.M}{R^{2}}` = g (gravitational acceleration on surface),
`\therefore g_{depth} =g.[1 – \frac{a}{R}]`
c] Gravitational acceleration above the surface:-
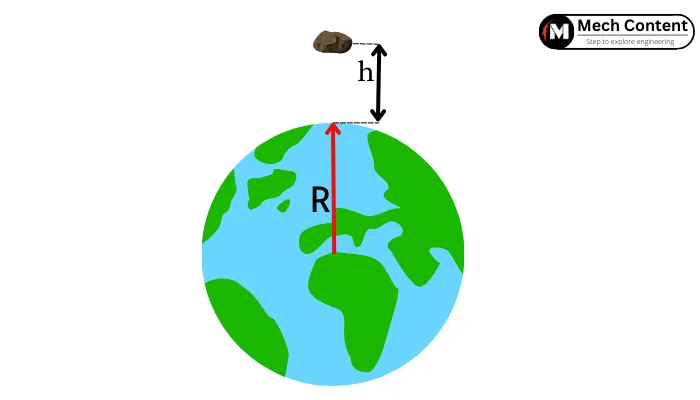
The gravitational force acting on the object at an elevation of ‘h’ above the surface is given by,
`F =\frac{G.M.m}{d^{2}}`
As d = R + h
`\therefore F =\frac{G.M.m}{[R + h]^{2}}`
The ‘g’ on an object of mass ‘m’ is given by,
`g_{height} =\frac{F}{m} = \frac{G.M}{[R + h]^{2}}`
`g_{height} =\frac{G.M}{R^{2}}.\frac{R^{2}}{[R + h]^{2}}`
As `\frac{G.M}{R^{2}}= g` (gravitational acceleration on surface),
`g_{height} =g.\frac{R^{2}}{[R + h]^{2}}`
`g_{height} =g.[1 + \frac{h}{R}]^{-2}`
Factors affecting gravitational acceleration:
The following are the factors that affect acceleration due to gravity:-
1] Rotational speed: The rotational motion of the earth causes centrifugal force. As it acts away from the center, it has a slight effect on gravitational acceleration.
The amount of centrifugal force is maximum at the equator and zero at the poles. It is one of the reasons why gravitational acceleration is less at the equator and high at the poles.
2] Shape: The acceleration due to gravity is higher where the distance from the center of mass (radius) is less and it is less where the distance from the center of mass (radius) is large.
Due to the bulging at the equator, the earth has a higher radius at the equator and less at the poles. Thus at the equator, the gravitational acceleration is slightly less than at the poles.
3] Distance from the surface: The gravitational acceleration is inversely proportional to the square of the distance between the center of masses. Thus the gravitational acceleration acting on the falling object increases with an increase in elevation from the earth.
But, acceleration due to gravity decreases as we move below the earth’s surface.
Examples with answers:
1] Find the acceleration due to gravity at an altitude of 3000 Km above the earth’s surface. (Assume, Mearth = 5.9722 × 1024 Kg, Rearth = 6378 Km, G = 6.67 × 10-11 m3/Kg.s2).
Given:
h = 3000 Km = 3000 × 103 m
Mearth = 5.9722 × 1024 Kg
Rearth = 6378 Km = 6378 × 103 m
G = 6.67 × 10-11 m3/Kg.s2
Solution:-
The value of ‘g’ above the earth’s surface is given by,
`g=\frac{GM}{(R + h)^{2}}`
`g =\frac{(6.67 × 10^{-11}) \times (5.9722 × 10^{24})}{((6378 × 10^{3}) + (3000 × 10^{3}))^{2}}`
g = 4.529 m/s2
2] Based on the following data, find the gravitational acceleration on the surface of the moon and mars.
Mmoon = 7.347 × 1022 Kg, Rmoon = 1740 Km, Mmars = 6.39 × 1023 Kg, Rmars = 3,389.5 km
Given:
Mmoon = 7.347 × 1022 Kg
Rmoon = 1740 Km = 1740 × 103 m
Mmars = 6.39 × 1023 Kg
Rmars = 3,389.5 km = 3389.5 × 103 m
Solution:-
a] Gravitational acceleration on the moon’s surface:
The acceleration due to gravity on the moon’s surface is given by,
`g =\frac{GM}{R^{2}}`
`g =\frac{(6.67 × 10^{-11}) \times (7.347 × 10^{22})}{(1740 × 10^{3})^2}`
gmoon = 1.61 m/s2
b] Gravitational acceleration on the surface of mars:
The acceleration due to gravity on the surface of mars is given by,
`g =\frac{GM}{R^{2}}`
`g =\frac{(6.67 × 10^{-11}) \times (6.39 × 10^{23})}{(3389.5 × 10^{3})^2}`
gMars = 3.71 m/s2
FAQs:
-
What causes Gravitational acceleration?
The gravitational force acting on the object causes acceleration due to gravity in the object.
-
Where earth has maximum Acceleration due to gravity?
The earth has maximum acceleration due to gravity on the poles.
-
Is the Earth’s gravitational acceleration constant?
Gravitational accelerations changes with change in location and altitude.
-
When does Gravitational acceleration consider negative?
The gravitational acceleration is considered negative when the object is moving in an upward direction.
-
When should Acceleration due to gravity be used?
Acceleration due to gravity is used while the free fall of the object under the gravitational field of the planet.
-
How Gravitational acceleration and gravity are different?
Gravity indicates the gravitational force of attraction while acceleration due to gravity is the acceleration caused by gravitational force or gravity.