Contents:
What is Hydrodynamic boundary layer?
When the free stream of fluid with the constant free stream velocity of `u_{\infty}` approaches toward the stationary surface then due to the resistance offered by a stationary plate and viscosity of the fluid, the velocity gradient (du/dy) is generated in the fluid.
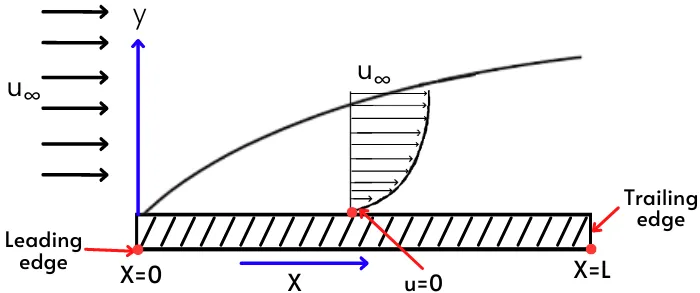
Therefore, the Hydrodynamic boundary layer is the region in the fluid flow where the velocity gradient is present in the direction perpendicular to the direction of the free stream.
While the region outside of the boundary layer is known as the outer flow region where the velocity of the fluid is equal to the free stream velocity.
What is laminar boundary layer?
The laminar boundary layer is the region of the boundary layer in which the fluid flow takes place in a laminar manner. The flow of fluid in the laminar boundary layer takes place in the form of layers.
The motion of each layer in the laminar boundary layer region is affected by the cohesive force between its adjacent layers.
It is considered that the laminar boundary layer exists till the Reynolds number reaches up to `5\times 10^{5}`.
Velocity profile in laminar boundary layer flow:
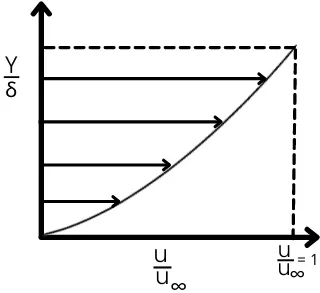
The velocity profile in laminar boundary layer flow is considered as parabolic in nature.
The above figure shows the variation of `\frac{u}{u_{\infty}}` ratio with respect to change in `\frac{y}{\delta}`.
Here,
u = Velocity of the fluid at different layers
δ = Boundary layer thickness (Distance from u = 0 to u = `u_{\infty}`)
y = Perpendicular height from the plate surface
`u_{\infty}` = Free stream velocity
The equation of the velocity profile for laminar flow is given by,
`\frac{u}{u_{\infty}}=2(\frac{y}{\delta})-(\frac{y}{\delta})^{2}`
Reynolds number for laminar boundary layer:
The Reynolds number for the boundary layer over a flat plate is given by,
`R_{ex}=\frac{\rho. u.x}{\mu}`
Where x is the distance over a flat plate and the value of Re increases with an increase in the length of a plate.
From this equation, it is clear that the Reynolds number is maximum at a distance x = L.
therefore maximum Reynolds number over a flat plate is,
`R_{eL}=\frac{\rho. u.L}{\mu}`
Critical Reynolds number: It is the Reynolds number at which the laminar flow becomes turbulent.
The value of the critical Reynolds number is considered as `R_{ex}`= `5\times 10^{5}`
It means that the laminar nature of the boundary layer ends at `R_{ex}`= `5\times 10^{5}`.
Boundary conditions:
1) When the free stream fluid touches the plate, the free stream has a velocity of `u_{\infty}` therefore at x = 0 (leading edge), the velocity gradient `\frac{du}{dy}` is equal to the zero at y = 0. Therefore boundary layer thickness at x = 0 is also equal to zero.
∴ At x = 0, δ = 0
2) The layer of fluid adjacent to the flat surface (at y = 0) has a velocity equal to zero due to the no-slip condition.
∴ At y = 0, u = 0
3) At the height of boundary layer thickness (δ), the velocity of the fluid becomes almost equal to the free stream velocity `u_{\infty}`.
∴ At y = δ, u = `u_{\infty}`
Therefore we can also say that, at y = δ, the velocity gradient also becomes zero.
∴ At y = δ, `\frac{du}{dy}` = 0
4) The boundary layer thickness increases with an increase in the length of contacting surface (x) due to the increase in retardation of fluid in the X-direction.
Therefore the value of boundary layer thickness is maximum at the end of the surface of the plate (Trailing edge).
∴ At x = L, `δ` = `\delta _{\text{max}}`
What is Hydrodynamic boundary layer thickness?
Boundary layer thickness is the perpendicular distance between the surface of the plate and the point in a fluid at which the velocity of the fluid becomes equal to the free stream velocity.
It is also defined as the normal distance from the plate surface at which the velocity of the fluid equals to 99% of free stream velocity.
The boundary layer thickness is measured perpendicular to the surface from the fluid velocity of u = 0 to u = `u_{\infty}`
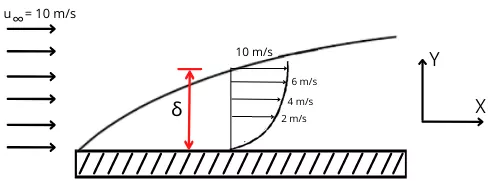
Example:- As shown in the figure, the velocity of the fluid particle at y = δ becomes equal to the `u_{\infty}`. Therefore δ is the boundary layer thickness at the particular cross-section.
Hydrodynamic boundary layer displacement thickness:
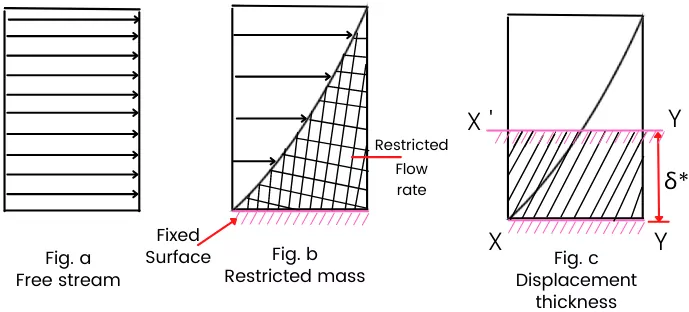
Figure-a shows the flow of the free-stream which is in unrestricted condition and figure-b shows the restricted flow rate of the free stream due to the boundary layer generation.
Now, the concept of displacement thickness says that,
If we hypothetically raise the position of the plate surface from xy to x’y’ by distance δ, then the flow rate restricted in this case is equal to the flow rate restricted by parabolic boundary layer generation. Therefore for the `\delta^{\star}`, the restricted flow rate in figure b and in figure c are equal.
Therefore the displacement thickness is the distance by which if we raise the position of the surface plate then the flow rate restricted is equal to the flow rate restricted due to the boundary layer generation.
The displacement thickness is given by,
`\delta^{\star}`=`\int_{0}^{\delta}[1-\frac{u}{u_{\infty}}].dy`
Momentum thickness (θ):
Momentum thickness is the distance by which if we raise the position of the surface plate then the momentum restricted by this action is equal to the momentum restricted due to the boundary layer generation.
The momentum thickness is given by,
θ =`\int_{0}^{\delta}\frac{u}{u_{\infty}}[1-\frac{u}{u_{\infty}}].dy`
Characteristics of boundary layer thickness:
The hydrodynamic boundary layer thickness has the following characteristics:-
1) The boundary layer thickness is zero at the leading edge of the plate.
2) The boundary layer thickness is maximum at the trailing edge.
3) The thickness of the boundary layer decreases with an increase in free stream velocity.
4) The thickness of the boundary layer increases with an increase in viscosity.
Why thickness of boundary layer increases?
While moving on the plate surface, the liquid molecules continuously retards due to the resistance offered by the plate surface (no-slip condition).
This retarded fluid molecule tries to retard the molecules in the upper layer due to the cohesive force between them.
Therefore as the fluid advances over the plate surface, the retardation of fluid layers also increases, and hence the height of the fluid layer for maximum velocity also increases.
Therefore the thickness of the boundary layer increases in a downstream direction.
FAQ’s
-
What is hydrodynamic boundary layer?
The hydrodynamic boundary layer is the region in the fluid flow where the velocity gradient is present in the direction perpendicular to the direction of the free stream.
-
What do you mean by hydrodynamic and thermal boundary layer?
For the free stream of the fluid passing over the solid surface with different velocities, the hydrodynamic boundary layer is the region near the surface where the velocity gradient is present.
For the fluid flowing over the solid surface with different temperatures, the thermal boundary layer is the region near the surface where the temperature gradient is present. -
What is difference between thermal boundary layer and hydrodynamic boundary layer?
The difference between hydrodynamic and thermal boundary layers is that the hydrodynamic boundary layer has a region with a velocity gradient and the thermal boundary layer has a region with a temperature gradient.
-
What is the importance of hydrodynamic and thermal boundary layers in heat transfer?
The hydrodynamic and thermal boundary layer in heat transfer is necessary to determine the heat transfer between fluid flow and the surface of the body in contact with the fluid.