A simple pendulum consists of a bob of mass ‘m’ attached to one end of the string while another end of the string is tied to the fixed support. When the bob of the pendulum gets displaced from its equilibrium position, the restoring force generated due to the gravitational force causes the pendulum to oscillate about the equilibrium position.
In this article, we will look at the kinetic and potential energy that the pendulum possesses during its oscillatory motion.
The pendulum possesses potential energy due to its elevation from the equilibrium position while it possesses kinetic energy due to the tangential velocity of the bob.
The constantly changing elevation of the bob from its equilibrium position constantly changes the potential energy and kinetic energy of the pendulum.
Let’s go through each one in detail.
Contents:
Potential energy of a pendulum:
As discussed above the potential energy of a pendulum depends on the elevation of a the bob from its equilibrium position and the mass of the bob. but as the mass of the bob is a constant quantity, the potential energy of the object is affected only by the elevation of the bob (`y`) from the equilibrium position.
The formula of the potential energy of the pendulum is given by,
P = mgy
Where,
m = Mass of the bob
g = Gravitational acceleration
y = Elevation of the bob
Hence at the equilibrium position (`y=0`), the bob has zero potential energy and when the bob is at its extreme position (`y=h_{max}`), the pendulum possesses maximum potential energy.
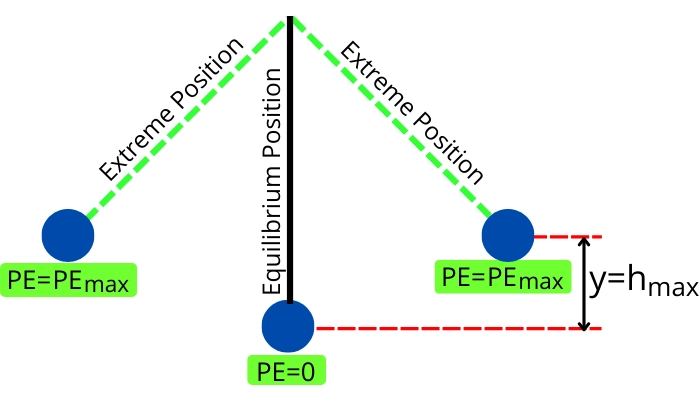
Thus we can say that,
At `y=0 \to PE = 0`
At `y=h_{max} \to PE=PE_{max}`
The below figure shows the different positions of the pendulum during its swing.
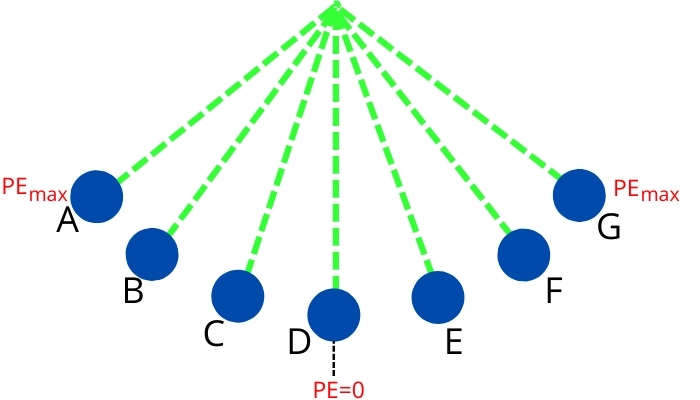
The potential energies of the pendulum for the different positions shown in the above figure can be compared as follows,
`PE_{A}>PE_{B}>PE_{C}>PE_{D}` and `PE_{D}<PE_{E}<PE_{F}<PE_{G}`
Potential energy based on the angle of swing:-
Let’s find the potential energy of the pendulum at the intermediate positions inclined at angle θ from the equilibrium position.
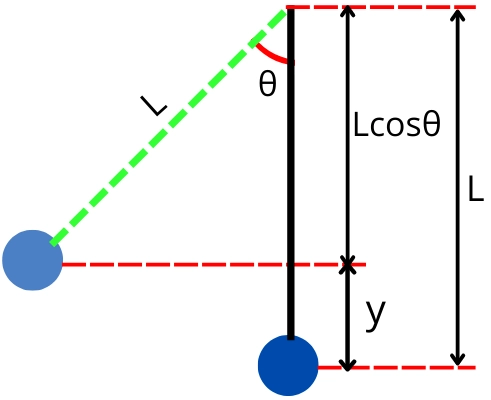
As shown in the figure, when the pendulum is inclined at an angle θ, the elevation of the bob from the equilibrium position is given by,
`y=L-Lcos\theta`
Thus the potential energy of a pendulum is given by,
`PE=mgy`
`PE=mg(L-Lcos\theta)`
`PE=mgL(1-cos\theta)`
The above equation gives the potential energy of a pendulum at different values of θ ranging from 0 to `\theta_{\text{max}}`.
Kinetic energy of a pendulum:
For the pendulum of mass of bob ‘m’, moving with a tangential velocity of ‘v’, the kinetic energy is given by,
`KE=\frac{1}{2}m.v^{2}`
But as the mass of the bob is a constant quantity thus the kinetic energy of the pendulum totally depends on a velocity of a bob.
Therefore the kinetic energy of the pendulum becomes maximum when the velocity of the bob becomes maximum and it becomes zero when the velocity of the bob becomes zero.
Kinetic energy based on the elevation of bob:-
Let’s find the relation between the elevation of the bob and its kinetic energy.
Consider there is no air resistance acting on the oscillating pendulum. Thus by the law of energy conservation, the total energy of the bob during the oscillation remains constant which is given by,
Total energy (TE) = Potential energy (PE) + Kinetic energy (KE)
`\therefore KE=TE-PE \cdots \cdots\text{Equation (1)}`
At the extreme positions, the velocity of the bob becomes zero, which means that the bob has zero kinetic energy at the extreme position while the potential energy reaches its maximum extent.
Thus at this position, the total energy of the bob is given by,
`TE=PE_{\text{max}}+0`
`\therefore TE=PE_{\text{max}}=mgh_{\text{max}}`
Where `h_{\text{max}}` indicates the maximum elevation of the bob (`y`) during a swing.
Now by putting the value of total energy (TE) in the above equation (1) of kinetic energy, we get,
`KE=mgh_{\text{max}}-\text{PE}`
`KE=mgh_{\text{max}}-mgy \cdots \cdots[\because PE=mgy]`
`\therefore KE=mg[h_{\text{max}}-y] \cdots \cdots\text{Equation (2)}`
From the above equation, we can say that the pendulum has maximum kinetic energy at its equilibrium position (`y=0`), and it has minimum kinetic energy at extreme positions (`y=h_{\text{max}}`).
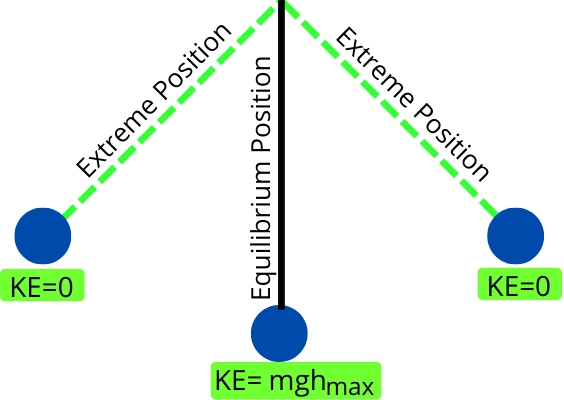
Hence,
`\text{At equilibrium position} (y=0), \to \text{KE}=mgh_{\text{max}}`
`\text{At extreme position} (y=h_{\text{max}}), \to \text{KE}=0`
The relation between the elevation of the bob and kinetic energy can be easily understood by the use of the following figure, which shows the different positions of the bob during its swing.
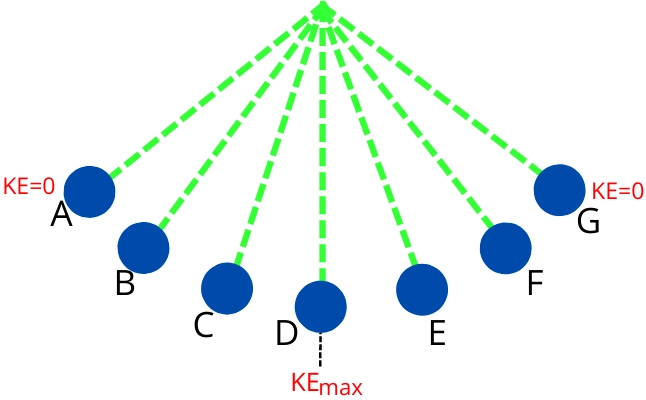
The relation between the kinetic energy of the pendulum at different positions can be compared as follows,
`KE_{A}<KE_{B}<KE_{C}<KE_{D}`
And
`KE_{G}<KE_{F}<KE_{E}<KE_{D}`
The pendulum in the above figure has zero kinetic energy at extreme positions A and G while it has maximum kinetic energy at equilibrium position D.
Relation between kinetic energy and angle of swing (θ):-
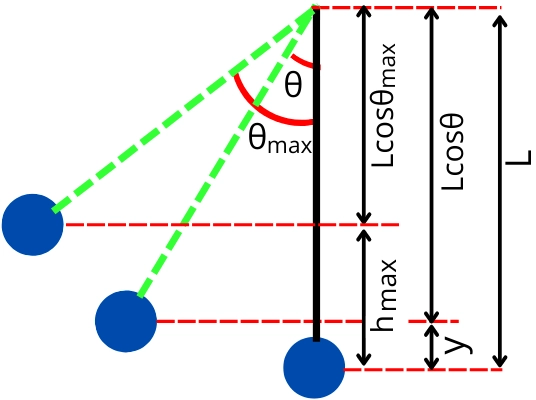
The elevation of bob (y) when the pendulum at angle θ from euilibrium position is given by,
`y=L(1-Cos\theta)`
Similarly, when the pendulum is at its extreme position `\theta_{max}`, the elevation of bob `h_{\text{max}}` is given by,
`h_{\text{max}}=L(1-cos\theta_{max})`
By putting these values in the above equation [2], we get
`KE=mg[h_{\text{max}}-y]`
`KE=mg[L(1-cos\theta_{max})-L(1-cos\theta)]`
`KE=mgL[cos\theta-cos\theta_{max}]`
The above equation helps to find the kinetic energy of the pendulum based on the angle made by the pendulum with respect to an equilibrium position.
Total energy of pendulum:
The total energy of the pendulum is the sum of the potential energy and kinetic energy at a specific location.
TE = PE + KE
If the air resistance acting on the pendulum is considered negligible then the total energy of the pendulum remains constant at different positions during the oscillation.
The total energy is generally equal to the potential energy at the extreme position or equal to the kinetic energy at the equilibrium position.
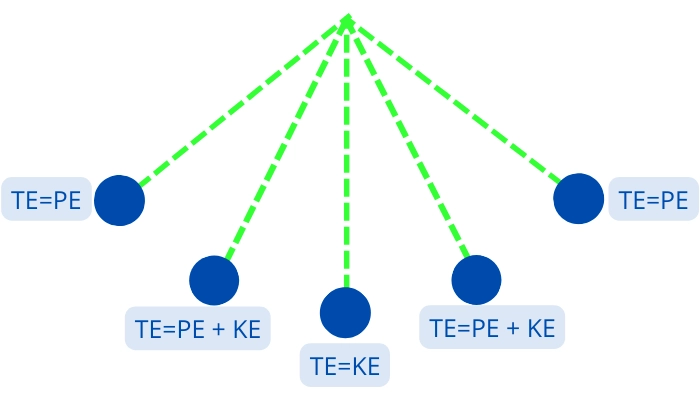
The above figure shows the total energy of the pendulum at a different position.
The potential energy, kinetic energy, and total energy of the pendulum at different positions are summarized in the below table.
| Position | Potential energy | Kinetic energy | Total energy |
|---|---|---|---|
| Equilibrium | 0 | `mgh_{\text{max}}` | `mgh_{\text{max}}` |
| Intermediate | `\text{mgy}` | `mg[h_{\text{max}}-y]` | `mgh_{\text{max}}` |
| Extreme | `mgh_{\text{max}}` | 0 | `mgh_{\text{max}}` |
Solved numericals:
1] Consider the pendulum has a length of 1 m and the bob of the pendulum has a mass of 150 grams. If the pendulum is released from the height of 100 mm, find the maximum kinetic energy of the pendulum.
Given:
L = 1 m
`h_{max}` = 100 mm = 0.1 m
m = 150 grams = 0.15 Kg
Solution:-
The pendulum has maximum kinetic energy at the equilibrium position, which is given by,
`KE_{max}=mgh_{\text{max}}`
`KE_{max}=0.15 \times 9.81 \times 0.1`
`\mathbf{KE_{max}}` = 0.147 J
2] If the kinetic energy of the pendulum at the height of 0.05 m is equal to the potential energy of the pendulum at an angle of 25 degrees from the equilibrium position, thus find the maximum elevation of the bob during its swing. Assume the pendulum has a mass of 350 grams and a length of 1.2 m.
Given:
m = 350 grams = 0.35 Kg
L = 1.2 m
`y_{1}` = 0.05 m
`\theta_{2}` = 25°
Solution:-
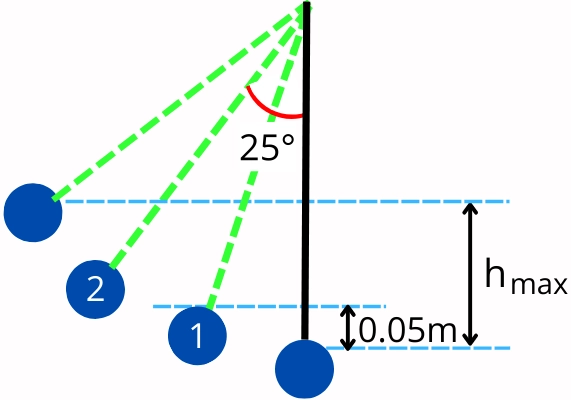
The kinetic energy of the pendulum at position 1 is given by,
`KE_{1}=mg[h_{\text{max}}-y_{1}]`
`KE_{1}=0.35 \times 9.81\times [h_{\text{max}}-0.05]`
`KE_{1}=3.4335 \times [h_{\text{max}}-0.05]`
The potential energy of the pendulum at position 2 is given by,
`PE_{2}=mgL(1-cos\theta_{2})`
`PE_{2}=0.35 \times 9.81 \times 1.2 \times (1-cos(25))`
`PE_{2}=0.386` J
As per the problem statement,
`KE_{1}=PE_{2}`
`3.4335 \times [h_{\text{max}}-0.05]=0.386`
`\mathbf{h_{\text{max}}}` = 0.162 m
This is the maximum elevation of the bob during its swing.
FAQs:
-
What relationship existed between kinetic and potential energy in a pendulum?
The relation between the potential energy (PE) and kinetic energy (KE) of the pendulum is given by,
PE + KE = Constant = Total energy of pendulum. -
Where do kinetic and potential energy in a pendulum equal each other?
At half of the maximum elevation of the bob (y = h/2), the potential and kinetic energy of the pendulum become equal.
-
How does the kinetic energy of a pendulum change into potential energy?
As the bob of the pendulum rises above from the equilibrium position, the kinetic energy of the pendulum gets converted into the gravitational potential energy (potential energy).
-
When does the pendulum acquire potential energy?
The pendulum possesses the potential energy when it is elevated above the equilibrium position.
-
Where does a pendulum’s potential energy reach its peak?
The potential energy of the pendulum becomes greatest at the extreme position (farthest position from the equilibrium position).
-
Does a pendulum in motion have potential energy?
The moving pendulum has both potential and kinetic energy.
-
What is the pendulum’s maximum kinetic energy?
The maximum kinetic energy of the pendulum is given by,
KEₘₐₓ = mghₘₐₓ
Where,
m = mass of pendulum bob
hₘₐₓ = maximum elevation of bob. -
What factors influence a pendulum’s kinetic energy?
The kinetic energy of the pendulum is affected by the following factors,
Mass of the bob
Angular displacement
Length of the string. -
Is the kinetic energy of a pendulum affected by its length?
As the length of the pendulum increases, the elevation of the bob for the same displacement of the bob decreases. This lowers the maximum potential energy and thus it affects the kinetic energy.
Friends we have covered a lot of information regarding the Kinetic and Potential energy of Pendulum. We hope we answered all of your questions about that topic.
Read here: