Newton’s law of viscosity: Definition, Types of fluids, Significance

If we pour a cup of water over an inclined surface while also pouring a cup of honey onto the same inclined surface, the water will undoubtedly flow quicker than the honey. This occurs because of the property of fluid known as viscosity. In this article, we are going to discuss the law associated with fluid viscosity which is known as Newton’s law of viscosity.

What is newton’s law of viscosity?

Newton’s law of viscosity says that for the moving fluid, the shear stress is directly proportional to the rate of shear strain.

Mathematically it is expressed as,

`\tau ∝ \frac{du}{dy}`

`\tau` ∝ μ(`\frac{du}{dy}`)

Where,
`\tau` = Shear stress in fluid
`\frac{du}{dy}` = Rate of shear strain (Velocity gradient)
μ = Dynamic viscosity of fluid

Terms related to Newton’s law of viscosity:

To know about newton’s law of viscosity in a better way, it is necessary to know about the terms like fluid viscosity, shear stress, and shear strain in fluids.

Viscosity:-

Viscosity is the property of fluid by virtue of which any layer in fluid opposes the motion of its adjacent layers.

Example:-

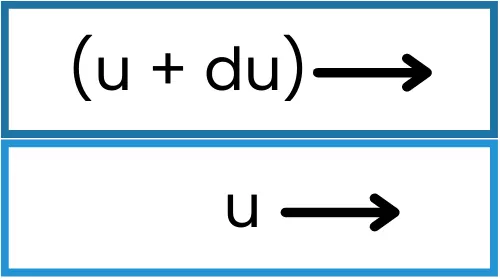
The above figure shows two adjacent fluid layers, out of them the lower layer is moving with a velocity of ‘u’ and the upper layer is moving with a relatively higher velocity of (u + du).

Thus because of the viscosity, the lower layer tries to retard the upper adjacent layer and the upper layer tries to accelerate the lower layer.

Shear stress (𝜏):-

Because of the viscosity of the fluid and the difference in velocity between adjacent layers, the shear stress is developed between the adjacent layers.

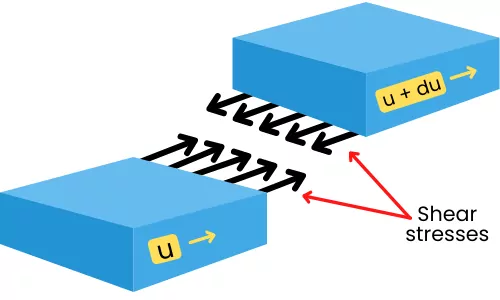
As shown in the above figure, the upper layer is under shear stress because of the resistance offered by its adjacent lower layer. Similarly, the lower layer is under shear stress due to the resistance created by the adjacent upper layer.

Rate of shear strain:-

Consider a smaller portion of the fluid of smaller height ‘dy’ flowing over stationary plates as shown in figure-A. Assume the smaller portion of the fluid is consists of a number of elemental layers as shown in the figure.

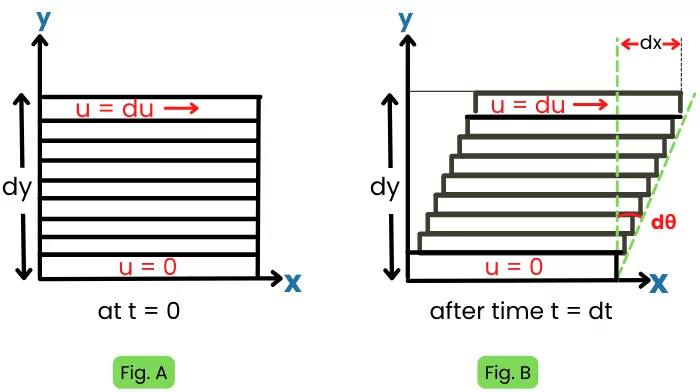
The lowest layer of fluid that is in contact with the stationary plate has a velocity of u = 0 and the uppermost layer of fluid is moving with the velocity of du.

The above figure-A shows the position of layers at time t = 0 and figure B shows the position of elemental layers after the time interval of ‘dt’.

After a time interval of ‘dt’, the upper layer of fluid gets displaced by distance dx.
Thus the shear strain for this smaller portion of the liquid is given by,

Shear strain = tan(dθ) = `\frac{dx}{dy}`

For the smaller value of dθ, tan(dθ) = dθ

Thus the equation becomes,

dθ = `\frac{dx}{dy}`

As the upper layer is moving at speed of du. Thus the distance covered by the upper layer (dx) is given by,

dx = du.dt

Put the value of dx in the equation of dθ.

dθ = `\frac{du.dt}{dy}`

`\frac{dθ}{dt}` = `\frac{du}{dy}`

Where `\frac{d\theta }{dt}` or `\frac{du}{dy}` is known as rate of shear strain.

∴ Rate of shear strain = `\frac{du}{dy}` or `\frac{d\theta }{dt}`

The term `\frac{du}{dy}` is also known as velocity gradient in y-direction.

Variation of shear stress with respect to distance (y) from surface:

The shear stress into the fluid decreases with an increase in height from the stationary surface.

At the stationary surface, the fluid has a higher velocity gradient (`\frac{du}{dy}`), thus the shear stress at this position is higher.

As the height (y) increases, the value of velocity gradient (`\frac{du}{dy}`) decreases. Thus the value of shear stress also decreases. Hence the value of shear stress is maximum at the stationary surface and minimum at the upper layer of fluid.

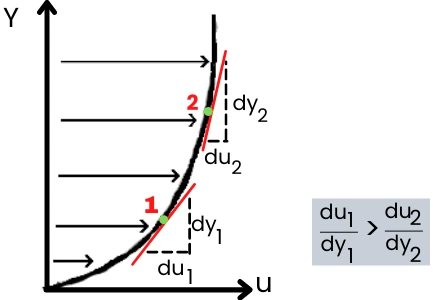
The above figure shows the variation of velocity (u) with respect to distance y. As shown in the figure, the velocity gradient at point 2 is less than the velocity gradient at point 1. Therefore the shear stress at point 2 will be less than the shear stress at point 1.

Significance of newton’s law of viscosity:

The significances of newtons law of viscosity are listed below:-

1. Newton’s law of viscosity states the relation between shear stress and the rate of shear strain in the moving fluids.
2. The newtons law of viscosity helps to find the shear stresses at different locations in the moving fluid.

Types of fluids as per the newton’s law of viscosity:

Based on newton’s law of viscosity, the fluids are classified as follows:-

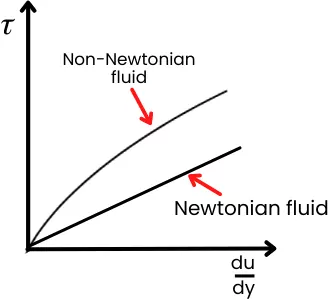
Newtonian fluid:- The fluids in which the shear stress is directly proportional to the rate of shear strain are known as Newtonian fluids.

Non-Newtonian fluids:- The fluids in which the shear stress is not directly proportional to the rate of shear strain are known as non-Newtonian fluids.

Newton’s law of viscosity problems:

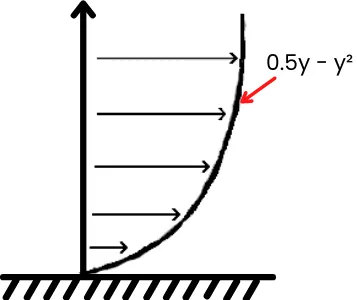
For the fluid flowing over the flat plate with a dynamic viscosity of 0.75 Ns/m², the velocity distribution in the fluid is given by u = 0.5y – y².
Determine the amount of shear stress at height y = 0.1m.

Given:
μ = 0.75 Ns/m²
u = 0.5y – y²

Solution:-

The rate of shear strain can be calculated as,

`\frac{du}{dy}` = `\frac{d}{dy}`(0.5y – y²)

`\mathbf{\frac{du}{dy}}` = 0.5 – 2y

At y = 0.1 m, the rate of shear strain is given by,

`(\frac{du}{dy})_{y = 0.1}` = 0.5 – 2(0.1)

`\mathbf{(\frac{du}{dy})_{y = 0.1}}` = 0.3

The shear stress at y = 0.1 m is given by,

`\tau` = `\mu(\frac{du}{dy})_{y=0.1}`

`\tau` = 0.75(0.3)

`\mathbf{\tau}` = 0.225 N/m²

Hence the shear stress at the height of 0.1 m is 0.225 N/m².

FAQ’s: