Potential energy (P.E.) is the energy associated with an object/body due to its position. This gravitational potential energy depends on various factors like the mass of an object, its height from the ground, and velocity.
But do you know how these factors actually affect the potential energy?
Potential energy rises with increasing an object’s mass and height (from the reference surface). Velocity at a particular instant never affects potential energy (P.E.) at that position, while the vertical component of the object’s velocity can cause a change in the P.E. of an object.
It is better to know more details about each of the factors.
Contents:
Mass effect on Potential energy:
The relation between the potential energy and mass is given by,
`P.E. = mgh`
`P.E. \propto m`
Thus, the potential energy (P.E.) is directly proportional to the object’s mass. P.E. increases with an increase in the mass of the object.
Thus for the same height from the ground, the heavier objects possess higher potential energy than lighter objects.
Let’s make it simpler with the help of the following example.
Take a tennis ball and a heavy bowling ball and release them from the same height from a table.
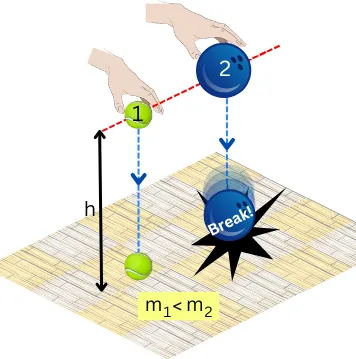
The lighter tennis ball will create a small impact on the floor but the bulky bowling ball can crash your flooring tiles.
Here the lighter (less mass) ball has less potential energy which creates less impact after converting into kinetic energy.
But due to the high mass, the bowling ball possesses higher potential energy which on converting into kinetic energy creates a high impact on the floor and crashes the tiles.
Height effect on Potential energy:
The relation between potential energy and the object’s height (h) from the reference position is given by,
`P.E. = mgh`
`P.E.\propto h`
Therefore, potential energy is directly proportional to the object’s height from the reference position. It means the potential energy of the object increases with an increase in the height of the object.
Example:
Release the heavy bowling ball from the height of the table. In another case release the same ball from the height of the tower.
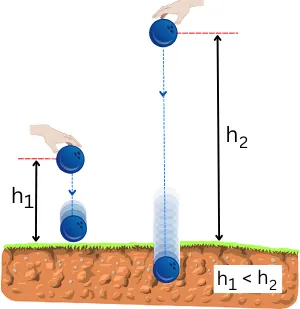
Here in this example, both balls have the same mass. But the ball falling from the height of the tower will hit the ground with greater force than the ball falling from the height of the table.
This happens because the ball at the tower’s height has higher potential energy than another ball. Thus this higher potential energy gets converted into higher kinetic energy and creates a high impact.
Velocity effect on Potential energy:
The potential energy depends on the position of the stationary or moving object. The object’s potential energy at a particular instant is never affected by its velocity at the same instant.
But the velocity of the vertically moving object changes the height of the object thus causing a change in the P.E. of the object.
For example, while throwing a ball in a vertically upward direction, the ball initially has less P.E. as it is closer to the ground. But it has a high K.E. due to its high velocity.
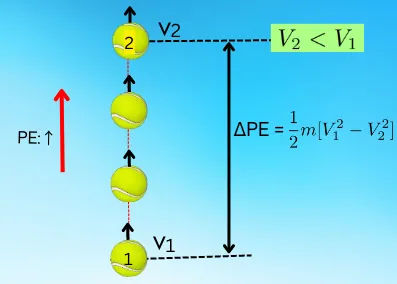
As the ball moves up, the velocity of the ball goes on decreasing due to the gravitational pull, and the P.E. of the ball goes on increasing.
For the ball shown in the above figure, the relation between the velocity and change in potential energy is given by,
∆PE = KE1 – KE2
`\Delta PE = \frac{1}{2}m.[V_{1}^{2} – V_{2}^{2}]`
When the velocity of the ball becomes zero, the PE of the ball reaches the maximum value.
Read also: