Contents:
What is Quasi static process?
The term quasistatic means almost seems to be static. The quasi static process is an ideal thermodynamic process that occurs slowly to maintain thermodynamic equilibrium throughout the process.
The quasi static process is also known as the quasi equilibrium process. This process takes infinite time for its completion.
The process generally seems to be in an equilibrium state therefore it is generally defined by the changes in parameters at two states, like change in pressure, change in volume, change in temperature, etc.
In the quasi static process, intensive properties change uniformly throughout the system.
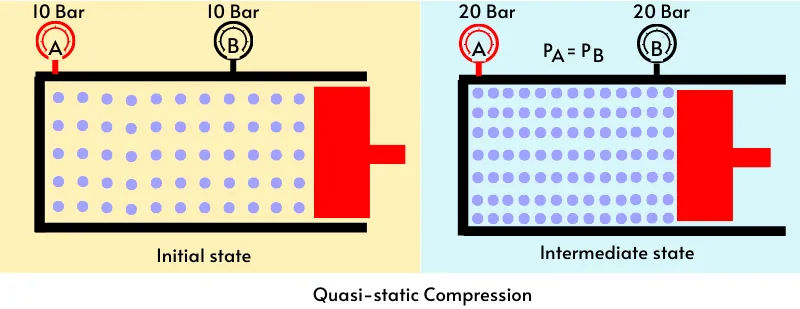
The below figure shows the quasi static compression of the gas in the piston and cylinder. At the start of compression, the pressure at gauge-A and gauge-B is same. As the compression is quasi static, the piston moves very slowly.
In this case, the inertia of the gas is not considerable, thus the molecules of the gas get enough time to adjust. Therefore at any intermediate state, the distribution of pressure throughout the cylinder becomes uniform and thus the gauge-A and gauge-B will record uniform pressure change throughout the compression.
It means that in a quasi static process, the properties of the system change uniformly. While in the non-quasi static process the variation of the properties in the system is non-uniform.
Due to the uniform distribution of the properties, the quasi static processes are represented by solid lines.
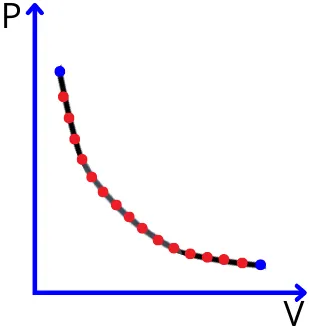
e.g.: The below figure-A shows the PV diagram for the quasi static process. As the property of the system varies uniformly, therefore we can plot the fixed values of pressure and volume on the P-V plot. Thus in the quasi static process, the processes are shown by the solid lines.
Characteristics of Quasi static process:
- The process seems to be in an equilibrium state.
- It is infinitely slower.
- The properties of the system change uniformly.
- Produces maximum work
Quasi static process example:
Here is an example that will help you to understand the quasi static processes in thermodynamics:-
Consider the certain quantity of gas is enclosed in a piston-cylinder assembly. The piston is loaded with total weight ‘W’ that consists of numerous infinitesimally smaller weights ‘dw’.
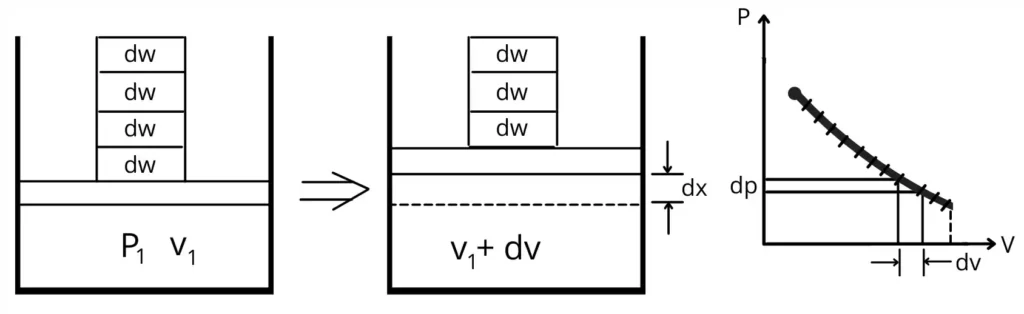
Initially, the gas enclosed in a cylinder is at pressure `P_{1}` and at volume `V_{1}`.
For this experiment, the procedure consists of reducing the pressure on the gas by removing one by one the smallest weights ‘dw’.
When we remove a single smallest weight ‘dw’ then the pressure on the gas gets decreased by the smallest quantity ‘dP’. To maintain the equilibrium, the piston moves upward by ‘dx’ to increase the volume by ‘dv’.
This change in volume is comparatively negligible therefore after this intermediate state the system will again attain thermodynamic equilibrium.
In the same manner, to remove the complete load ‘W’, the process will take much time and in this process, at each intermediate state, the system will attend the thermodynamic equilibrium.
Therefore this complete process is infinitesimally slower which seems to be in thermodynamic equilibrium at every intermediate state.
Non quasi static process:
The non-quasi static processes happen rapidly thus the intermediate states in these processes are not close to the equilibrium state.
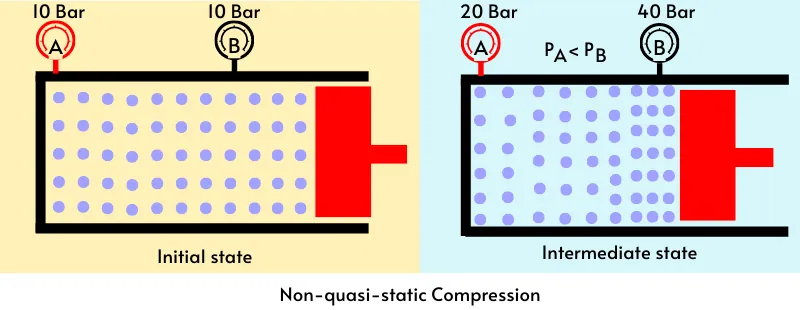
The above figure shows the non-quasi static compression of the gas in the piston-cylinder. At the start of compression, the distribution of the molecules is uniform, thus the pressure gauge-A and gauge-B record the same pressure.
During the non-quasi static compression, the piston moves rapidly. Because of the inertia, the gas molecules never get enough time to adjust. Thus the gauge near the piston (Gauge-B) indicates higher pressure than gauge-A. It means that the distribution of the pressure in the cylinder is non-uniform.
Hence in the non-quasi static process, the distribution of the intensive properties is non-uniform in the system. In such a process, it is difficult to plot the intermediate states. therefore on the graph, these processes are indicated by the dotted lines.
E.g.: for the process shown in the below graph, at a certain volume, the system shows different pressure values at different locations. Thus we cant plot fixed values of pressure. Thus the non-quasi static process is shown by the dotted line.
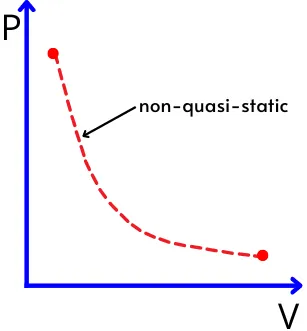
Due to the non-uniform distribution of the properties, the ideal gas equation is not applicable to this process.
Quasi static process work done:
Here is the equation of the work done for some of the quasi static processes:-
1] For constant pressure process:-
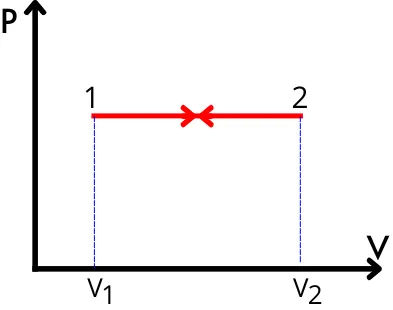
The work done in this process is equal to the area under the PV curve,
`\therefore W = \int_{V_{1}}^{V_{2}}P.dV`
`W = P\int_{V_{1}}^{V_{2}}.dV\cdots[\because\text{P=Constant}]`
`\mathbf{W = P[V_{2}-V_{1}]}`
2] For constant temperature process:-
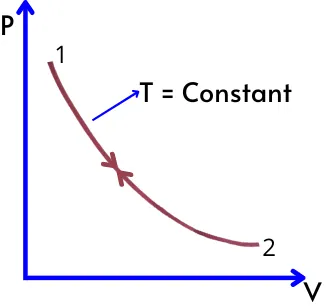
As the temperature is constant, thus as per the ideal gas equation,
`P.V = P_{1}.V_{1} = P_{2}.V_{2}` = mRT = Constant
`\therefore P = \frac{ P_{1}.V_{1}}{V}`
Now the work done is given by,
`W = \int_{V_{1}}^{V_{2}}P.dV`
`W = \int_{V_{1}}^{V_{2}}[\frac{ P_{1}.V_{1}}{V}].dV`
`W = P_{1}.V_{1}\int_{V_{1}}^{V_{2}}\frac{1}{V}.dV`
`W = P_{1}.V_{1}.[ln(V)]_{V_{1}}^{V_{2}}`
`W = P_{1}.V_{1}[ln(V_{2})-ln(V_{1})]`
`W = P_{1}.V_{1}.ln(\frac{V_{2}}{V_{1}})`
`\mathbf{W = mRT. ln(\frac{V_{2}}{V_{1}})} [\becauseP_{1}.V_{1}=mRT]`
3] For constant volume process:-
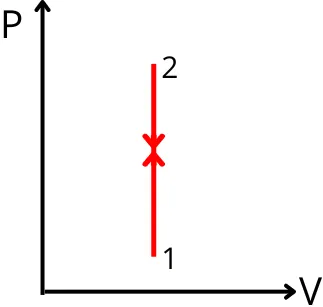
In this process, the volume of the system remains constant. Therefore, the change in volume of the system is zero (dV = 0).
Thus the work done is given by,
`W = \int P.dV`
`W = \int P.(0)`
W = 0
4] For polytropic process:-
In the polytropic process, the relation between the pressure and volume is given by,
`P.V^{n} = P_{1}.V_{1}^{n} = P_{2}.V_{2}^{n}` = Constant
`\therefore P = P_{1}.\frac{V_{1}^{n}}{V^{n}}`
Now the work done for the polytropic process is given by,
`W = \int_{V_{1}}^{V_{2}}P.dV`
`W = \int_{V_{1}}^{V_{2}}[P_{1}.\frac{V_{1}^{n}}{V^{n}}].dV`
`W = P_{1}.V_{1}^{n}\int_{V_{1}}^{V_{2}}\frac{1}{V^{n}}.dV`
`W = P_{1}.V_{1}^{n}\int_{V_{1}}^{V_{2}}V^{-n}.dV`
`W = P_{1}V_{1}^{n}[\frac{V^{-n+1}}{-n+1}]_{V_{1}}^{V_{2}}`
`W = \frac{P_{1}.V_{1}^{n}}{1-n}[V_{2}^{1-n}-V_{1}^{1-n}]`
`W = \frac{P_[1}.V_{1}^{n}V_{2}^{1-n}-P_{1}.V_{1}^{n}.V_{1}^{1-n}}{1-n}`
`W = \frac{\frac{P_{1}.V_{1}^{n}}{V_{2}^{n}}.V_{2}-P_{1}V_{1}}{1-n}`
As for the polytropic process,
`P_{1}.V_{1}^{n} = P_{2}.V_{2}^{n}`
`\therefore \frac{P_{1}.V_{1}^{n}}{V_{2}^{n}} = P_{2}`
Put this value in above equation of work done,
`W = \frac{P_{2}.V_{2}-P_{1}V_{1}}{1-n}`
`W = \frac{P_{1}.V_{1}-P_{2}.V_{2}}{n-1}`
`\mathbf{W = \frac{P_{1}.V_{1}}{n-1}[1-\frac{P_{2}.V_{2}}{P_{1}.V_{1}}]}`
FAQs:
-
Why is a quasi static process significant?
In a quasi static process, thermal equilibrium is maintained during all intermediate states and the variation of properties is uniform throughout the process.
-
Is the adiabatic process essentially quasi static?
The adiabatic process can be quasi static or non-quasi static.
-
Are quasi static processes irreversible?
The quasi static process can be irreversible or reversible.
-
What does “non-quasi static process” mean?
The process that occurs rapidly without maintaining thermodynamic equilibrium at the intermediate states is known as the non-quasi static process.
-
Is free expansion among quasi static processes?
No, free expansion is a quick process, thus it is not a quasi static process.
It should be word done at a constant temperature not constant pressure at the second of the last line.
Right, it was a typo.