Reverted gear train: Definition, Formula, Diagram, Examples

What is Reverted gear train?

Reverted gear train is one of the types of gear train in which the first input gear (gear on input shaft) and last output gear (gear on output shaft) are co-axial. In other words, the reverted gear train’s input and output gears have the same axis.

Because of this unique feature, the reverted gear train is suitable for applications where the input and output shafts are co-axial.

Another feature of this gear train is that the input gear and the output gear rotate in the same direction.

As shown in the below figure, the reverted gear train consists of the following components:- Input gear or first driver gear, output gear or last driven gear, and compound gears.

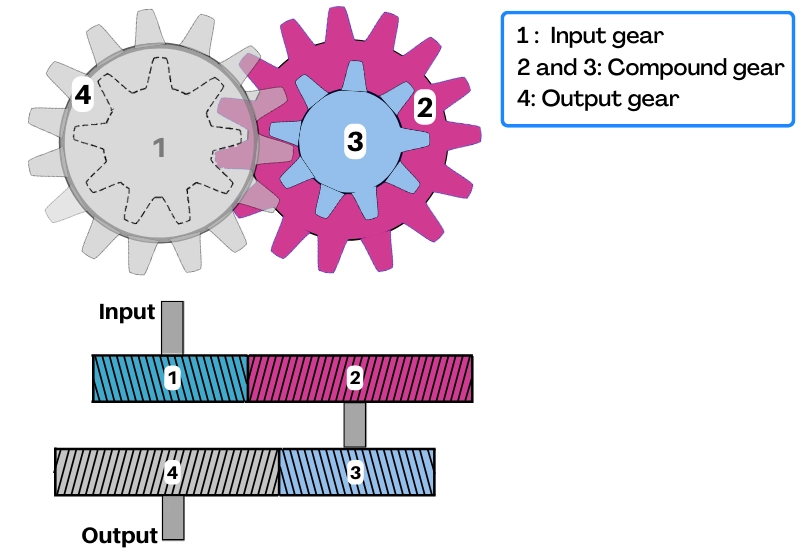
The gear-1 and gear 4 in the above figure are the input gear and the output gear respectively. Gear-2 and gear-3 are mounted on the same shaft to form a compound gear, thus gear-2 and gear-3 rotate together at the same speed.

Explanation:

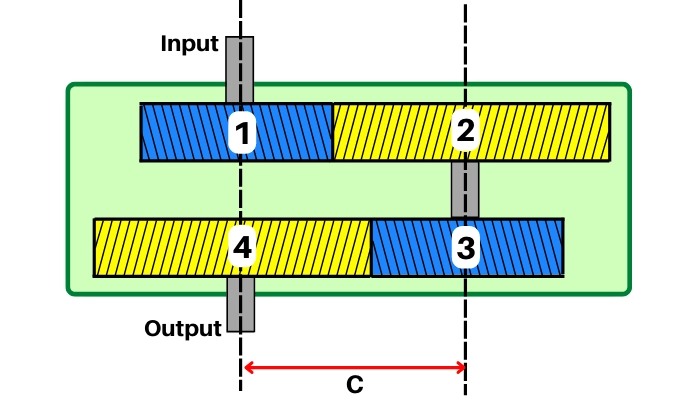
For the 2-stage reverted gear train shown in the above figure, as the input and output shafts are co-axial, thus the center distance between gear-1 and gear-2 is equal to the center distance between gears-3 and gear-4.

∴ `C_{12}` = `C_{34}` = C

As, `C_{12}` = `r_{1}` + `r_{2}` and `C_{34}` = `r_{3}` + `r_{4}`, thus the above equation will become,

∴ `r_{1}` + `r_{2}` = `r_{3}` + `r_{4}`

Where,
`r_{1}, r_{2}, r_{3}, r_{4}` = Pitch circle radius of respective gear

The above equation gives the relation between the pitch circle radius of the gears of the reverted gear train.

As r = `\frac{d}{2}`, thus the above equation becomes,

`\frac{d_{1}}{2}`+`\frac{d_{2}}{2}`=`\frac{d_{3}}{2}`+`\frac{d_{4}}{2}`

`d_{1}` + `d_{2}` = `d_{3}` + `d_{4}`

The above equation gives the relation between the pitch circle diameter of the gears of the 2-stage reverted gear train.

As d = m x t, hence the above equation becomes,

`m_{12}t_{1}` + `m_{12}t_{2}` = `m_{34}t_{3}` + `m_{34}t_{4}`

`m_{12}(t_{1} + t_{2})` = `m_{34}(t_{3}+t_{4})`

Where,
`m_{12}` = Module of the gear-1 and gear-2
`m_{34}` = Module of gear-3 and gear-4
`t_{1}, t_{2}, t_{3}, t_{4}` = Number of teeth on the each gear of gear train

For the gear train with same module (`m_{12}` = `m_{34}`), the above equation becomes,

`t_{1}` + `t_{2}` = `t_{3}` + `t_{4}`

The above equation gives the relation between the number of teeth on gears of a 2-stage reverted gear train with the same module.

Reverted gear train formula:

Following are some of the formulae used for the analysis of the 2-stage reverted gear train:-

1] Speed ratio:-

The speed ratio (gear ratio) equation of the reverted gear train is given by,

i = `\frac{\text{Product of number of teeth of all follower}}{\text{Product of number of teeth of all drivers}}`

Where,
Followers:- Gears (except idler) driven by another gear
Driver:- Gears (except idler) that drives another gear

2] Relation between pitch circle radii:-

The relation between the pitch circle radius of all gear is given by,

`r_{1}` + `r_{2}` = `r_{3}` + `r_{4}`

Where `r_{1}, r_{2}, r_{3}, r_{4}` = Pitch circle radius of respective gear

3] Relation between number of teeth:-

The relation between number of teeth of all gears of reverted gear train is given by,

`m_{12}(t_{1}+t_{2})` = `m_{34}(t_{3}+t_{4})`

Where,
`t_{1}, t_{2}, t_{3}, t_{4}` = Number of teeth on the each gear of gear train
`m_{12}` = Module of gear-1 and gear-2
`m_{34}` = Module of gear-3 and gear-4

For the reverted gear train with same module,

`t_{1}` + `t_{2}` = `t_{3}` + `t_{4}`

Advantages:

The reverted gear train has the following advantages:-

1. It can fit between co-axial shafts.
2. The reverted gear train can obtain a higher gear ratio within less space.

Applications:

The reverted gear train helps to obtain a higher gear ratio within limited space, thus it is used in various applications as follows:-

1] Back gear mechanism is lathe:-
The lathe machine uses a reverted gear train in a back gear mechanism to achieve more speed reduction.

2] Back gear mechanism in vertical drill machine:-
In vertical drill machines, a reverted gear train is used as a back gear mechanism to obtain two different speed ratios.

3] Automobile transmision:-
The reverted gear train is used in car transmissions to provide multiple gear ratios in a small space using co-axial input and output shafts.

4] Clock:-
As all hands of the clock are co-axial, therefore it uses a reverted gear train to obtain the correct speed of the hands.

5] Industrial gearbox:-
The various equipment used in industries uses gearboxes based on the reverted gear train. In such a gearbox, the input and output shafts are co-axial.

Difference between reverted and compound gear train:

Sr. No.	Reverted gear train	Compound gear train
1	The input and output shafts are co-axial.	In this type of gear train, the output and the input shafts are not co-axial.
2	The direction of rotation for the input and output gear is the same.	The direction of rotation of the input and output shaft may or may not be the same.
3	It is used in applications where input and output shafts connected to the gearbox are co-axial.	It is used where a sufficient center distance is present between the input and output shaft.
4	Example: Automobile transmission.	Example: Lathe, Valve timing gears in automobiles, etc.

Reverted gear train problems and solutions:

1] The input shaft of the given reverted gear train rotates at 1440 RPM. a] Find the number of teeth of 3rd gear if, `t_{1}` = 20, `t_{2}` = 50, `t_{4}` = 55 b] Find gear ratio c] Speed of output shaft [Assume module is same for all gears]

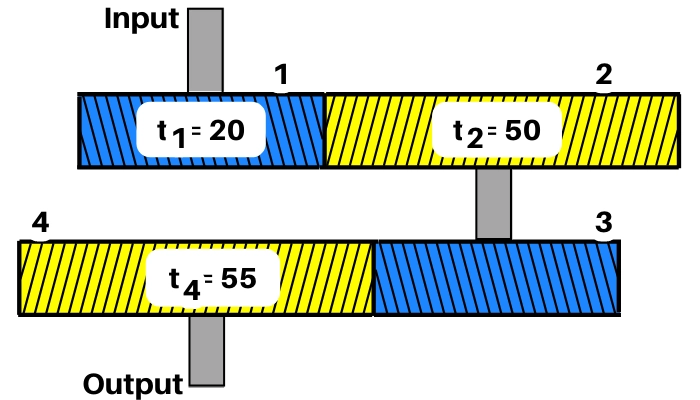
Solution:-

a] Number of teeth of `\mathbf{3^{\text{rd}}}` gear:-

If the all gears have same module then for the reverted gear train the relation between the number of teeth is given by,

`t_{1}` + `t_{2}` = `t_{3}` + `t_{4}`

20 + 50 = `t_{3}` + 55

`t_{3}` = 15 teeth

∴ The `\mathbf{3^{\text{rd}}}` gear has 15 teeth.

b] Gear ratio:-

The gear ratio of the above gear train is given by,

i = `\frac{\text{Product of the no. of teeth of follower/driven gears}}{\text{Product of the no. of teeth of driver}}`

In the above figure, gear-1 and gear-3 are driver gears and gear-2 and gear-4 are followers.

∴ i = `\frac{t_{2} \times t_{4}}{t_{1} \times t_{3}}` = `\frac{50\times 55}{20\times 15}`

i = 9.166

c] Speed of output shaft:-

The equation for the speed ratio is given by,

i = `\frac{N_{1}}{N_{4}}`

9.166 = `\frac{1440}{N_{4}}`

`N_{4}` = 157.102 RPM

Thus the speed of the output shaft is 157.102 RPM.

---

2] For the below reverted gear train, the gear ratios for each pair of gear are, `i_{12}` = 2, `i_{34}` = 2.95. The center distance between the input shaft and the compound shaft is 0.15 m. If the module for the whole gear train is 2 mm then find the number of teeth on each gear of the gear train

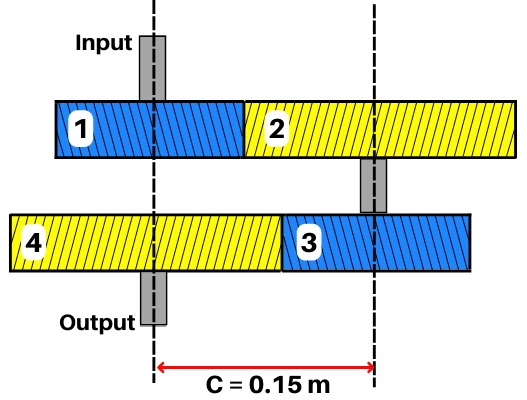
Given:-
`i_{12}` = 2
`i_{34}` = 2.95
C = 0.15 m = 150 mm
m = 2 mm

Solution:-

a] Number of teeth on gear 1 and gear 2:-
The center distance between gears 1 and 2 is given by,

`\frac{d_{1}}{2}` + `\frac{d_{2}}{2}` = C

`\frac{m.t_{1}}{2}` + `\frac{m.t_{2}}{2}` = C ——–[∵ d = m x t]

`\frac{2.t_{1}}{2}` + `\frac{2.t_{2}}{2}` = 150

`\mathbf{t_{1} + t_{2}}` = 150 —–Equation [1]

The gear ratio of the `1^{\text{st}}` pair of gear is given by,

`i_{12}` = `\frac{t_{2}}{t_{1}}`

2 = `\frac{t_{2}}{t_{1}}`

∴ `t_{2}` = `2t_{1}`

Put this value of `t_{2}` in above equation [1],

`t_{1}` + `2t_{1}` = 150

`t_{1}` = 50 teeth

`t_{1}` = 50 teeth

The number of teeth on `2^{\text{nd}}` gear is given by,

`t_{2}` = `2t_{1}` = 2 x 50

`t_{2}` = 100 teeth

b] Number of teeth on gears 3 and 4:-

The center distance between gears 3 and 4 is given by,

`\frac{d_{3}}{2}`+`\frac{d_{4}}{2}` = C

`\frac{mt_{3}}{2}`+`\frac{mt_{4}}{2}` = C ——–[∵d = m x t]

`\frac{2t_{3}}{2}`+`\frac{2t_{4}}{2}` = 150

`t_{3}` + `t_{4}` = 150 – Equation [2]

The gear ratio for the `2^{\text{nd}}` pair of gear is given by,

`i_{34}` = `\frac{t_{4}}{t_{3}}`

2.95 = `\frac{t_{4}}{t_{3}}`

`t_{4}` = 2.95 `t_{3}`

Put this value of `t_{4}`in above equation [2]

`t_{3}` + 2.95`t_{3}` = 150

`t_{3}` = 37.974

`t_{3}` ≈ 38 Teeth

The number of teeth on `4^{\text{th}}` gear is given by,

`t_{4}` = 2.95`t_{3}`

`t_{4}` = 2.95 x 37.974

`t_{4}` = 112.02

`t_{4}` ≈ 112 Teeth

Thus the number of teeth for a given reverted gear train are,

`t_{1}` = 50, `t_{2}` = 110
`t_{3}` = 38, `t_{4}` = 112

FAQs:

The reverted gear train is used in various applications because of its unique feature. We hope that this article has given you enough information to understand the concept of a reverted gear train. If you like the above post then check our other posts related to the different categories of mechanical or automobile engineering.

Related articles:

• Simple gear train – Explained
• All about Compound gear train