What is Reynolds transport theorem?
The Reynolds transport theorem says that the rate of change of an extensive property of a system with respect to time is equal to the sum of the rate of change of property per unit time for a control volume and rate of efflux of the property.
The Reynolds transport theorem is the major theorem which helps to derive different conservation laws like, conservation of mass, Conservation of momentum, Conservation of linear momentum, etc.
Contents:
Reynolds transport theorem equation:
The following is the general form of the Reynolds transport theorem.
`[\frac{dB}{dt}]_{system}=\frac{d}{dt}\int \int \int_{CV} b\rho .dforall+\int \int_{CS} b\rho (\vec{V}.\hat{n}).dA`
Where,
B = Extensive property
b = Specific property (B/m)
ρ = Density
`\hat{n}` = Unit direction vector.
Reynolds transport theorem derivation:
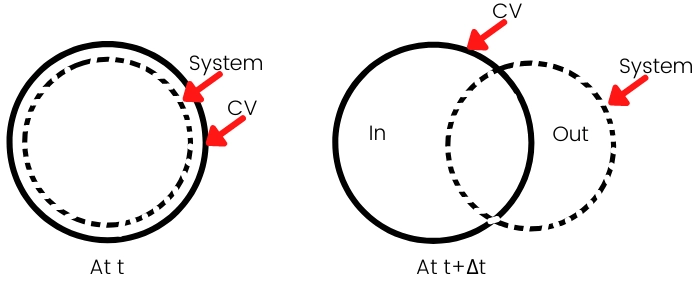
The above figure shows the boundaries of the system and control volume. The control volume is the portion used for the analysis and this figure has a fixed control volume and the system is the set of mass or the bunch of molecules. In this case, the volume of control volume remains constant here.
E.g. for the water held in the bucket, the bucket is considered as control volume while the water is considered as a system.
Now consider all the extensive properties are denoted by B and the intensive properties are denoted by symbol b.
`\text{Where}, b=\frac{B}{m}`
Therefore at time t, the relation between properties of system and CV is given by,
`B_{[\text{System}]t}=B_{[CV]t}` ————[1]
Now after some time interval at t + Δt, the properties of the system is given by, [See the above figure]
`B_{[\text{System}][t+\Delta t]}=B_{[CV][t+\Delta t]}+B_{[Out][t+\Delta t]}-B_{[\text{in}][t+\Delta t]}` ———-[2]
The rate of change in property of system after the time interval of Δt is given by,
`\frac{\Delta B_{\text{system}}}{\Delta t}=\frac{B_{[\text{system}][t+\Delta t]}-B_{[\text{system}][t]}}{\Delta t}`
Put the values from equation [1] and [2],
`\frac{\Delta B_{System}}{\Delta t}=\frac{{B_{[CV][t+\Delta t]}+B_{[Out][t+\Delta t]}-B_{[\text{in}][t+\Delta t]}}-{B_{[CV][t]}}}{\Delta t}`
`\frac{\Delta B_{System}}{\Delta t}=\frac{B_{[CV][t+\Delta t]}-B_{[CV][t]}}{\Delta t}+\frac{B_{[Out][t+\Delta t]}}{\Delta t}-\frac{B_{[\text{in}][t+\Delta t]}}{\Delta t}`
Take limit on both sides with Δt → 0,
`\lim_{\Delta t\rightarrow 0}\frac{\Delta B_{System}}{\Delta t}=\lim_{\Delta t\rightarrow 0}\frac{B_{[CV][t+\Delta t]}-B_{[CV][t]}}{\Delta t}+\lim_{\Delta t\rightarrow 0}\frac{B_{[Out][t+\Delta t]}}{\Delta t}-\lim_{\Delta t\rightarrow 0}\frac{B_{[\text{in}][t+\Delta t]}}{\Delta t}\cdots[3]`
Where,
i] `\lim_{\Delta t\rightarrow 0}\frac{\Delta B_{System}}{\Delta t}=[\frac{dB}{dt}]_{\text{System}}`
ii] `\lim_{\Delta t\rightarrow 0}\frac{B_{[CV][t+\Delta t]}-B_{[CV][t]}}{\Delta t}=\lim_{\Delta t\rightarrow 0} \frac{\Delta B_{CV}}{\Delta t}=[\frac{\partial B}{\partial t}]_{CV}`
iii] `\lim_{\Delta t\rightarrow 0}\frac{B_{[Out][t+\Delta t]}}{\Delta t}=\lim_{\Delta t\rightarrow 0}\frac{b_{Out}m_{Out}}{\Delta t}\cdots` (As b = B/m)
`=\lim_{\Delta t\rightarrow 0}\frac{b_{Out}.\rho _{Out}\forall _{Out}}{\Delta t}\cdots` (As `\rho = \frac{m}{forall}`)
`=\lim_{\Delta t\rightarrow 0}\frac{b_{Out}.\rho _{Out}A_{Out}x_{Out}}{\Delta t}\cdots` (As `forall`=A.x)
`=\lim_{\Delta t\rightarrow 0}\frac{b_{Out}.\rho _{Out}A_{Out}V_{Out}\Delta t}{\Delta t}\cdots` (As `V_{Out}=\frac{x}{\Delta t}`)
`=\lim_{\Delta t\rightarrow 0}{b_{Out}.\rho _{Out}A_{Out}V_{Out}}`
`=\{b_{Out}.\rho _{Out}A_{Out}V_{Out}}`
`\lim_{\Delta t\rightarrow 0}\frac{B_{[Out][t+\Delta t]}}{\Delta t}={b_{Out}.\rho _{Out}A_{Out}V_{Out}}`
iv] Similarly, `\lim_{\Delta t\rightarrow 0}\frac{B_{[In][t+\Delta t]}}{\Delta t}={b_{\text{in}}.\rho _{\text{in}}A_{\text{in}}V_{\text{in}}}`
Therefore putting all the values from i, ii, iii, iv in equation [3]
`[\frac{dB}{dt}]_{System}=[\frac{\partial B}{\partial t}]_{CV}+{b_{Out}.\rho _{Out}A_{Out}V_{Out}}-{b_{In}.\rho _{In}A_{In}V_{In}}`
`[\frac{dB}{dt}]_{System}=[\frac{\partial B}{\partial t}]_{CV}+[\dot{B_{O}}-\dot{B_{i}}]`
Where `[\dot{B_{O}}-\dot{B_{i}}]` is the reflux
Where
`\dot{B_{O}}={b_{Out}.\rho _{Out}A_{Out}V_{Out}}`
`\dot{B_{i}}={b_{\text{in}}.\rho _{\text{in}}A_{\text{in}}V_{\text{in}}}`
General form of Reynolds transport theorem:
The general form of the reynolds transport theorem is given by,
`[\frac{dB}{dt}]_{System}=\frac{\partial }{\partial t}\int \int \int_{CV} b\rho d forall + \int \int_{CS}b\rho (\vec{V}.\hat{n}).dA`
Reynolds transport theorem for different properties:
For mass:
For mass as the property put B = m and `b=\frac{B}{m}=\frac{m}{m}=1`
Now by putting values in Reynold transport theorem,
`\frac{dm}{dt}=\frac{\partial }{\partial t}\int \int \int_{CV} \rho d\forall + \int \int_{CS}\rho (\vec{V}.\hat{n}).dA`
But by the statement of conservation of mass,
`\frac{dm}{dt}=0`
∴ The equation will becomes,
`0=\frac{\partial }{\partial t}\int \int \int_{CV} \rho d\forall + \int \int_{CS}\rho (\vec{V}.\hat{n}).dA`
∴ The equation of reynold transport theorem for mass is,
`\frac{\partial }{\partial t}\int \int \int_{CV} \rho d forall + \int \int_{CS}\rho (\vec{V}.\hat{n}).dA` = 0
For momentum:
For the linear momentum,
B = m`\vec{V}` and `b=\frac{B}{m}=\frac{m\vec{V}}{m}=\vec{V}`
Now put these values in the Reynolds transport theorem,
`\frac{d}{dt}[m\vec{V}]_{System}=\frac{\partial }{\partial t}\int \int \int_{CV} \rho \vec{V} d forall + \int \int_{CS}\rho \vec{V} (\vec{V}.\hat{n}).dA`
As per the Newtons second law,
`\frac{d}{dt}[m.\vec{V}]=m.a=F`
Therefore the equation becomes,
`\frac{\partial }{\partial t}\int \int \int_{CV} \rho \vec{V} d forall + \int \int_{CS}\rho \vec{V} (\vec{V}.\hat{n}).dA=F`
For angular momentum:
For the angular momentum
Put B = `m(\vec{r}\times \vec{V})`
`b=\frac{B}{m}=\frac{m(\vec{r}\times \vec{V})}{m}`=`(\vec{r}\times \vec{V})`
Now put these values in Reynolds transport theorem,
`\frac{d}{dt}[m(\vec{r}\times \vec{V})]=\frac{\partial }{\partial t}\int \int \int_{CV} \rho (\vec{r}\times \vec{V}) d forall + \int \int_{CS}\rho (\vec{r}\times \vec{V}) (\vec{V}.\hat{n}).dA`
Where, `\frac{d}{dt}[m(\vec{r}\times \vec{V})]` = T – – – – – – -[T = torque]
∴ The equation will become,
`\frac{\partial }{\partial t}\int \int \int_{CV} \rho (\vec{r}\times \vec{V}) d forall + \int \int_{CS}\rho (\vec{r}\times \vec{V}) (\vec{V}.\hat{n}).dA=T`