The rotational equilibrium is the type of mechanical equilibrium considered in the case of rotational motion. In this article, we are discussing the rotational equilibrium in great detail.
Contents:
What is Rotational equilibrium?
Rotational equilibrium states that the net torque acting on the object is zero as well as it has zero angular acceleration.
Thus for rotational equlibrium,
`\mathbf{\sum \vec{T}}` = 0
Where `\sum \vec{T}` shows the vector sum of the torque acting on the object.
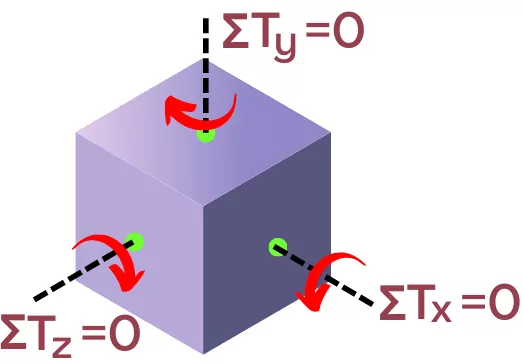
In scalar form, the conditions for rotational equilibrium are given by,
Σ`\mathbf{T_{x}}` = 0
Σ`\mathbf{T_{y}}` = 0
Σ`\mathbf{T_{z}}` = 0
As the object under rotational equilibrium has zero net torque, therefore according to Newton’s 2nd law of rotation (T = 𝙸α), such object has zero angular acceleration (α = 0).
Hence the object under rotational equilibrium may be stationary or rotates with a constant angular velocity (ω = Constant).
Rotational equilibrium equations:
The condition of rotational equilibrium in vector form is given by,
`\mathbf{\sum \vec{T}}` = 0
In scalar form, the rotational equilibrium conditions are as follows,
Σ`\mathbf{T_{x}}` = 0
Σ`\mathbf{T_{y}}` = 0
Σ`\mathbf{T_{z}}` = 0
Rotational equilibrium explained:
Here are two distinct examples that will make it easier to learn rotational equilibrium:-
1] Fan rotating at a constant speed:-
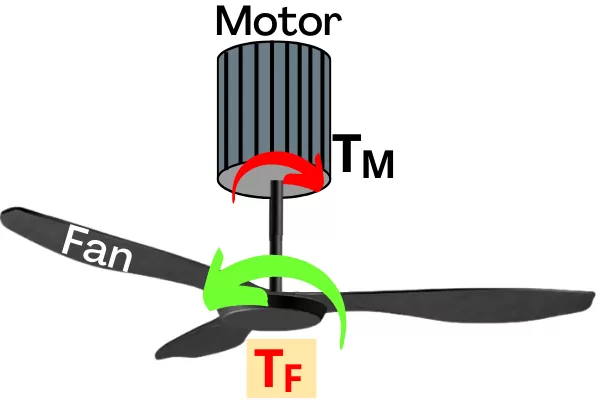
The above figure shows the fan rotating at a constant speed. In this case, the motor develops a torque of `T_{M}` while the aerodynamic forces acting onto the fan blades develop equal and opposite torque `T_{F}`.
Thus the net torque acting on the fan is given by,
ΣT = `T_{M}` – `T_{F}`
As the magnitudes of `T_{M}` and `T_{F}` are equal,
∴ ΣT = 0
As the net torque acting on the fan is zero, therefore the fan rotating at constant speed is said to be in rotational equilibrium. Due to the zero net torque, the fan rotates with zero angular acceleration.
2] Cantilever beam:-
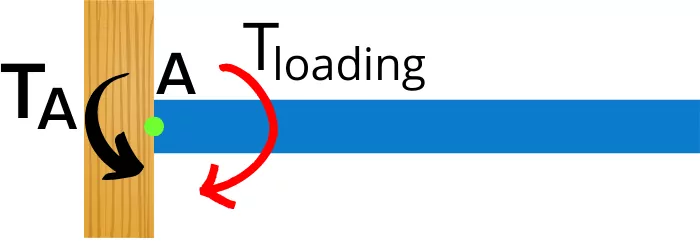
The above figure shows the cantilever beam, fixed at support A. The load on the cantilever beam develops a torque `T_{\text{loading}}` at the point ‘A’ and in contrast, the support develops equal and opposite torque `T_{A}` at point ‘A’.
Thus the net torque acting at support is given by,
ΣT = `T_{A}` – `T_{\text{loading}}` [Consider ↺ +ve]
As, the magnitudes of `T_{A}` and `T_{\text{loading}}` are equal,
∴ ΣT = 0
Thus due to the zero net torque, the beam is said to be in rotational equilibrium.
Therefore, The object under rotational equilibrium may be stationary like a cantilever beam or it may rotate at a constant angular speed like a fan.
Rotational equilibrium solved examples:
1] The weightless beam ABC is hinged to the support at end A and supported by the rope BD. If the crate of mass 35 kg is kept at end 'C', then find the tension in rope BD.
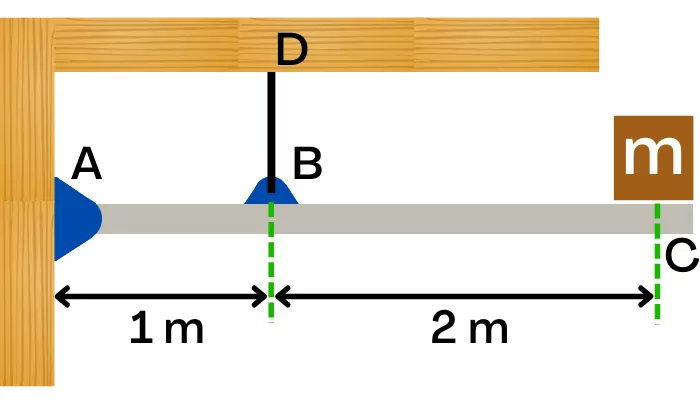
Given:-
m = 35 kg
`L_{AB}` = 1 m
`L_{BC}` = 2 m
`L_{AC}` = 3 m
Solution:-
Step 1] Free body diagram:-
The free body diagram of the beam ABC is as follows:-
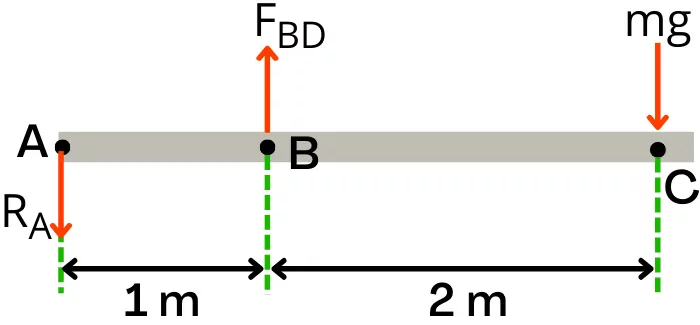
Step 2] Apply rotational equilibrium conditions:-
Applying rotational equilibrium condition at hinge `A`,
Σ`T_{A}` = 0 [Consider ↻ +ve]
– (`F_{BD}` ✕ `L_{AB}`) + (mg ✕ `L_{AC}`) + (`R_{A}` ✕ 0) = 0
– (`F_{BD}` ✕ 1) + ([35 ✕ 9.81] ✕ 3) = 0
| `\mathbf{F_{BD}}` = 1030.05 N |
This is the magnitude of the tension in rope BD.
2] Find distance x in below figure so that the seesaw will be in rotational equlibrium.
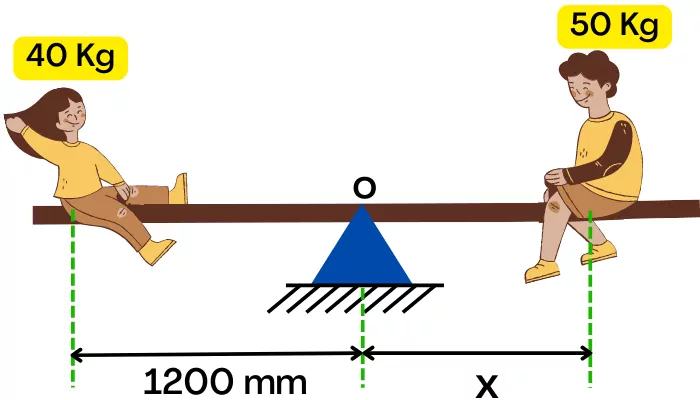
Solution:-
Step 1] Free body diagram:-
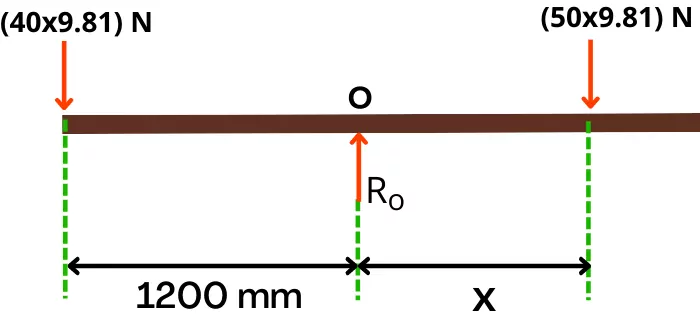
Step 2] Apply rotational equilibrium conditions:-
Applying rotational equilibrium condition at hinge ‘O’,
`\sum T_{O}` = 0 (Consider ↻ +ve)
{(50 ✕ 9.81) ✕ x} – {(40 ✕ 9.81)✕ 1200} = 0
| x = 960 mm |
FAQs:
-
When a body is in rotational equilibrium?
A body is in rotational equilibrium when the net torque acting on the object is zero.
-
How is rotational equilibrium attained?
To attain the rotational equilibrium, the net torque acting on the object should be equal to zero.
-
What is an example of rotational equilibrium?
The examples of a rotational equilibrium are as follows,
1] Fan rotating at a constant speed
2] Balanced seesaw. -
Can an object be in translational equilibrium but not in rotational equilibrium?
The object rotating with non-zero angular acceleration experiences non-zero net torque. Such objects that rotate with angular acceleration and have zero linear acceleration are in translational equilibrium but not in rotational equilibrium.
Example:- While starting the ceiling fan rotates with positive angular acceleration to attain its maximum speed but it has zero linear acceleration. During this period, the fan is in translational equilibrium but not in rotational equilibrium -
Whether the object rotating at a constant angular speed is in rotational equilibrium?
The object rotating at constant angular speed has zero angular acceleration and zero net torque which means that the object is under rotational equilibrium.
You might be interested in these as well: