Contents:
What is schottky defect?
Schottky defect is the type of point defect that occurs due to the missing of an equal number of cations and anions from the lattice position with keeping their positions vacant.
This Schottky defect generally occurs in ionic crystals like NaCl, KCl, AgBr, etc.
The Schottky defect is always observed as pairs of vacant positions that are created due to the missing of an equal number of cations and anions.
In this case, both the cation and anion have comparable sizes.
As these atoms leave the structure permanently, this results in a decrease in the density of the crystal.
How does schottky defects arise?
By supplying the heat to the lattice, the atoms gain the enthalpy required for the defect formation. Due to this, the temperature of the crystal increases, and the excitation of the atoms about their lattice position increases.
Due to this excitation, n number of cations, as well as n number of anions, escapes from their lattice position which results in the formation of vacancies at this lattice position, which is known as Schottky defect.
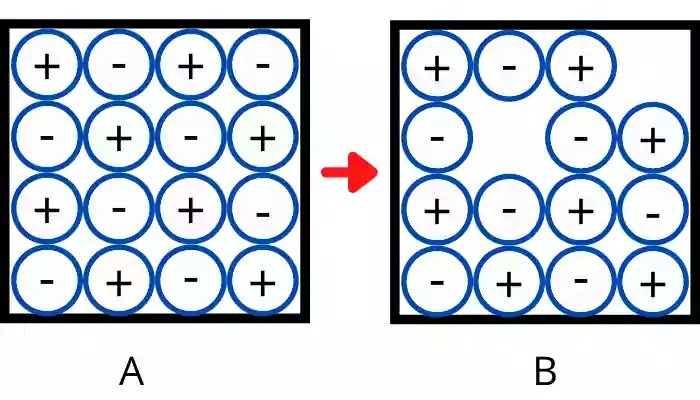
Example:- Here figure A shows the 2D structure of the NaCl crystal before the formation of the Schottky defect. After gaining the enthalpy of the defect formation, some of the positive ions (`Na^{+}`) and the equal number of negative ions (`Cl^{-}`) leave their position in a lattice structure and result in the formation of Schottky defect. Figure B shows the crystal structure after the formation of the Schottky defect.
Schottky defect density:
Because of the Schottky defect in the crystal lattice, its density decreases since due to the Schottky defect, the ‘n’ number of cations and ‘n’ number of anions escapes from their position in the crystal lattice, keeping the space void.
Therefore the total mass of the crystal decreases but the volume remains constant and therefore it results in lowering the density of the crystal.
Schottky defect equation:
The number fo schottky defects in unit volume of crystal is given by,
`n_{s}` = `N\times e^{-\frac{\Delta H_{S}}{2KT}}`
Where,
N = Number of cations/anions per unit volume
T = Temperature in K
`\Delta H_{s}` = Enthalpy for creating one schottky defect
`n_{s}` = Number of schottky defects occurs per unit volume
K = Boltzman constant
Schottky defect example:
In case of the NaCl crystal structure, at temperature of 2700 K if the mole fraction for the schottky defect is X. Calculate the – ln(x), if `\Delta H_{s}` = 2 eV, K = `\mathbf{1.38 \times 10^{-23}}` J/K.
Given:
T = 2700 K
Enthalpy for single defect formation, `\Delta H_{s}` = 2 eV = 2 x `(1.608 \times 10^{-19})` J = `3.216 \times 10^{-19}` J
Boltzmann constant, K= `1.38 \times 10^{-23}` J/K
SOLUTION:-
In NaCl crystal,
n = Number of schottky defect
`N_{A}` = Avagadro’s number
N = Number of cations/anions
Therefore,
Number of moles of ions = `\frac{N}{N_{A}}`
Number of moles of the Schottky defect = `\frac{n}{N_{A}}`
Mole fraction of the Schottky defect (X) is given by,
Mole fraction, (X) = `\frac{\text{Moles of defect}}{\text{Moles of defect + Moles of ions}}`
Mole fraction, (X) = `\frac{\frac{n}{N_{A}}}{(\frac{n}{N_{A}}+\frac{N}{N_{A}})}`
Mole fraction, (X) = `frac{n}{n+N}`
X = `\frac{\frac{n}{N}}{\frac{n}{N}+1}` ——– Eq[1]
But the number of schottky defects is given by,
n = `N \times e^{-\frac{\Delta H_{S}}{2KT}}`
Put this value of n in equation [1]
X =`\frac{e^{-\frac{\Delta H}{2KT}}}{e^{-\frac{\Delta H}{2KT}}+1}`
Where, `\frac{\Delta H}{2KT}` = `\frac{[3.216\times 10^{-19}]}{2\times [1.38\times 10^{-23}]\times 2700}`
`\frac{\Delta H}{2KT}`= 4.315
Putting the value of `\frac{\Delta H}{2KT}` in equation of mole fraction X,
Hence, mole fraction X becomes,
X = `\frac{e^{-4.315}}{e^{-4.315}+1}`
X = 0.01319
Taking negative log of both sides,
– ln(X) = – ln(0.01319)
– ln(X) = 4.32
FAQ’s
-
What is Schottky defect give an example?
The Schottky defect is the lattice defect that arises due to the escape of an equal number of cations and anions from the lattice positions. Eg. NaCl, AgBr, etc.
-
What are Schottky and Frenkel defects?
The Schottky defect is the lattice defect that arises due to the escape of an equal number of cations of anions from the lattice positions.
The Frenkel defect arises due to the escaping of the cation from its own position and takes an interstitial position in lattice. -
What is the difference between Frenkel and Schottky defect?
The main difference between Frenkel and Schottky defects is that in Frenkel defect the cation moves from its original position to the interstitial position and in the case of Schottky defect, the cation, and anion escape permanently from the lattice structure.
-
What is the effect of presence of Schottky defects on the density of a crystal?
The presence of the Schottky defect decreases the density of a crystal.
-
When Schottky defect is observed in crystals?
The Schottky defect is observed when an equal number of anions and cations are missing from the lattice structure.
-
What happens in Schottky defect?
The Schottky defect causes the missing of an equal number of anions and the cations from the lattice structure.