Contents:
What is Spring constant?
Spring constant can be defined as restoring force generated into the spring for a unit length of deflection. It is also known as the amount of force required for the unit length of extension or compression in spring.
The spring constant states the amount of resistance offered to the deformation in the spring. The spring constant is also known as spring stiffness or spring rate and it is denoted by the symbol ‘K’.
The spring constant of the coil spring depends on the following factors:-
a) Modulus of rigidity (G): The spring constant of the coil spring increases with the increase in the modulus of rigidity of the spring material.
b) Wire diameter (d): The spring constant increases with the increase in the spring wire diameter.
c) Coil diameter (D): The spring constant of the spring decreases with the increase in spring coil diameter.
d) Number of coils (n): The spring constant decreases with the increase in the number of coils of the spring.
Spring constant explained:
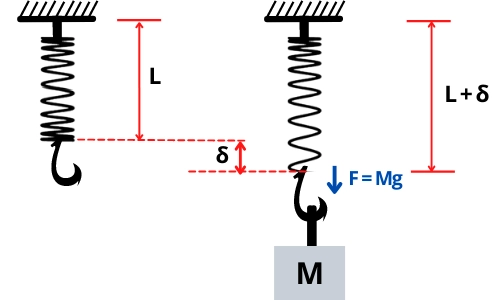
As shown in the above figure: A, the mass M is suspended at the end of the spring.
After the application of load, the spring gets stretched by the distance 𝛿.
Similarly, If we increase the amount of load, the spring will extend more and more & if we lower the amount of load then the spring will retract in the same manner.
The relation between this force F and change in length 𝛿 can be given by,
F = K𝛿
Here, K is the spring constant.
Spring constant in hooke’s law:
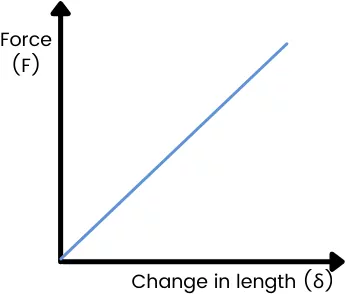
Hooke’s law for the spring says that the amount of force required for extension or compression of the spring is linearly proportional to the change in length of the spring.
F ∝ 𝛿
F = K𝛿
Where,
F = Force for extension/compression in spring
𝛿 = Change in length of spring
K = Spring constant
The restoring force (Fs) developed in spring works opposite to the force applied.
∴ `F_{s}` = – `F`
∴ `F_{s}` = – K𝛿
The spring constant is given by,
K = `-\frac{F_{S}}{\delta}`
Or
K = `\frac{F}{\delta}`
Spring constant formula:
The formula to calculate spring constant (K) is as follows.
K = -`\frac{F_{s}}{\delta}` Or K = `\frac{F}{\delta}`
Where,
`F_{s}` = Restoring force in spring (N)
𝛿 = Deformation in spring (m)
F = Force applied to spring
The spring constant equation with mass is given by,
F = `\frac{Mg}{\delta}`
Where,
M = Load (Kg)
g = Acceleration due to gravity (N/m²)
Spring constant units:
In SI system:-
In an SI system, the unit of the force is Newton (N) and the unit of distance is meter (m), Therefore,
Spring constant (K) = `\frac{F}{\delta}` = `\frac{N}{m}`
Hence the SI unit of the spring constant is N/m.
In FPS system:-
In FPS system, the unit of force is lb and the unit of distance is ft, therefore,
Spring constant (K) = `\frac{F}{\delta}` = `\frac{lb}{ft}`
Hence FPS unit of spring constant is lb/ft.
Spring constant dimensional formula:
The spring constant (K) is given by,
K = `\frac{F}{\delta}`
The dimensional formula of force are,
F = [`MLT^{-2}`]
And the dimensional formula of deflection are,
𝛿 = [M⁰LT⁰]
Therefore the dimensional formula of spring constant (K) is given by,
K = `\frac{F}{\delta}` = `\frac{[MLT^{-2}]}{[M^{0}LT^{0}]}` = [`MT^{-2}`]
Therefore the dimensional formula for spring constant K is [`MT^{-2}`].
How to calculate spring constant from graph?
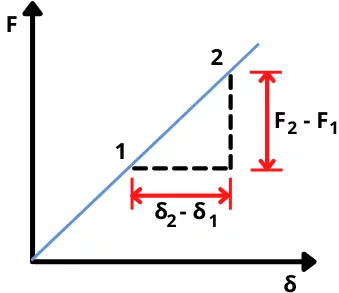
The above figure shows the graph of force (F) vs deflection (δ). The spring constant from this graph can be calculated by taking the slope of this graph.
Therefore from the above graph, the spring constant can be calculated as,
K = Slope of F-δ curve = `\frac{F_{2}-F_{1}}{\delta_{2}-\delta_{1}}`
Can spring constant be Negative?
The value of the spring constant never becomes negative.
The slope of the Force-deflection curve always becomes positive, therefore the value of the spring constant also remains positive.
Spring constant examples:
Find the amount of deflection in the spring (K = 20 N/mm) for hanging 20 Kg of the mass. (g = 9.81 m/s²)
Given:
K = 20 N/mm
M = 20 Kg
g = 9.81 m/s²
Solution:
The deflection in the spring can be find using following equation,
K = `\frac{Mg}{\delta}`
20 = `\frac{20 \times 9.81}{\delta}`
`\delta` = 9.81 mm.
Therefore the spring gets deflected by 9.81 mm.
FAQs:
-
How does the spring constant depends on the loaded weights?
The value of the spring constant never depends on the loaded weight, it remains constant for the different loaded weights.
-
Is there any effect of length of spring on spring constant?
The spring constant never depends on the length of the spring. The factors on which the spring constant depends are the Modulus of rigidity (G), Coil diameter (D), Wire diameter (d), Number of coils (n).
-
Do all springs have the same spring constant?
No, the spring constant is not the same for all the springs as it depends on the material of the spring and some of the spring dimensions.
-
What does a high spring constant mean?
The high spring constant means that the spring requires a higher force for making the smaller deflection in the spring.
-
Does spring constant change with compression?
No, the spring constant remains same for the different magnitudes of the compression forces.
-
How do you find the spring constant from the load extension graph?
The slope of the load-extension graph gives the spring constant (K) of the spring.