Contents:
What is critical pressure ratio?
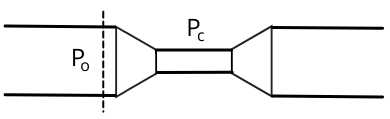
Critical pressure ratio is the ratio of pressure at which the system gives maximum mass flow rate and it cannot be increased further by adjusting the system pressure.
The critical pressure ratio of any fluid depends on the polytropic index (n) of that fluid.
This maximum mass flow rate condition is reached when the match number at minimum cross-section becomes equal to 1.
The critical pressure calculated at downstream is also known as choking pressure. It means that if the pressure at downstream decreased below the critical pressure then choking will occur.
Critical pressure ratio equation:
By the definition, the critical pressure ratio is given by,
Critical pressure ratio = `\frac{P_{c}}{P_{o}}`
Where `P_{c}` = Pressure at the minimum cross-section
`P_{o}` = Inlet pressure
Critical pressure ratio of nozzle formula:
The critical pressure ratio formula for the nozzle is given by,
Critical pressure ratio = `\frac{P_{c}}{P_{o}}=(\frac{2}{n+1})^{\frac{n}{n-1}}`
Where n = polytropic index of the fluid
Significance of critical pressure ratio:
The significance of the critical pressure ratio is given below
- The critical pressure ratio helps to attain maximum mass flow rate through the nozzle.
- It also helps us to avoid choking of nozzle.
Critical pressure ratio for air:
For air, the value of the polytropic index is given by,
n = 1.41
By using the formula of critical pressure ratio,
`\frac{P_{c}}{P_{o}}=(\frac{2}{n+1})^{\frac{n}{n-1}}`
`=(\frac{2}{1.41+1})^{\frac{1.41}{1.41-1}}`
= 0.526
Hence for air, the critical pressure ratio is 0.526
Critical pressure ratio for steam:
For saturated steam, the value of the polytropic index is given by,
n = 1.135
By using the formula of critical pressure ratio,
`\frac{P_{c}}{P_{o}}=(\frac{2}{n+1})^{\frac{n}{n-1}}`
`=(\frac{2}{1.135+1})^{\frac{1.135}{1.135-1}}`
= 0.577
For air, the critical pressure ratio is 0.577