The key point that differentiates the Neutral axis vs Centroid is that the neutral axis indicates the imaginary axis at which the beam under bending load experiences zero stress whereas the centroid is the imaginary point that indicates the geometric mean position of the plane lamina.
Neutral axis:
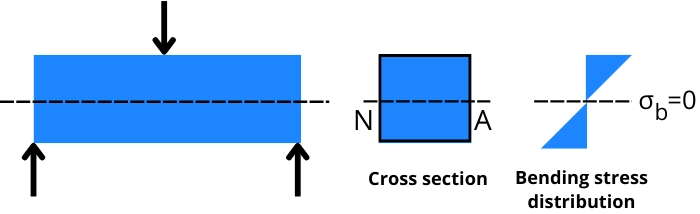
The neutral axis is the line passing through the cross-section of the object (subjected to a bending load) at which the fibers of the object experience zero stress and zero strain.
For the beam subjected to the bending load (see above figure), the portion above the neutral axis experiences compressive stress and the portion below the neutral axis experiences tensile stress.
At the neutral axis, the stress changes its nature from compressive to tensile. Thus the fibers at the neutral axis never experience bending stress. (`\sigma_{b}` = 0)
The position of the neutral axis varies depending on whether the deformation is elastic or plastic, and the neutral axis is thus classified as an elastic neutral axis or plastic neutral axis.
The elastic neutral axis of any object with a homogeneous cross-section passes through its centroid. The plastic neutral axis divides the area of the cross-section into two halves.
Centroid:
Centroid is the point at which the total area of the plane surface is assumed to be concentrated.
It is also known as the geometric center of the plane lamina.
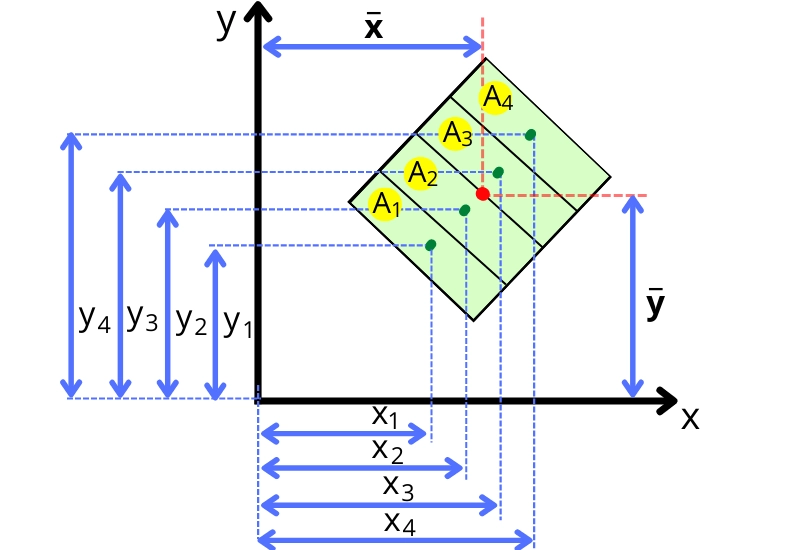
For the object shown in the above figure, the position of the centroid is given by,
From y-axis,
`\bar{x}` = `\frac{\sum_{i=1}^{n}A_{i}x_{i}}{\sum_{i=1}^{n}A_{i}}`
From x-axis,
`\bar{y}` = `\frac{\sum_{i=1}^{n}A_{i}y_{i}}{\sum_{i=1}^{n}A_{i}}`
In the form of integration, the position of the centroid is given as follows,
`\bar{x}` = `\frac{\int x.dA}{\int dA}` , `\bar{y}` = `\frac{\int y.dA}{\int dA}`
The centroid has much importance in the structural analysis of the components subjected to the different types of loadings.
Neutral axis vs Centroid – Difference:
| Sr. No. | Neutral axis | Centroid |
|---|---|---|
| 1 | It is the line passing through the cross-section of the beam subjected to the bending load at which the fibers of the beam experience zero stress and strain. | The centroid is the geometric center of the plane lamina. It is also known as the center of gravity of a plane lamina. |
| 2 | It is an imaginary line passing through the cross-section. | It is an imaginary point on the cross-section of an object. |
| 3 | It indicates the fibers of the beam with no stress and strain. | It indicates the mean position of all points in the plane figure. |
| 4 | It is necessary to find a neutral axis during an analysis of an object subjected to bending loading. | It is necessary to find the centroid during the torsional, bending analysis of the object. |
| 5 | The neutral axis passes through the cross-section of the shape. | The centroid may be positioned outside of the shape. |
| 6 | The position of the neutral axis depends on the direction of the applied force or bending movement. | The position of the centroid never depends on the direction of the applied force. |