We know that the term energy indicates the ability of the object for performing some sort of work. Similarly, the ability of the object to perform rotational work indicates its rotational kinetic energy.
In this article, we are going to cover all the information about rotational kinetic energy to help you understand the subject matter thoroughly.
Contents:
What is Rotational kinetic energy?
Rotational kinetic energy is the energy possessed by the object due to its rotational motion OR in other words, we can say that it is the kinetic energy of a rotating object.
Here are a few examples that will clarify what rotational kinetic energy (RKE) is:-
- Energy possed by the ceiling fan because of its rotary motion.
- Energy possessed by the earth due to its rotational motion.
- Energy possessed by rotating toy-top.
- Energy of rotating flywheel.
RKE is directly proportional to the moment of inertia (I) and the square of angular velocity (`\omega`) of the object.
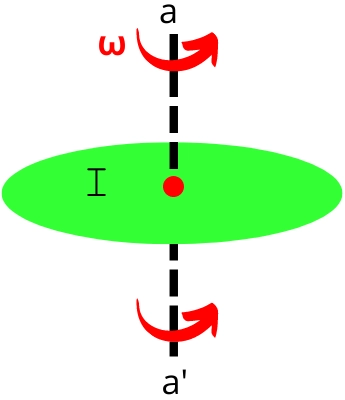
The above figure shows the object rotating at angular velocity `\omega` about axis a-a’. The rotational KE possessed by the above object is given by,
`KE_{R}=\frac{1}{2}I\omega^{2}`
The term rotational kinetic energy (RKE) is analogous to the translational kinetic energy used in a translational motion.
The translational kinetic energy depends on the mass and translational velocity of the object whereas the Rotational kinetic energy depends on the moment of inertia (analogous to mass in translational motion) and angular velocity (`\omega`) (analogous to the translational velocity).
Rotational kinetic energy equation:
The kinetic energy of the object rotating at angular velocity (`\omega`) is given by,
`KE_{R}=\frac{1}{2}I\omega^{2}`
Where,
`I` = Moment of inertia (MOI) about the axis of rotation
`\omega` = Angular velocity
While in the terms of angular momentum, it is given by,
`KE_{R}=\frac{L^{2}}{2I}`
Where,
L = Angular momentum = `I\omega`
Rotational kinetic energy units:
Since it is a type of energy, its units are the same as those for energy, which are as follows:-
- SI system:- Joule (J)
- MKS system:- Kg.m²/s²
- FPS unit:- lbm.ft²/s²
The dimensional formula for the rotational kinetic energy is [M¹L²T⁻²].
How to calculate rotational kinetic energy?
For a rotating object, it can be found by use of the following steps:-
- Find the moment of inertia (MOI) about the axis of rotation of an object (I).
- Find the angular velocity of the object about the axis of rotation.
- Find rotational kinetic energy by use of the formula shown below,
`KE_{R}=\frac{1}{2}I\omega^{2}`
Rotational kinetic energy derivation:
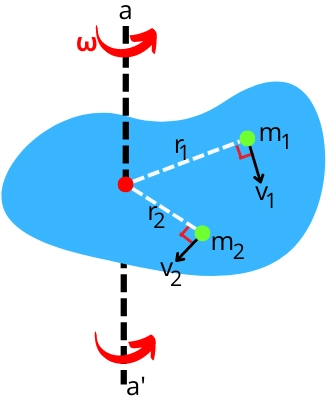
Consider an rotating object consist of number of point mass (`m_{1}, m_{2}, \cdots m_{n}`) located at different radii (`r_{1}, r_{2}, \cdots r_{n}`) from the axis of rotation (a – a’). As the object is rotating, each point mass in the object is also rotating with its respective tangential velocity.
The total kinetic energy possessed by an object due to each of the individual mass is given by,
`KE=KE_{m1}+KE_{m2}\cdots +KE_{mn}`
`KE=\frac{1}{2}m_{1}v_{1}^{2}+\frac{1}{2}m_{2}v_{2}^{2} \cdots +\frac{1}{2}m_{n}v_{n}^{2}`
`KE=\frac{1}{2}m_{1}(r_{1}\omega)^{2} + \frac{1}{2}m_{2}(r_{2}\omega)^{2} \cdots +\frac{1}{2}m_{n}(r_{n}\omega)^{2} [\because v = r \omega]`
`KE=\frac{1}{2}[m_{1}r_{1}^{2}+m_{2}r_{2}^{2} \cdots +m_{n}r_{n}^{2}]\omega^{2}`
`KE=\frac{1}{2} [\sum_{i=1}^{n}m_{n}r_{n}^{2}]\omega^{2}`
As `\sum m_{n}r_{n}^{2}` is the total moment of inertia of the object (I) about the axis of rotation, thus the equation becomes,
`KE=\frac{1}{2}I\omega^{2}`
Where,
`KE=KE_{R}` = Rotational kinetic energy (RKE)
I = Moment of inertia (MOI) about the axis of rotation
`\omega` = Angular velocity
RKE of some shapes:
Here we have listed the rotational kinetic energy of some of the standard shapes:-
1] Sphere:-
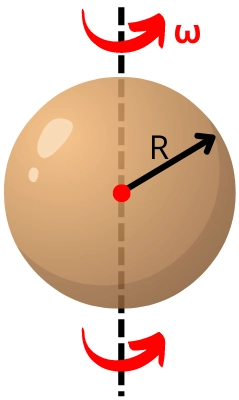
The moment of inertia of a solid sphere about an axis passing through its center is given by,
`I=\frac{2}{5}mR^{2}`
Now the rotational kinetic energy for the sphere becomes,
`KE_{R}=\frac{1}{2}I\omega^{2}`
`=\frac{1}{2}(\frac{2}{5}mR^{2})\omega^{2}`
`\mathbf{KE_{R}=\frac{mR^{2}\omega^{2}}{5}}`
2] Disc:-
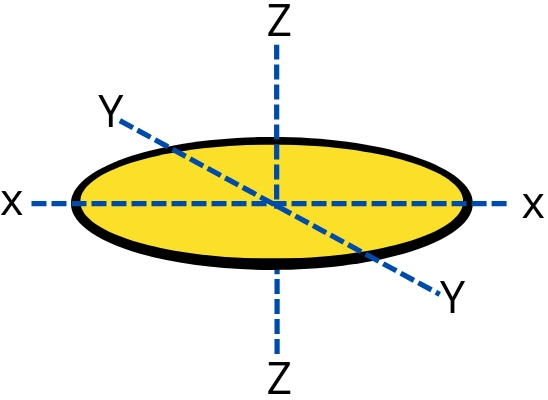
The moment of inertia of a solid disc about an axis lying in the plane of the disc and passing through its centroid is given by,
`I_{x}=I_{y}=\frac{1}{4}mR^{2}`
The moment of inertia of a disc about an axis perpendicular to the plane of the disc is given by,
`I_{z}=\frac{1}{2}mR^{2}`
If the disc is rotating about the x-axis or y-axis then the rotational kinetic energy (RKE) of the disc is given by,
`KE_{x}=KE_{y}=\frac{1}{2}I_{x}\omega^{2}`
`=\frac{1}{2}(\frac{1}{4}mR^{2})\omega^{2}`
`\mathbf{KE_{x}=\frac{mR^{2}\omega^{2}}{8}}`
If the disc is rotating about the z-axis then the RKE is given by,
`KE_{z}=\frac{1}{2}I_{z}\omega^{2}`
`=\frac{1}{2}(\frac{1}{2}mR^{2})\omega^{2}`
`\mathbf{KE_{z}=\frac{mR^{2}\omega^{2}}{4}}`
Solved examples:
1] Find the rotational kinetic energy (RKE) of the earth. Assume earth has a moment of inertia about a polar axis of 8.038 x 10³⁷ kg.m² and angular velocity of 7.29 x 10⁻⁵ rad/s.
Given:-
I = 8.038 x 10³⁷ kg.m²
`\omega` = 7.29 x 10⁻⁵ rad/s
Solution:-
`KE_{R}=\frac{1}{2}I\omega^{2}`
`KE_{R}=\frac{1}{2}(8.038 \times 10^{37})\times(7.29 \times 10^{-5})^{2}`
`\mathbf{KE_{R}=2.135 \times 10^{29}}` Joule
2] A torque of 0.8 N.m cause the cylinder to accelerate from rest. The cylinder has a mass of 2 Kg and a radius of 200 mm. what is the Rotational kinetic energy of the cylinder at t = 2 s.
Given:-
T = 0.8 N.m
m = 2 Kg
R = 200 mm = 0.2 m
t = 2 Seconds
Solution:-
The moment of inertia of the cylinder about its longitudinal axis is given by,
`I=\frac{1}{2}mR^{2}`
`I=\frac{1}{2} \times 2 \times 0.2^{2}`
`I=0.04` Kg.m²
The angular acceleration (`\alpha`) in the cylinder is given by,
`T=I \alpha`
`0.8=0.04 \times \alpha`
`\alpha=20` rad/s²
The angular velocity (`\omega_{2}`) of the cylinder after 2 seconds is given by,
`\alpha=\frac{\omega_{2}-\omega_{1}}{t}`
`20=\frac{\omega_{2}-0}{2} [\because \omega_{1}=0 \text{(initially at rest)}]`
`\omega_{2}=40` rad/s
The RKE of the cylinder after 2 seconds is given by,
`KE_{R}=\frac{1}{2}I\omega_{2}^{2} = \frac{1}{2}0.04 \times 40^{2}`
`\mathbf{KE_{R}=32}` J
FAQs:
-
What causes a rise in rotational kinetic energy?
The rotational kinetic energy increases with,
increase in angular velocity
increase in mass
farther distribution of mass from the axis of rotation. -
What four elements influence the kinetic energy of rotation?
The following factors influence the rotational kinetic energy,
1] Angular velocity
2] Distribution of mass abound the axis of rotation
3] Mass of the object
4] Position of the axis of rotation. -
Is there rotational kinetic energy on Earth?
Yes, the earth also has rotational kinetic energy because of its rotational motion.
-
Is it possible for rotational kinetic energy to be negative?
Because the moment of inertia is a positive term and the square of the angular velocity is also a positive term, the rotational kinetic energy never turns negative.
-
Is it possible for an object to have both rotational and linear kinetic energy?
Yes, the objects in rolling motion (e.g. wheel) possess both translational and rotational kinetic energy.
Related post: