We all know that in order to throw something at great speed, we must first perform some work on it. In such instances, the work-energy theorem, also known as the work-energy principle, can provide the relationship between the work done on the item and its speed.
This article explains the work-energy theorem in detail and includes some practice numerical examples for a clear understanding of the topic.
Contents:
What is the Work-energy theorem?
The work-energy theorem states that the net work done by the forces on the object is equal to the change in kinetic energy of the object. It states the relationship between the net work done on an object and the change in the kinetic energy of an object.
This theorem obeys the law of energy conservation.
Let me explain it with the example of golf.
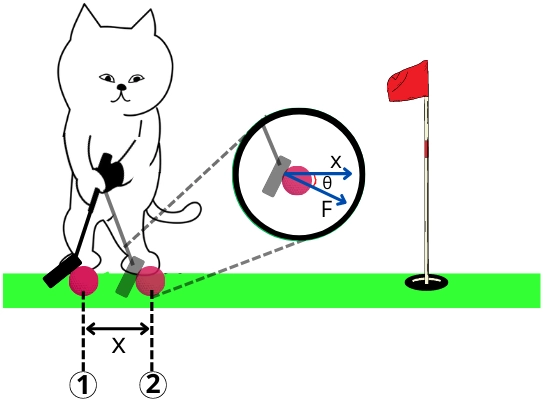
The golfer in the above figure tries to push the ball by applying force (F) on the ball for the distance of ‘x’.
The vertical component of the force (Fsinθ) is not responsible for doing work on the ball. To push the golf ball, the horizontal component of the force (Fcosθ) in the direction of the displacement does the work which is given by,
`W = F.cosθ.x`
During the interaction period between the golf stick and the ball, the work done by the golf stick gets transformed to raise the velocity of the golf ball. It means that the net work done onto the ball is responsible for the change in kinetic energy of the ball.
`\frac{1}{2}mv_{2}^{2}-\frac{1}{2}mv_{1}^{2}= W`
`KE_{2}-KE_{1} = W`
It means that the change in kinetic energy of the ball (ΔKE) is equal to the `W_{\text{net}}` on the ball.
Work-energy theorem derivation:
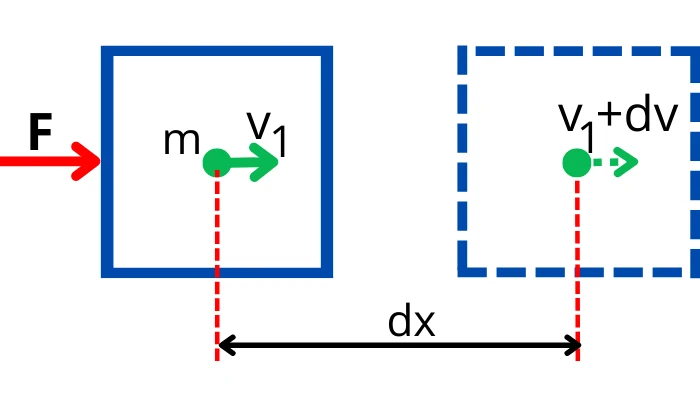
Consider an object of mass ‘m’ moving at velocity `V_{1}` is subjected to a variable force ‘F’.
During the smaller time interval of ‘dt’, the object shows a smaller displacement dx. Therefore the small work done by force on the object is given by,
`dw = F.dx`
`dw = m.a.dx \cdots \cdots [ \because F = ma]`
`dw = m.\frac{dv}{dt}.dx \cdots \cdots [ \because a = \frac{dv}{dt}]`
`dw = m\frac{dx}{dt}.dv`
`dw = m.v.dv \cdots[ \because \frac{dx}{dt} = v]`
Integrate the equation to find the work done to change the velocity of the object from `V_{1}` to `V_{2}`.
`W = \int dw = \int_{V_{1}}^{V_{2}}m.v.dv`
`W = m \int_{V_{1}}^{V_{2}}v.dv`
`W = m[\frac{v^{2}}{2}]_{V_{1}}^{V_{2}}`
`W = m[\frac{V_{2}^{2}}{2}-\frac{V_{1}^{2}}{2}]`
`W = \frac{mV_{2}^{2}}{2} – \frac{mV_{1}^{2}}{2}`
`W = KE_{2}-KE_{1}`
`W = \DeltaKE`
Thus it proves that the work done by the force onto the object is equal to the change in kinetic energy of the object.
Alternate method:-
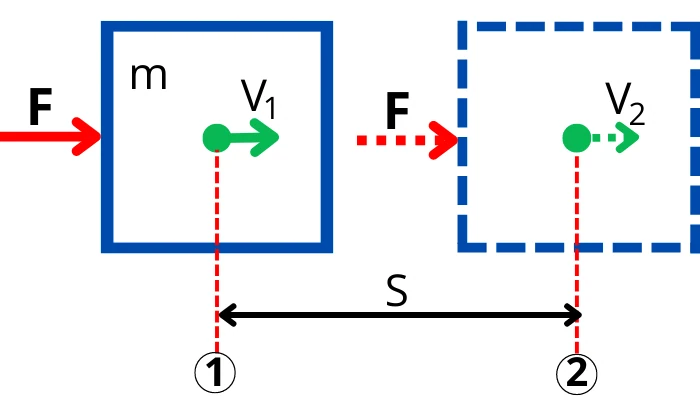
As shown in the above figure, the net force F acting on the object causes to change its velocity. Thus the work done by force on an object to move it from position 1 to 2 is given by,
W = F.S
According to one of the newtons equations of linear motion,
`V_{2}^{2} =V_{1}^{2} + 2aS`
∴ `S = \frac{V_{2}^{2}-V_{1}^{2}}{2a}`
Put this value of S in the equation of work.
`W = F \times \frac{V_{2}^{2}-V_{1}^{2}}{2a}`
`W = m.a \times \frac{V_{2}^{2}-V_{1}^{2}}{2a} \cdots [ \because F = ma]`
`W = \frac{mV_{2}^{2}}{2}-\frac{mV_{1}^{2}}{2}`
`W = KE_{2}-KE_{1}`
`W = \Delta KE`
Therefore it proves the work energy theorem.
Work-energy theorem solved examples:
1] A bullet of a mass of 10 grams hits the wooden object at the velocity of 790 m/s and it penetrates the object up to 100 mm to stop. By assuming the force applied by the bullet is constant, find the average force applied by the bullet on the object.
Given:-
m = 10 g = 0.01 Kg
`V_{1}` = 790 m/s
`V_{2}` = 0 m/s
S = 100 mm = 0.1 m
Solution:-
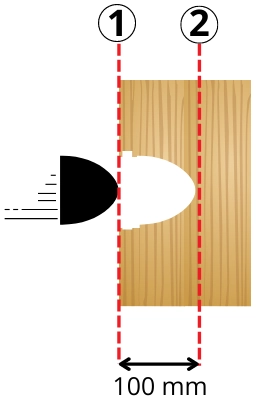
By the work-energy theorem,
Work done by bullet = Change in kinetic energy of the bullet
`-(F \times S) = KE_{2}-KE_{1}`
Here negative sign indicates work is done by the bullet.
`- (F \times S) = \frac{mV_{2}^{2}}{2}-\frac{mV_{1}^{2}}{2}`
` – (F \times 0.1) = \frac{0.01 \times 0^{2}}{2}-\frac{0.01 \times 790^{2}}{2}`
F = 31205 N
∴ F = 31.205 KN
This is the magnitude of average force applied by a bullet on the wooden object.
2] The children are pulling two blocks A & B from the rest that has a mass of 30 kg each. After pulling up to the distance of 3 m, the block gains a velocity of 1.5 m/s. If the coefficient of friction between block and ground is 0.3 then find the average uniform force applied by the children.
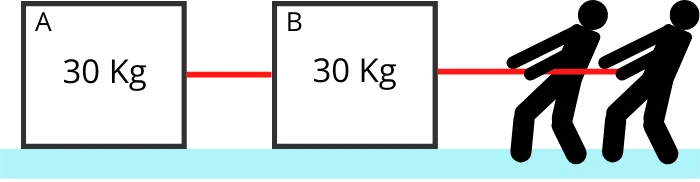
Given:-
`m_{A}` = `m_{B}` = 30 Kg
`\text{Weight}, w_{A}=w_{B}=mg =30 \times 9.81=294.3 N`
`V_{1}` = 0 m/s
`V_{2}` = 1.5 m/s
µ = 0.3
S = 3 m
Solution:-
Free body diagram:-
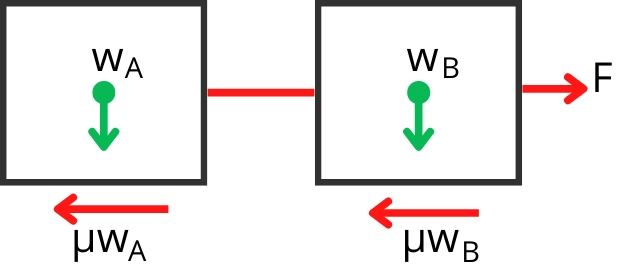
The net force acting on blocks is given by,
`F_{\text{net}} = F-\muw_{B}-\muw_{A}`
`F_{\text{net}} = F-0.3(294.3)- 0.3(294.3)`
`F_{\text{net}} = (F-176.58)N`
The total change in kinetic energy of the system is given by,
`\DeltaKE = KE_{2}-KE_{1}`
`= \frac{1}{2}(m_{A}+m_{B})V_{2}^{2}-\frac{1}{2}(m_{A}+m_{B})V_{1}^{2}`
`= \frac{1}{2}(30+30)1.5^{2}-\frac{1}{2}(30+30)0^{2}`
`\DeltaKE` = 67.5 N.m
Now as per the work-energy theorem,
`W_{\text{net}} = \DeltaKE`
`F_{\text{net}} \times S = \DeltaKE`
(F – 176.58) x 3 = 67.5
F = 199.08 N
It is the magnitude of the average uniform force applied by children.
Application:
The work-energy theorem has application in analyzing the motion of a rigid object that is subjected to several motion-affecting forces.
FAQs:
-
Why is the work-energy theorem important?
The work-energy theorem gives the relationship between the forces applied to the object and the motion of the object.
-
What is the formula of the work-energy theorem?
The work-energy theorem formula is as follows,
Change in kinetic energy = Work -
When can you use the work-energy theorem?
The work-energy theorem can be used to find the unknown forces that are responsible for the motion or it can be used for the analysis of the motion of the object.
-
How to calculate speed using the work-energy theorem?
From the work-energy theorem, the initial or final speed of the object can be calculated as follows,
Net work = [(1/2)mV₂²] – [(1/2)mV₁²]
Where,
V₂ = Final speed
V₁ = Initial speed -
How to find distance using the work-energy theorem?
From the work-energy theorem, the distance responsible for the work done can be calculated as follows,
F.d.cosθ = Change in kinetic energy
Where,
F = Net force
d = Distance
θ = Angle between the force and displacement vector -
What does the work-kinetic energy theory say about the speed of a satellite?
According to the work-energy theorem, since the net work done on the satellite is zero, the change in kinetic energy of the satellite is also zero. That is, the satellite moves at a constant speed.
We included all of the work-energy theorem’s necessary information. I hope you grasped the topic completely. You can get it in PDF format by clicking the button below.
Related post: