What is the conjugate beam method?
The conjugate beam is the method used to determine the slope and deflection of the complex beam.
In this method, the imaginary conjugate beam is constructed from the real beam. The shear forces and bending moments of the conjugate beam are equal to the slope and deflection of the real beam.
The Beam with different flexural rigidity can also be solved by the conjugate beam method.
Following are the terms used in the conjugate beam method:
1] Real beam: the beam with the actual loads and supports is known as a real beam.
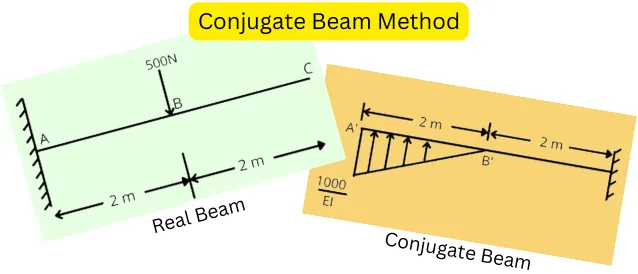
2] Conjugate Beam: It is an imaginary beam that has the same length as a real beam, but in this case, the loading is equal to the ratio of bending moment (M) of the real beam to flexural rigidity (EI).
In this article, we’re going to discuss:
- Relation between supports of real and conjugate beam:
- Other conversions from real to conjugate beam:
- How to draw conjugate beam:
- How to solve the conjugate beam:
- Conjugate beam method examples:
Relation between supports of real and conjugate beam:
To draw the conjugate beam, it is necessary to know the conversions of supports from the real beam to the conjugate beam.
Here we have mentioned the conversions of supports done while drawing the conjugate beam:
| Sr. No. | Real Beam | Conjugate beam |
|---|---|---|
| 1 | Fixed support | Free end |
| 2 | Free end | Fixed support |
| 3 | Internal hinge/ Internal roller | Interior roller support/ Interior pin support |
| 4 | Interior roller support/ Interior pin support | Internal hinge/ Internal roller |
| 5 | Roller support/ Pin support | Roller support/ Pin support |
Other conversions from real to conjugate beam:
i) Loading for conjugate beam: The ratio of bending moment of the real beam to the flexural rigidity is considered as loading in the case of a conjugate beam.
E.g.: If the bending moment at a certain point of the real beam is ‘M’ then the load on the conjugate beam on that point is taken as (M / EI).
ii) Shear force at a certain point in the conjugate beam (V conjugate) is equal to the slope (𝚹 real) at that point in a real beam.
iii) Bending moment at a certain point in conjugate beam (M conjugate) is equal to the deflection (X real) at that point in a real beam
How to draw conjugate beam:
Here are the steps used to draw the conjugate beam from the real beam:
- Step 1: Draw the bending moment diagram for the real beam.
- Step 2: Divide the magnitudes of bending moments by flexural rigidity and draw the M/EI diagram.
- Step 3: Draw the conjugate beam having the same length as a real beam.
- Step 4: Plot the loading same as the M/EI diagram in step 2.
- Step 5: Apply the supports to the conjugate diagram as described before.
How to solve the conjugate beam:
Here are the steps used to solve the conjugate beam.
- Step 1: Find the reactions of the conjugate beam using equilibrium conditions.
- Step 2: Construct the shear force diagram for the conjugate beam. The values of the shear force in the conjugate beam diagram give the slope values in the real beam.
- Step 3: Construct the bending moment diagram for the conjugate beam. The values of the bending moment in the conjugate beam diagram give the deflection values in the real beam.
Conjugate beam method examples:
The numerical below will help you to understand the conjugate beam method easily.
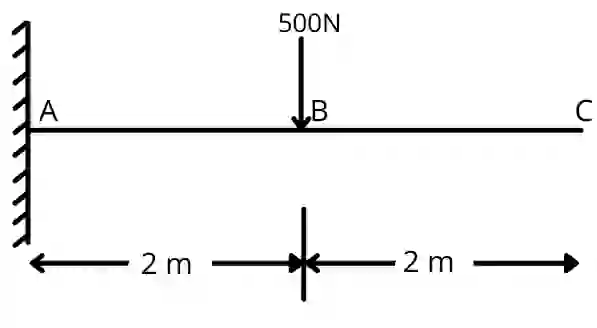
For the following beam calculate the slope and deflections at all points by the conjugate beam method. The beam has flexural rigidity, EI = 1.5 x 10⁶ N.m².
EI = 1.5 x 10⁶
Solution:
Step 1] Support reaction of real beam
By applying equation condition,
i] ΣFy = 0 [Take upward positive]
`R_{A}-500=0`
`R_{A}=500N` [Upward]
ii] `\sum M_{aA}=0` [Take clockwise positive]
[500 x 2]- MA = 0
MA = 1000 N.m
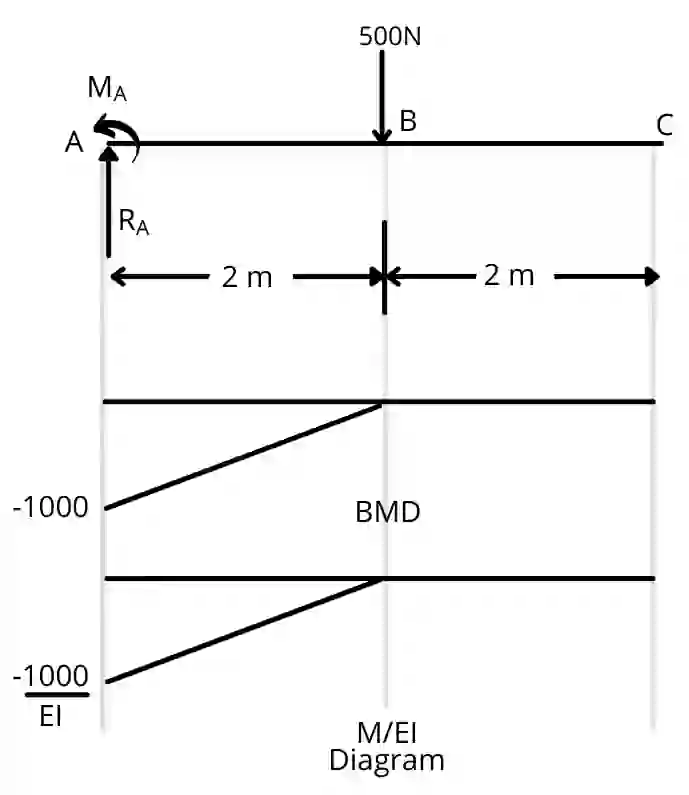
Step 2] Draw bending moment diagram:
calculate bending moments from A to C & consider clockwise moment as positive.
Note: JL= Just left, JR = Just right
`BM_{A_{JL}}`= 0 Nm
`BM_{A_{JR}}=-M_{A}`= -1000 Nm
`BM_{B}=-M_{A}+(R_{A}\times 2)`
`BM_{B}=-1000+(500\times 2)`
`BM_{B}` = 0 N.m.
`BM_{C}=(R_{A}\times 4)-M_{A}-(500\times 2)`
`BM_{C}=(500\times 4)-1000-(500\times 2)`
`BM_{C}` = 0 N.m.
Step 3] Draw M/EI diagram:
Divide the moment at each point by EI to draw the M/EI diagram.
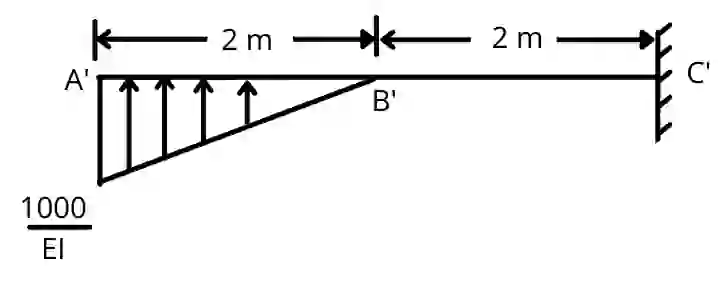
Step 4] Draw conjugate beam diagram
Draw the beam A’B’C’ of the same length as real beam.
Apply the conjugate supports as discussed above.
∴ The fixed support at A is replaced by open end and the open end at C is replaced by fixed support.
Apply the load as the M/EI diagram.
Step 5] Find support reactions of conjugate beam.
Apply equilibrium conditions to find the reactions.
1] `\sum F_{y}=0` [Consider upward force as positive]
`(\frac{100}{EI})-C_{y}=0`
`C_{y}=\frac{1000}{EI}`
2] `\sum M_{C}=0` [Consider clockwise moments positive]
`[\frac{1000}{EI}\times 3.33]-M_{C}=0`
`M_{C}=\frac{3330}{EI}`
Steps 6] Calculate the shear forces at all points of conjugate beam:
Calculate from end A to end C and Consider upward force as positive.
`SF_{A}=0`
`SF_{B}=\frac{1000}{EI}`
`SF_{C_{JL}}=\frac{1000}{EI}`
`SF_{C_{JR}}=\frac{1000}{EI}-\frac{1000}{EI}=0`
Step 7] Calculate bending moment at all points of conjugate beam:
`BM_{A}=0`
`BM_{B}=[\frac{1000}{EI}\times 1.33]`
`BM_{B}=\frac{1330}{EI}`
`BM_{C_{JL}}=[\frac{1000}{EI}\times 3.33]=\frac{3330}{EI}`
`BM_{C_{JR}}=[\frac{1000}{EI}\times 3.33]-M_{C}`
`BM_{C_{JR}}=0`
Step 8] Draw the SFD and BMD for the conjugate beam:
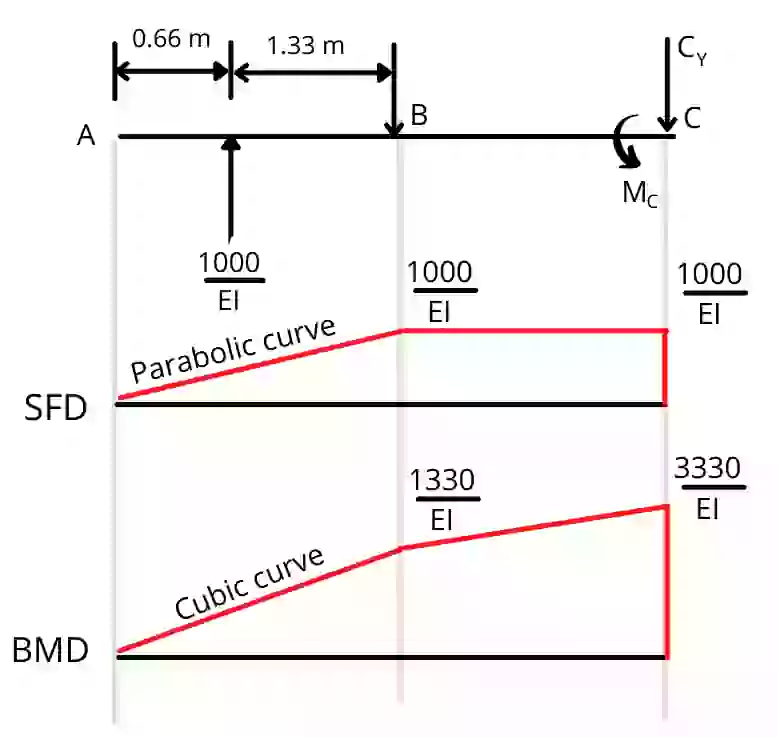
Step 9] Find slope and deflections of different points.
The values of shear force and bending moment in SFD and BMD give slope and deflection respectively.
At point A:
Slope `\theta _{A}=0`
Deflection `X_{A}=0`
At point B:
Slope, `\theta _{B}=\frac{1000}{EI}=\frac{1000}{1.5\times 10^{6}}=6.66\times 10^{-4}` radian
Deflection `X_{B}=\frac{1330}{EI}=\frac{1330}{1.5\times 10^{6}}=8.86\times 10^{-4}` m
At point C:
Slope, `\theta _{C}=\frac{1000}{EI}=\frac{1000}{1.5\times 10^{6}}=6.66\times 10^{-4}` radian
Deflection `X_{C}=\frac{3330}{EI}=\frac{3330}{1.5\times 10^{6}}=2.22\times 10^{-3}` m
Read also these articles: