Flexural rigidity: Definition, Formula, Unit, Significance

The term flexural rigidity is an important factor while the design of beams. Therefore in this article, we have tried to explain flexural rigidity along with its importance and numerical.

In this article, we’re going to discuss:

• What is Flexural rigidity?
• Flexural rigidity formula:
• Units of Flexural rigidity:
• Significances of Flexural rigidity:
• Flexural rigidity vs Torsional rigidity:
• Solved examples:
• FAQ’s:

What is Flexural rigidity?

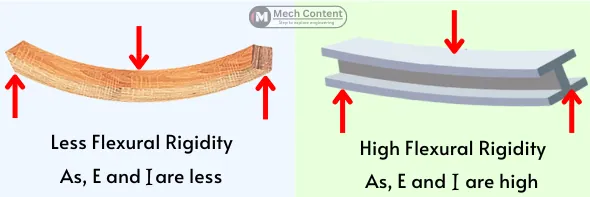
The flexural rigidity is the product of the modulus of elasticity (E) and moment of inertia (I) of the beam about the neutral axis. As we increase the value of flexural rigidity, the strength of the beam to resist bending also increases.

Flexural Rigidity = E x I

The flexural rigidity of components can be increased by raising the moment of inertia of the cross-section or by choosing the material with a higher modulus of elasticity.

Flexural rigidity formula:

The flexural rigidity is given by,

F.R. = E × I

Where,
E = modulus of elasticity of the material
I = Moment of Inertia at the neutral axis

As per the bending equation,

`\frac{E}{R} = \frac{M}{I}`

E × I = M × R

therefore the flexural rigidity is also given by,

F.R. = M × R

Where,
M = Bending moment
R = radius of curvature

Units of Flexural rigidity:

The SI unit of the modulus of elasticity is N/m² and the SI unit of moment of inertia is m⁴. Therefore the SI unit of flexural rigidity (FR) can be derived as,

F.R. = E x I = (N/m²) x (m⁴) = N.m²

Hence the SI unit is N.m². While the FPS unit of flexural rigidity is lb.ft².

It is also denoted by the unit Pa.m⁴.

Significances of Flexural rigidity:

The significances are as follows:-

1. The resistance of the beam for the bending depends on flexural rigidity.
2. The beam with a higher value of flexural rigidity has less value of deflection.

Flexural rigidity vs Torsional rigidity:

Sr. No.	Flexural Rigidity	Torsional Rigidity
1	It indicates the resistance offered by the beam to Bending.	It indicates the resistance of an object to twisting.
2	It is considered when the object is subjected to a bending load.	Torsional rigidity is considered when the object is subjected to the torsional or twisting load.
3	It depends on the modulus of elasticity (E) and moment of inertia (I).	It depends on shear modulus (G) and polar moment of inertia (J).

Solved examples:

1] Find the flexural rigidity of the beam if the beam is made of timber with a modulus of elasticity of 13 GPa and a moment of inertia of 5.2 x 10^-3 m⁴.

Solution:

Given:-
Modulus of elasticity, E = 13 GPa = 13 x 10⁹ N/m²
Moment of inertia, I = 5.2 x 10^-3 m⁴

The flexural rigidity of the beam is,

FR = E x I

= (13 x 10⁹) x (5.2 x 10^-3)

= 67.6 x 10⁶ Nm²

FAQ’s:

Read also:

• Bending stiffness explained