What is Bending stiffness?
The Bending stiffness is the resistance offered by a body against bending. It depends on the modulus of elasticity and the area moment of inertia of the object. As we increase the value of bending stiffness, the strength of an object to resist bending stress also increases.
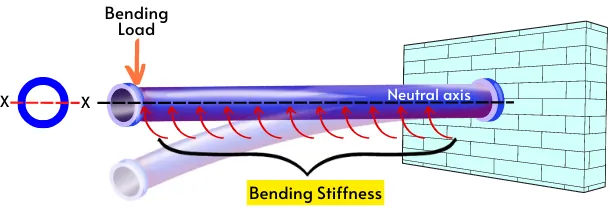
Object with high bending stiffness deflects less during the application of bending load.
The bending stiffness of the object can be increased with an increase in the Modulus of elasticity (E) and Moment of inertia (I).
In this article:
Formula of the Bending stiffness:
The formula is given by,
B.S. = Modulus of elasticity x Moment of inertia
B.S. = E x I
Units of the Bending stiffness:
The SI and FPS units are as follows:
In SI unit:
In the SI system, the unit of modulus of elasticity is N/m² and the unit of moment of inertia is m4 therefore the unit of B.S. is given by,
`= E × I = [\frac{N}{m^{2}}\times m^{4}]=N.m^{2}`
Therefore, the SI unit of B.S. is N.m2.
In FPS unit:
In the FPS system, the unit of modulus of elasticity is lb/ ft2 while the unit of moment of inertia is ft4. Hence the unit of B.S. is given by,
`= E × I = [\frac{lb}{ft^{2}}\times ft^{4}]=lb.ft^{2}`
Therefore, the FPS unit of B.S. is lb.ft2.
How to calculate bending stiffness?
These are the steps to find the B.S. of the object.
- Find the centroid of the cross-section of the object.
- Identify the neutral plane of the object based on the direction of the bending load (The neutral plane is perpendicular to the bending load).
- Find the second moment of area of the cross-section about the centroidal axis (parallel to the neutral plane).
- Find the modulus of elasticity of the material of the beam.
- Find bending stiffness, BS = `E \times I`
Beam bending stiffness:
The bending stiffness of the beam is also known as the flexural rigidity of the beam.
The bending stiffness of the beam at any point is given by the product of the modulus of elasticity and moment of inertia about a neutral axis at that point.
Examples:
1] Find the bending stiffness of the lever with a modulus of elasticity of 210 GPa and with a hollow circular cross-section.
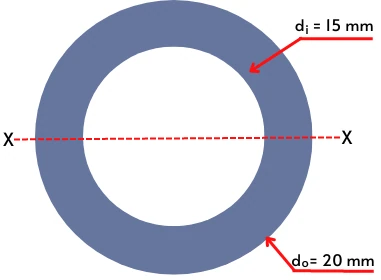
Given:
E = 210 Gpa = 210 × 103 N/m2
di = 15 mm
do = 20 mm
Solution:
The moment of inertia of a hollow circle about a centroidal axis is given by,
`I = \frac{\pi}{64}[d_{i}^{4}-d_{o}^{4}]`
`I = \frac{\pi}{64}[20^{4}-15^{4}]`
`I` = 5368.932 mm4
The B.S. in the lever is given by,
`B.S. = E \times I = [210 \times 10^{3}] \times5368.932`
B.S. = 1.127 × 109 N.mm2
2] The pullups bar has a modulus of elasticity of 120 GPa, find the bending stiffness of the bar.
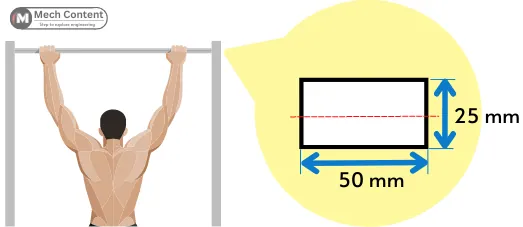
Given:
E = 120 GPa = 120 × 103 N/mm2
Solution:
The moment of inertia of a rectangular cross-section about a centroidal axis is given by,
`I = \frac{bd^{3}}{12}`
`I = \frac{50\times25^{3}}{12}`
`I` = = 65104.166 mm4
The B.S. is given by,
`B.S. = E\timesI`
`B.S. = [120\times10^{3}]\times[65104.166]`
B.S. = 7.812 × 109 N.mm2
FAQs:
-
What factors influence bending stiffness?
Bending stiffness is affected by the shape of the cross-section and the elastic modulus of the material.
-
Why is bending stiffness important?
Bending stiffness decides the ability of the object to resist deflection due to bending.
-
What exactly does a high bending stiffness mean?
The higher bending stiffness means less bending deflection in the object.