What is the Modulus of elasticity or Young’s modulus?
Modulus of elasticity for the elastic material is the ratio of longitudinal stress to the longitudinal strain. The modulus of elasticity is also known as Young’s modulus, named after scientist Thomas young.
The modulus of elasticity shows the stiffness of the material to resist axial deformation. It is the slope of the stress-strain curve up to the proportionality limit.
The modulus of elasticity is one of the four elastic constants. While others are the Modulus of rigidity (G), Bulk modulus (K), and Poisson’s ratio (`\nu`).
The modulus of elasticity states the relation between longitudinal stress applied and the strain developed in material up to the proportionality limit.
The modulus of elasticity is denoted by the symbol ‘E’.
Let’s see more about this in detail.
Contents:
Modulus of elasticity explained:
According to Hooke’s law, the stress applied to the material is directly proportional to the strain within the elastic limit.
The profile of the stress-strain curve is shown below.
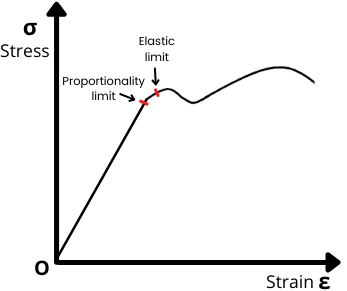
Up to the proportionality limit,
σ ∝ ε
σ = E x ε
Where E is constant which is known as the Modulus of elasticity and the value of E is constant up to the proportional limit.
Therefore it can be find as,
E = `\frac{\sigma}{\varepsilon}`
Modulus of elasticity formula:
As per the definition, the modulus of elasticity is given by,
E = `\frac{\text{Longitudinal stress}}{\text{Longitudinal strain}}`=`\frac{\sigma}{\varepsilon}`
Where,
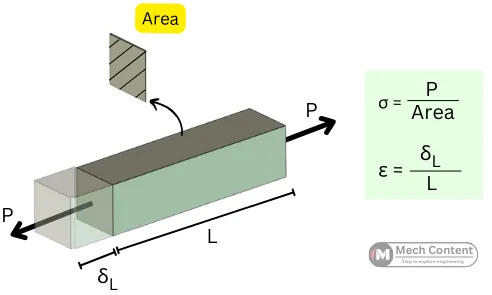
`\text{Longitudinal stress}` = `\frac{\text{Force}}{\text{Area}}`
`\text{Longitudinal strain}` = `\frac{\text{Change in length}(\delta_{L})}{\text{Original length (L)}}`
Modulus of elasticity units:
SI unit:-
In the SI system, the unit of longitudinal stress is N/m² or Pascal and the longitudinal strain is a unitless quantity.
∴ E = `\frac{\sigma}{\varepsilon}` = N/m²
Therefore the SI unit of modulus of elasticity is N/m² or Pascal.
FPS unit:-
In the FPS system, the unit of longitudinal stress is lb/ft² and the strain is a unitless quantity.
∴ E = `\frac{\sigma}{\varepsilon}` = lb/ft²
Therefore FPS unit of modulus of elasticity is lb/ft².
Modulus of elasticity dimensional formula:
The dimensional formula of stress is given by [ML⁻¹T⁻²].
The strain is the unitless quantity therefore for the strain, the dimensional formula is [M⁰L⁰T⁰].
Therefore the dimensional formula is,
E = `\frac{\sigma}{\varepsilon}` = `\frac{[ML^{-1}T^{-2}]}{[M^{0}L^{0}T^{0}]}` = [ML⁻¹T⁻²]
Therefore for the modulus of elasticity, the dimensional formula is [ML⁻¹T⁻²].
How to calculate modulus of elasticity?
Following are the different ways to find the modulus of elasticity:-
A) If the values of stress and the corresponding strain are known then the modulus of elasticity can be calculated by using the following formula:-
E = `\frac{\text{Longitudinal stress}(\sigma)}{\text{Longitudinal strain}(\varepsilon)}`
B) If the graph of the stress-strain curve is available, then in this case the slope of the stress-strain curve gives the modulus of elasticity for that material.
C) By performing the experiment using Searle’s apparatus, the modulus of elasticity can be find for the given elastic material.
How to calculate modulus of elasticity from stress-strain curve?
Up to the elastic limit, the stress is directly proportional to strain. The slope of the stress-strain curve up to the proportionality limit gives the modulus of elasticity.
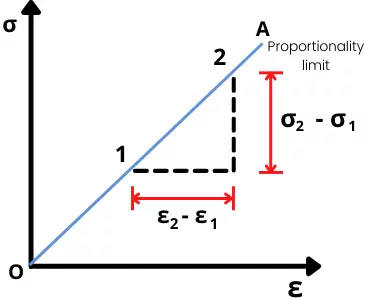
Thus from the above stress-strain diagram,
E = Slope of OA = `\mathbf{\frac{\sigma_{2}-\sigma_{1}}{\varepsilon_{2}-\varepsilon_{1}}}`
How to find modulus of elasticity? (Experimental method)
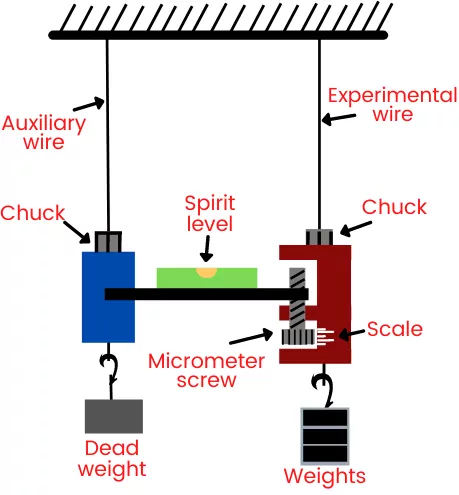
The modulus of elasticity of the material can be calculated by using Searle’s apparatus experiment.
Searle’s experimental setup helps to find the elongation in the experimental wire by keeping the auxiliary wire as a reference.
The spirit level arrangement and micrometer help to find the elongation in the experimental wire with reference to the auxiliary wire.
Following are the steps to perform the experiment on Searle’s apparatus to find the modulus of elasticity:-
- Hang the Searle’s apparatus to the auxiliary wire and experimental wire by using a chuck.
- Add dead weight to the auxiliary wire and weight hanger to the experimental wire. Note down the diameter of the wire and the length of the wire.
- Adjust the bubble of spirit level by adjusting the micrometer screw and measure the reading on the scale of a micrometer.
- Add single weight to the weight hanger.
- After adding the weight, the experimental wire extends and the level on the spirit level gets disturbed.
- Adjust the bubble of spirit level by adjusting the micrometer screw and measure the reading on the scale of a micrometer.
- Similarly, increase weight one by one and find the elongation occured in the wire.
- After performing the experiment, plot the reading of the extension in observation table and find the value of modulus of elasticity. Following is the example of the observation table that will help you to find the modulus of elasticity.
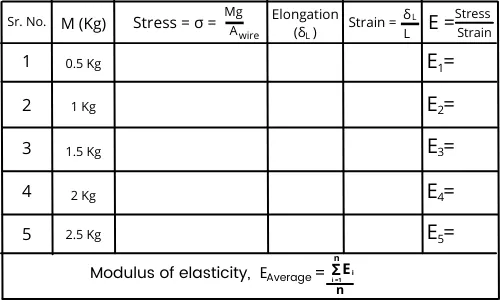
Where,
`A_{wire}` = Cross-sectional area of the wire = `\frac{\pi}{4}\times d^{2}`
`δ_{L}` = Change in the length of wire
By using this table, you can mathematically calculate the modulus of elasticity of wire material.
- We can also plot the readings of the stress and strain obtained by experiment on the stress-strain curve as shown in the below figure,
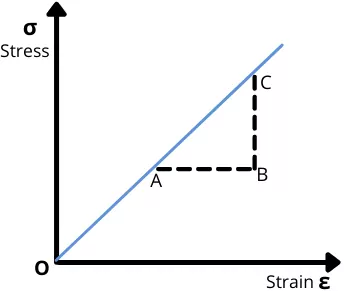
- Even by finding the slope of this stress-strain curve we can find the modulus of elasticity.
E = Slope = `\frac{CB}{AB}`
Modulus of elasticity examples:
The aluminum rod of diameter 10 mm and length of 1000 mm is loaded with a load of 27 KN. If the elongation in the rod is 5 mm, then find the modulus of elasticity of the aluminum rod.
Given:
D = 10 mm
L = 1000 mm
P = 27 KN = 27000 N
`\delta_{L}` = 5 mm
Solution:–
The stress on the aluminum rod is given by,
σ = `\frac{P}{Area}`
σ = `\frac{P}{\frac{\pi}{4} \times D^{2}}`
σ = `\frac{27000}{\frac{\pi}{4} \times 10^{2}}`
σ = 343.774 N/mm²
The strain occurred in the aluminum rod is given by,
ε = `\frac{\delta_{L}}{L}`
ε = `\frac{5}{1000}`
ε = 0.005
The modulus of elasticity for the material is given by,
E = `\frac{\sigma}{\varepsilon}`
E = `\frac{343.774}{0.005}`
E = 68754 N/mm²
Therefore the modulus of elasticity of the aluminum rod is 68754 N/mm².
FAQ’s:
-
What is modulus of elasticity of a material?
Modulus of elasticity is the ratio of stress to the corresponding strain up to the elastic limit.
-
What is the SI unit of modulus of elasticity?
In the SI unit system, the modulus of elasticity has a unit of Pascal or N/m².
-
What is the difference between Young’s modulus and modulus of elasticity?
There is no such difference between the terms Modulus of Elasticity and Young’s modulus. The modulus of elasticity of also known as young’s modulus.
-
Is modulus of elasticity the same as modulus of rigidity?
No, The modulus of elasticity is the ratio of longitudinal stress to the longitudinal strain while the modulus of rigidity is the ratio of shear stress to shear strain.
-
What is another name for modulus of elasticity?
The modulus of elasticity is also known as Young’s modulus, named after the British scientist Thomas young.
-
What is the dimension formula of modulus of elasticity?
For the modulus of elasticity, the dimensional formula is [ML⁻¹T⁻²].
-
How does modulus of elasticity vary with temperature?
The modulus of elasticity of material decreases with an increase in temperature because of the increase in lattice vibration in the material.
-
What is the symbol of modulus of elasticity?
The modulus of elasticity is generally denoted by the symbol ‘E’.
