The steam turbine efficiency is calculated in terms of the blade efficiency and/or the stage efficiency calculated by using the velocity diagram of the moving blade.
Contents:
Steam turbine efficiency:
The efficiency of the steam turbine is the ability of the turbine to extract the energy from the steam and convert it into useful work.
The efficiency of the steam turbine is the ratio of work output at the turbine rotor to the energy supplied by the steam to the turbine.
`\eta_{T}` = `\frac{\text{Work}}{\text{Energy supplied}}`
The efficiency of the steam turbine depends on various factors like inlet velocity of steam, inlet and exit blades angles, the radius of the moving blade ring, etc.
The steam turbine has two types of efficiencies as follows:-
- Blade efficiency or diagram efficiency
- Stage efficiency
Steam turbine efficiency calculation:
For different types of steam turbines (Impulse & Reaction), the calculation for the efficiency is discussed below:-
1] For impulse turbine:-
The below figure shows the velocity diagram for the moving blade of impulse turbine.
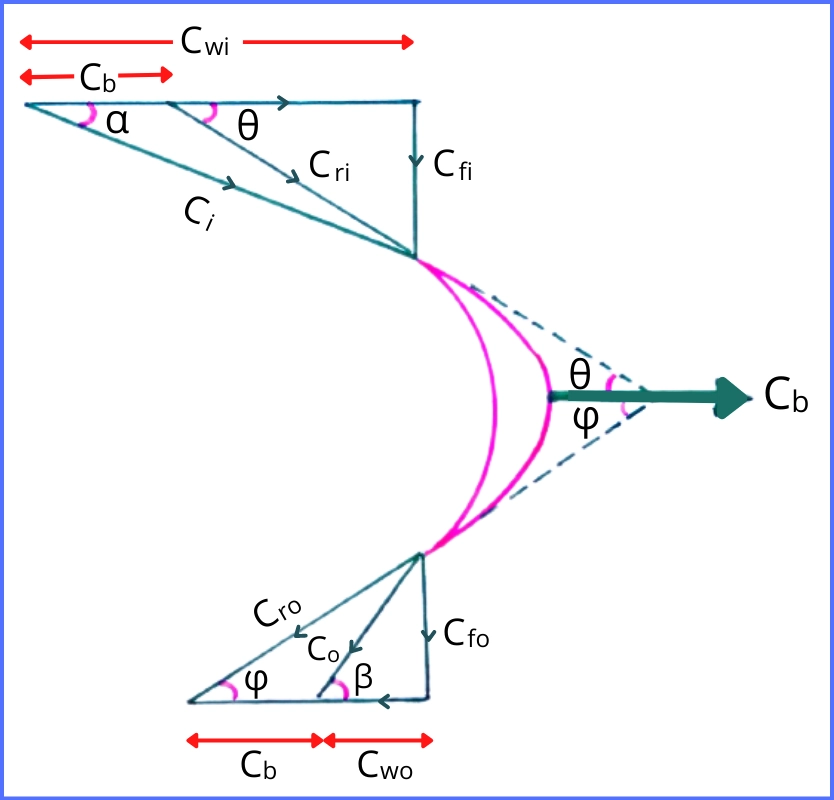
Where,
`C_{b}` = Blade velocity
`C_{i}` = Inlet velocity of steam
`C_{o}` = Exit velocity of steam
`C_{\text{wi}}` = Whirl velocity at inlet
`C_{\text{wo}}` = Whirl velocity at the exit
`C_{\text{fi}}` = Flow velocity at inlet
`C_{\text{fo}}` = Flow velocity at exit
`C_{\text{ri}}` = Relative velocity at inlet
`C_{\text{ro}}` = Relative velocity at exit
θ = Moving blade inlet angle
φ = Moving blade exit angle
α = Angle of steam inlet
β = Angle of steam exit
The force applied by steam on the blade in the direction of blade is given by,
F = Change in momentum in the direction of the blade.
F = ṁ (Change in whirl velocity)
F = ṁ [`C_{\text{wi}}-C_{\text{wo}}`]
F = ṁ [`C_{\text{wi}}-(-C_{\text{wo}})`] ———- (∵ `C_{\text{wo}}` moves in opposite direction )
F = ṁ [`\mathbf{C_{\text{wi}}+C_{\text{wo}}}`]
Now the work done by steam on the moving blade is given by,
W = Force x blade velocity
W = F x `C_{b}`
W = ṁ`\mathbf{[C_{\text{wi}}+C_{\text{wo}}].C_{b}}`
The total whirl velocity can be given by,
`C_{\text{w}}` = `C_{\text{wi}}+C_{\text{wo}}`
Therefore the equation of work will become,
W = ṁ.`\mathbf{C_{w}.C_{b}}`
Now the blade efficiency of the impulse turbine is given by,
Blade efficiency, `\eta_{b}` = `\frac{\text{Workdone}}{\text{Energy supplied}}`
The energy supplied to the blade is equal to the kinetic energy of steam.
∴ Energy supplied = `\mathbf{\frac{1}{2} \dot{m}. C_{i}^{2}}`
Thus the blade efficiency will become,
`\eta_{b}` = `\frac{\dot{m}C_{w}C_{b}}{\frac{1}{2}\dot{m}C_{i}^{2}}`
| `\mathbf{\eta_{b}}` = `\mathbf{\frac{2C_{w}C_{b}}{C_{i}^{2}}}` |
This is the equation of blade efficiency for the impulse steam turbine.
The stage efficiency of the impulse turbine is given by, the ratio of workdone to the enthalpy drop into the nozzle.
Stage efficiency, `\eta_{\text{stage}}` = `\frac{\text{Workdone}(W)}{\text{Enthalpy drop}(\Delta H)}`
`\eta_{\text{stage}}` = `\frac{\dot{m}.C_{w}C_{b}}{\dot{m}.\Delta h}`
| `\mathbf{\eta_{\text{stage}}}` = `\mathbf{\frac{C_{w}C_{b}}{\Delta h}}` |
This is the equation of stage efficiency of the impulse turbine.
The stage efficiency can also be given by,
| `\mathbf{\eta_{\text{stage}}}` = `\mathbf{\eta_{n}\times\eta_{b}}` |
Where,
`\eta_{n}`= Nozzle efficiency
`\eta_{b}`= Blade efficiency
2] For Reaction turbine:-
The below figure shows the velocity diagram for the moving blade of the reaction turbine.
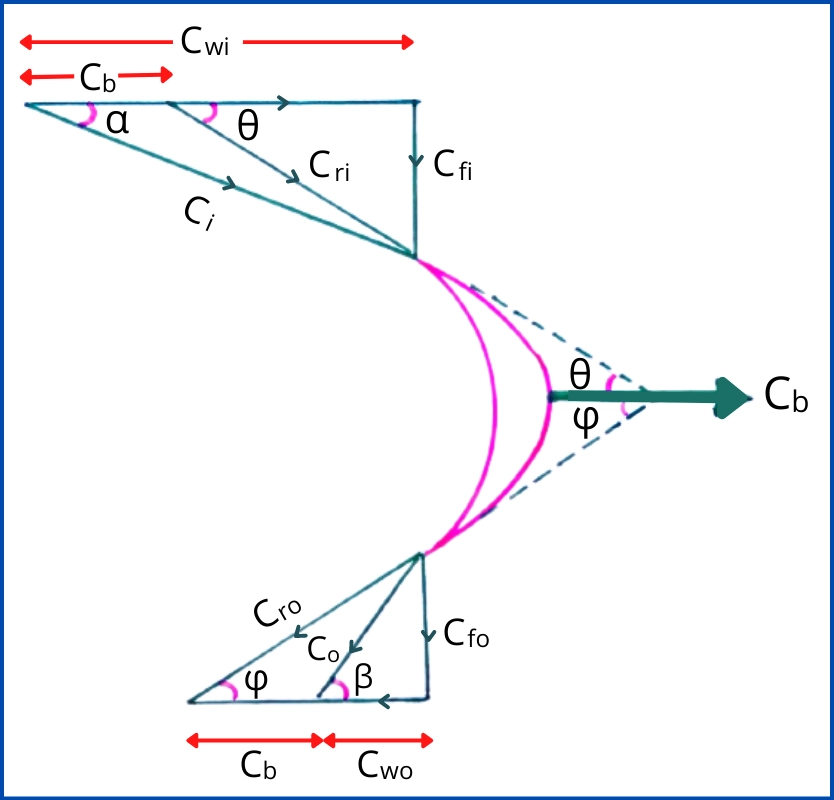
The work done by the steam on the moving blade is given by,
W = `\mathbf{\dot{m}.(C_{wi} + C_{wo}).C_{b}}`
The energy supplied by the steam is given by,
E = `\mathbf{\dot{m}(\frac{C_{i}^{2}}{2} + \frac{C_{ro}^{2}-C_{ri}^{2}}{2})}`
Now the blade efficiency for the reaction turbine is given as,
`\eta_{blade}` = `\frac{\text{Workdone} (W)}{\text{Energy supplied}(E)}`
`\eta_{blade}` = `\frac{\dot{m}.(C_{wi} + C_{wo}).C_{b}}{\dot{m}(\frac{C_{i}^{2}}{2}+\frac{C_{ro}^{2}-C_{ri}^{2}}{2})}`
`\eta_{blade}` = `\frac{(C_{wi} + C_{wo}).C_{b}}{(\frac{C_{i}^{2}}{2}+\frac{C_{ro}^{2}-C_{ri}^{2}}{2})}`
| `\mathbf{\eta_{blade}}` = `\mathbf{\frac{2.(C_{wi} + C_{wo}).C_{b}}{C_{i}^{2}+(C_{ro}^{2}-C_{ri}^{2})}}` |
This is the equation for the blade efficiency of a reaction turbine.
Steam turbine efficiency formula:
For impulse turbine:-
Blade efficiency:-
The blade efficiency of the impulse steam turbine is given by,
| `\eta_{b}` = `\frac{2.C_{w}.C_{b}}{C_{i}^{2}}` |
Where,
`C_{b}` = Blade velocity
`C_{i}` = Steam velocity at moving blade inlet
`C_{w}` = Total whirl velocity
Stage efficiency:-
The stage efficiency of the impulse turbine is given by,
| `\eta_{\text{stage}}` = `\frac{C_{w}.C_{B}}{\Delta h}` |
Where,
`\Delta h` = Enthalpy drop in the nozzle per Kg of steam
For reaction turbine:-
The blade efficiency for the reaction turbine is given as,
| `\eta_{blade}` = `\frac{2.(C_{wi} + C_{wo}).C_{b}}{C_{i}^{2}+(C_{ro}^{2}-C_{ri}^{2})}` |
Where,
`C_{ri}` = Inlet relative velocity
`C_{ro}` = Exit relative velocity
How to calculate steam turbine efficiency?
Following are the steps to find the blade or diagram efficiency and stage efficiency of the turbine:-
Step 1: Find the moving blade velocity (`C_{b}`), It can be evaluate by using following equation,
`C_{b}` = `\frac{\pi.d.N}{60}`
Where,
N = Speed of rotor in rpm
d = diameter of moving blade ring
Step 2: Draw the velocity diagram and find the total whirl velocity
Where total whirl velocity is given by,
`C_{w}` = `C_{wi}+C_{wo}`
Step 3: Find the blade efficiency by using the following formula,
`\eta_{b}` = `\frac{2.C_{w}.C_{B}}{C_{i}^{2}}`
Step 4: To find stage efficiency, first find the enthalpy drop of steam into the nozzle by using the steam properties.
Then by using the below formula find the stage efficiency of the impulse turbine
`\eta_{\text{stage}}` = `\frac{C_{w}.C_{B}}{\Delta.h}`