One of the key differences between centripetal acceleration and tangential acceleration is that centripetal acceleration is the radial component of the net acceleration and tangential acceleration is the tangential component of the net acceleration acting on the object moving in a circular direction.
Contents:
Centripetal acceleration (Radial acceleration):
It is the acceleration acting on the object performing circular motion which results due to the constant change in direction of tangential velocity of the object. It acts along the radius of rotation toward the center of rotation of the object.
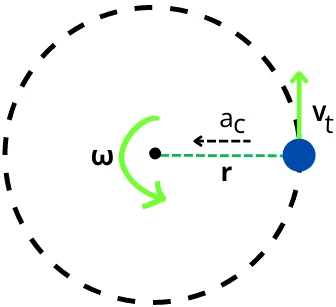
For the object shown in the above figure rotating at a radius of ‘r’ and at velocity `v_{t}`, the centripetal acceleration is given by,
`\mathbf{a_{c}}` = `\mathbf{a_{r}}` = `\mathbf{\frac{v_{t}^{2}}{r}}` = `\mathbf{r.\omega^{2}}`
Tangential acceleration:
In the case of an object undergoing circular motion, the rate of change of the tangential velocity of an object with respect to time is known as a tangential acceleration.
It is a linear term and measured in terms of m/s² or ft/s².
It always acts parallel to the tangential velocity vector and acts perpendicular to the radius vector.
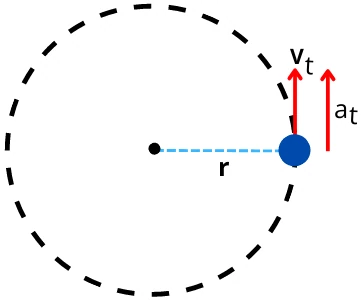
At any instant during the motion, the tangential acceleration on the object is given by,
`\mathbf{a_{t}}` = `\mathbf{\frac{dv_{t}}{dt}}`
Centripetal (Radial) vs Tangential acceleration:
| Sr. No. | Centripetal acceleration (Radial) | Tangential acceleration |
|---|---|---|
| 1 | It is the acceleration possessed by the object undergoing circular motion due to the constantly changing direction of tangential velocity of the object. | The tangential acceleration indicates a change in the tangential velocity of the object undergoing circular motion. |
| 2 | It occurs due to the change in direction of the tangential velocity. | It occurs due to the change in the magnitude of a tangential velocity. |
| 3 | It is always directed toward the center of rotation. | It always acts in a tangential direction to the circular path. |
| 4 | Centripetal acceleration is required for an object to move in a circular path. | The object can perform circular motion with zero tangential acceleration. |
| 5 | The centripetal acceleration is given by, `a_{c}` = `\frac{v_{t}^{2}}{r}` = `r\omega^{2}`. | The tangential acceleration is given by, `a_{t}` = `\frac{dv_{t}}{dt}`. |
| 6 | It is a radial component of the net acceleration of the object. | It is a tangential component of the net acceleration of the object. |
| 7 | The centripetal acceleration is denoted by `a_{c}` or `a_{r}`. | It is denoted by the symbol `a_{t}`. |
FAQs:
-
Are tangential and centripetal acceleration the same?
No, the tangential and centripetal acceleration are different but both are related to the object moving in a circular motion.
-
What is the difference between tangential and radial acceleration for a point on a rotating body?
For the rotating body, the tangential acceleration creates the tangential component of the object’s net acceleration, whereas the radial acceleration creates the radial component.
Related differences: