The first moment of area is just a product of the area of the lamina and the distance of its centroid from the axis. But it’s difficult when the shape becomes complex. Sometimes, the first moment of area is incorrectly referred to as a first moment of inertia.
To know in detail about its formula, units, how to find it, and solved numerals, read the full article.
Contents:
What is the First moment of area?
First moment of area about any reference axis is the product of the area of shape and distance between the centroid of shape and the reference axis. Finding the first moment of area is necessary while finding the centroid of the lamina and to find the transverse shear stress acting on the object.
First moment of area (Q) = Area of the shape (A) × Distance of reference axis from centroid (r)
The first moment of area is generally denoted by the symbol ‘Q’. It depends on the area of the shape and the distance of the reference axis from the centroidal axis.
The value of the Q is zero or minimum when the reference axis is at the centroid of the shape (distance = 0).
As the Q represents the product of terms area (m2) and length (m), it has unit of m3 in SI system and ft3 in FPS system.
First moment of area formula:
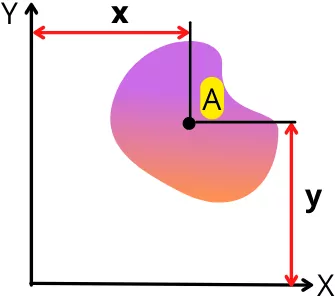
For the shape shown in the above figure, the 1st moment of area about the x-axis and y-axis is given by,
Qx = A x 𝓨
Qy = A x 𝓧
For complex shapes:
For a complex shape consisting of more than one simple geometric shape, the first moment of area is the summation of the product of the area of each section and the distance between its centroid from the reference axis.
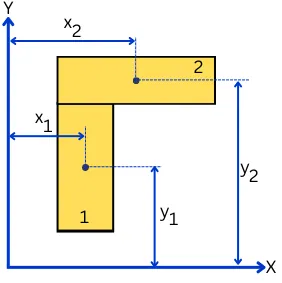
The 1st moment of area of the complex shape about any reference axis (X and Y) is given by,
Qx = Σ Ai 𝓨i
Qy = Σ Ai 𝓧i
Where,
A = Area of each shape
𝓧 or 𝓨 = Distance between the centroid of shape and reference axis (X or Y).
Considering the shape consist ‘n’ number of simple shapes, then the Q can be calculated as,
Qx = `\sum A_{i}y_{i}=A_{1}y_{1}+A_{2}y_{2}+\cdots + A_{n}y_{n}`
Qy = `\sum A_{i}x_{i}=A_{1}x_{1}+A_{2}x_{2}+\cdots+A_{n}x_{n}`
Where,
`A_{1}, A_{2}, A_{3}, \cdotsA_{n}` = Area of the each shape
`y_{1}, y_{2}, y_{3}, \cdots y_{n}` = Distance of the centroid of each shape from the x-axis
`x_{1}, x_{2}, x_{3}, \cdots x_{n}` = Distance of the centroid of each shape from the y-axis
First moment of area integral for irregular shapes:
The below figure shows the plane lamina with an irregular shape.
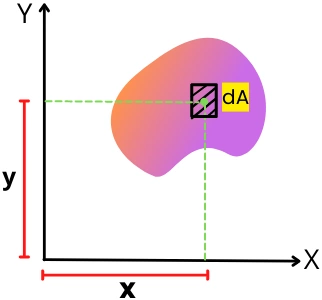
Consider a small elemental area dA with the centroid located at coordinate (x, y).
By the definition, the first moment of area of dA about the X and Y-axis is given by,
dQy = 𝓧. dA
dQx = 𝓨.dA
Integrate the dQy and dQx to find the first moment of area of total shape about the X and Y-axis,
Qy = ∫ 𝓧.dA
Qx = ∫ 𝓨.dA
How to calculate first moment of area?
Following are the steps to calculate the first moment of area of complex shapes:
Step 1] Divide the complex shape into simple geometric shapes as shown below.
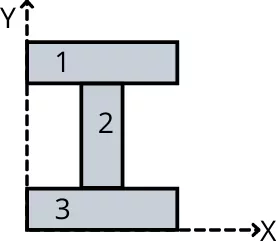
Step 2] Find the distance between the centroid and reference axis for each shape (𝓧1, 𝓧2, 𝓧3 or 𝓨1, 𝓨2, 𝓨3).
Step 3] Find the area of each shape (A1, A2, A3).
Step 4] Find the first moment of area using the following formulae,
For the above figure, the first moment of area about the 𝓧-axis is given by,
Qx = `\sum A_{i}y_{i}`
Qx = `A_{1}y_{1}+A_{2}y_{2} + A_{3}y_{3}`
For the above shape, the first moment of area about the 𝓨-axis is given by,
Qy = `\sum A_{i}x_{i}`
Qy `=A_{1}x_{1}+A_{2}x_{2}+A_{3}x_{3}`
When to use first moment of area?
The first moment of area is used for the following purpose:
1] To find the centroid of complex shapes:
For the complex shape consisting of different simple geometric shapes, the position of centroid from the X- axis (`\bar{Y}`) can be calculated as,
`\bar{Y}=\frac{\sum Q_{\text{xi}}}{A_{\text{Total}}}`
`\bar{Y}=\frac{Q_{x1} + Q_{x2} + \cdots + Q_{xn}}{A_{\text{Total}}}`
`\bar{Y}=\frac{A_{1}y_{1} + A_{2}y_{2} + \cdots + A_{n}y_{n}}{A_{\text{Total}}}`
Where,
`Q_{x1}, Q_{x2}, \cdots, Q_{xn}` = First moment of area of each shape about the X-axis
Atotal = Total area of complex shape
And the position of centroid from the Y-axis (`\bar{X}`) is given by,
`\bar{X}=\frac{\sum Q_{yi}}{A_{\text{Total}}}`
`\bar{X}=\frac{Q_{y1} + Q_{y2} + \cdots + Q_{yn}}{A_{\text{Total}}}`
`\bar{X}=\frac{A_{1}x_{1} + A_{2}x_{2} + \cdots + A_{n}x_{n}}{A_{\text{Total}}}`
Where,
`Q_{y1}, Q_{y2}, \cdots Q_{yn}` = First moment of area of each shape about the Y-axis
2] For the object subjected to the bending load, the first moment of area is necessary to find the transverse shear stress.
When first moment of area becomes zero?
At the centroidal axis, the first moment of area of the object becomes zero.
The first moment of area is the product of the area of the shape and the distance between the centroid of the shape and the reference axis.
Q = A`\times`𝓧
The centroidal axis passes through the centroid of the shape.
∴ 𝓧 = 0
Therefore, the first moment of area at the centroidal axis is,
Q = A x 0
∴ Q = 0
Q for different shapes:
The first moment of area for circle, hollow circle, and rectangle shape is given below:
1] For circle:
The below figure shows the circle with the centroid located at a distance of (x, y) from the origin of the axis.
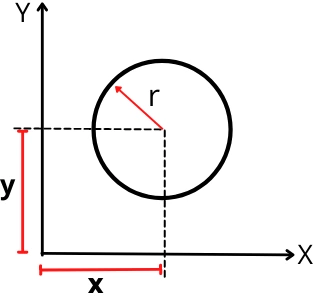
For the above circle, the first moment of area about the 𝓧-axis is given by,
Qx = A x 𝓨
As, area of the circle, A = π.r²
`\thereforeQ_{x}` = π.r² 𝓨
Similarly, the first moment of area about the 𝓨-axis is given by,
Qy = A x 𝓧
Qy = πr² 𝓧
2] For Hollow circle:
The below figure shows the hollow circular shape with the centroid located at a distance of (x, y) from the origin.
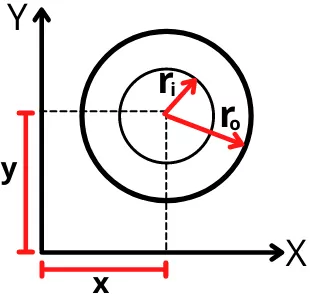
For the above hollow circle, the first moment of area about the 𝓧-axis is given by,
Qx = A x 𝓨
Qx = `(\pi.r_{o}^{2} – \pi.r_{i}^{2})` × 𝓨
Qx = `\pi.(r_{o}^{2} – r_{i}^{2})` × 𝓨
Similarly, the first moment of area of a circle about the 𝓨-axis is given by,
Qy = A × 𝓧
Qy = `(\pi.r_{o}^{2} – \pi.r_{i}^{2})` × 𝓧
`Q_{y}=\pi.(r_{o}^{2} – r_{i}^{2})` × 𝓧
3] For Rectangle:
The below figure shows the rectangle of width b and height d with the centroid located at a distance of (x, y) from the origin.
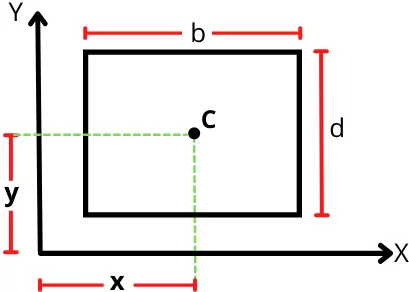
For the above rectangle, the first moment of area about the 𝓧-axis is given by,
Qx = A × 𝓨
Qx = bd × 𝓨
Similarly, the first moment of area of a rectangle about the 𝓨-axis is given by,
Qy = A × 𝓧
Qy = bd × 𝓧
First moment of area solved examples:
For the I beam shown below, find the first moment of area about the 𝓧-axis and the first moment of area of half-section about the neutral axis of beam.
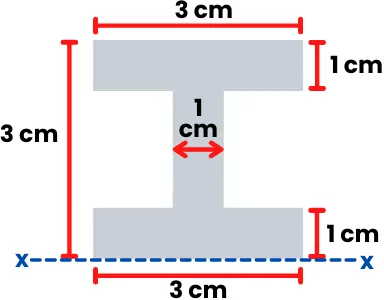
Solution:
1] First moment of area about x-axis:
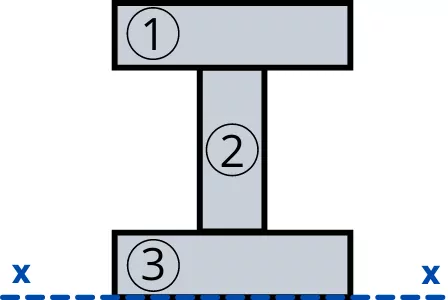
Divide the I-beam into simple geometric shapes. The area of each shape is given by,
A1 = 3 × 1 = 3 cm²
A2 = 1 × 1 = 1 cm²
A3 = 3 × 1 = 3 cm²
The position of the centroid of each shape from the x-axis is given by,
y1 = 2.5 cm
y2 = 1.5 cm
y3 = 0.5 cm
Now the first moment of area about the x-axis is given by,
Qx = `\sum A_{i}y_{i}`
Qx = A1y1 +A2y2 + A3y3
Qx = (3 × 2.5) + (1 × 1.5) + (3 × 0.5)
Qx = 10.5 cm3
2] First moment of area of half-section about a neutral axis:
Given I-beam is symmetric thus the neutral axis passes through the center of the I-beam.
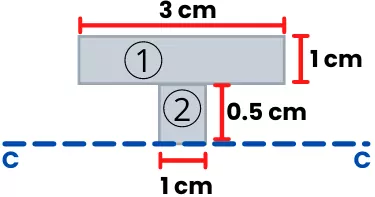
Now the area of each shape of the section is,
A1 = 3 × 1 = 3 cm2
A2 = 1 × 0.5 = 0.5 cm2
The distance between the centroid and neutral axis for each shape is given by,
y1 = 1 cm
y2 = 0.25 cm
Now the first moment of area of the upper half-section about a neutral axis is given by,
QC = `\sum A_{i}y_{i}`
QC = A1y1 + A2y2
QC = (3 × 1) + (0.5 × 0.25)
QC = 3.125 cm3
FAQs:
-
When does the first moment of area become negative?
It depends on the position of an axis. If the distance of the centroid of the shape from the axis is negative then the first moment of area also becomes negative.