Along with mass and height, the potential energy also depends on gravity. So in this article, we are going to look, How gravity affects potential energy in different conditions.
The acceleration due to gravity can vary in the following conditions: Over different locations on the same planet, Changing height from the surface of the planet, and Varies over different planets.
As gravitational acceleration varies over the position of the object, it also causes changes in potential energy experienced by the object.
Gravitational potential energy (P.E.) is directly proportional to gravitational acceleration (g) in case of variation of ‘g’ over various locations on Earth and the variation of ‘g’ among different planets. But P.E. is inversely proportional to ‘g’ in case of variation of ‘g’ while changing height from the planet surface.
Thus let’s check, how potential energy is affected by changing gravity in different cases.
Contents:
Due to varying gravity in different regions on the same planet:
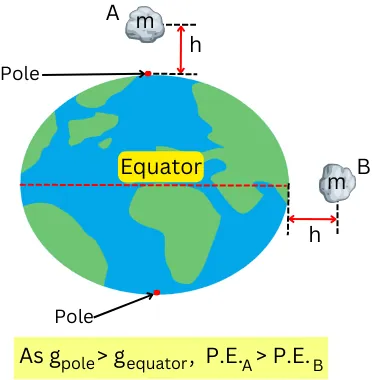
The value for ‘g’ rises gradually from the equator to the poles. Gravitational acceleration (g) is maximum at the poles and minimum at the equator. Since the poles are closer to the center of the earth than the equator.
Such changing value of ‘g’ has an effect on the potential energy of an object.
As the value of ‘g’ over the surface of the earth increases, the P.E. acting on the object also increases.
Example:
If we raise the same object at the same height at the pole and the equator, then the object at the pole possesses high potential energy than the equator.
Different gravities over different planets:
The value for the gravitational acceleration (g) is different for the various planets. Therefore as `P.E. \propto g`, the potential energy is also different over the different planets.
Let me explain with an example.
Consider planets A and B, with planet A having higher gravitational acceleration than planet B (gA > gB).
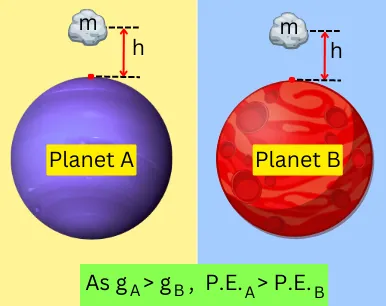
Consider two objects of the same mass raised at the same height from the surface of both planets A and B.
As, P.E. ∝ g & gA > gB, therefore the object raised on planet A will experience higher potential energy than the object on planet B.
Due to varying gravity by the height of the object:
The value for the gravitational acceleration is given by,
`g = \frac{GM}{R + h^{2}}\cdots \text{[1]}`
Where,
G = Gravitational constant
M = Mass of the planet/larger object
R = Radius of the planet
h = Height of the smaller object from the surface of the planet
From the above equation, we can say that the gravitational acceleration (g) decreases as the height (h) from the surface increases.
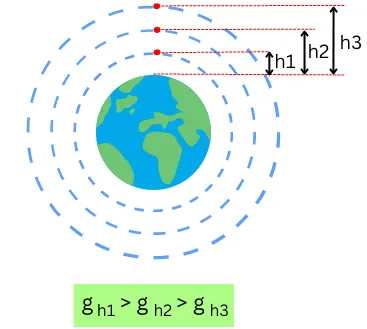
But does a decreasing gravitational acceleration (g) cause P.E. to decrease? Let’s discuss it.
The P.E. of the object relative to the ground surface is given by,
P.E. = mgh
`P.E. = m. [\frac{GM}{R + h^{2}}]. h\cdots\text{[From [1]]}`
As G, M, and m are constant,
`PE \propto \frac{h}{(R+h)^{2}}`
`PE\propto\frac{1}{\frac{(R+h)^{2}}{h}}`
`PE\propto\frac{1}{\frac{R^{2}}{h}+2R+h}`
As h<<R (Radius of the planet is comparatively higher than the object’s height from planet surface),
`\thereforePE\propto\frac{1}{\frac{R^{2}}{h}+2R}`
From the above equation, as ‘h’ increases, `\frac{R^{2}}{h}` decreases, and `\frac{1}{\frac{R^{2}}{h}+2R}` gets increases. Thus the potential energy increases.
Thus the lowering of ‘g’ (due to increasing height) causes the Potential energy of the object to increase. This is because, height itself has more effect on PE than changing gravitational acceleration (due to changing height).
Read also: