The moment of inertia of the rod about any particular axis indicates the tendency of the rod to resist the angular acceleration about that axis.
Here the rod is considered a thin uniform rod. The uniform rod indicates the rod has the same linear mass density (mass/length) at any portion of the rod.
The value of the moment of inertia of the rod depends on the mass and length of the rod and the position of the axis where the moment of inertia needs to be measured.
Below we will discuss and derive the formulae for different cases of the moment of inertia of a rod.
Contents:
Different formulae for Moment of inertia of a rod:
For Rod:
For the rod of mass ‘M’ and length ‘L’, the equations for the moment of inertia about different axis positions are as follows:-
A] Axis passing through center and perpendicular to rod:
`I = \frac{M.L^{2}}{12}`
B] Axis passing through end and perpendicular to the rod:
`I = \frac{M.L^{2}}{3}`
C] Axis parallel to the rod at a distance of x:
The moment of inertia of a rod about an axis parallel to the rod at a distance of ‘x’ is given by,
`I = M.x^{2}`
For Rod with Point mass:
A] Point mass at one end:
In this case, the thin rod of mass ‘M’ and length ‘L’, has a point mass ‘m1‘ attached at one end.
The moment of inertia about an axis at the other end and perpendicular to the rod is given by,
`\mathbf{I_{C-C’}= \frac{M.L^{2}}{3} + m_{1}.L^{2}}`
The moment of inertia about a perpendicular axis passing through the center of the rod is given by,
`\mathbf{I_{O-O’} = \frac{M.L^{2}}{12} + \frac{m_{1}.L^{2}}{4}}`
B] Point mass at both ends:
In this case, two point masses m1 and m2 are attached at the ends of the rod.
The moment of inertia about a perpendicular axis passing through the center of the rod is given by,
`\mathbf{I_{O-O’} = \frac{M.L^{2}}{12} + \frac{1}{4}.m_{1}.L^{2} + \frac{1}{4}.m_{2}.L^{2}}`
Read below for more details about each of the conditions and how to derive them.
Moment of inertia for a Rod:
A] Moment of inertia about an axis passing through the center of rod:
The moment of inertia of the rod about the axis perpendicular to the rod and passing through the center (see axis O-O’ below figure) is given by,
`\mathbf{I = \frac{ML^{2}}{12}}`
Here are the steps to derive this equation:-
1] Value of dm:
Assume, the rod consists of a number of point masses. Consider a point mass ‘dm’ of length ‘dx’ is located at distance x from the central axis O-O’.
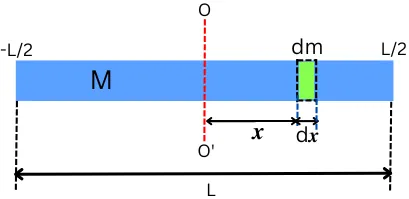
Assume the rod has uniform density over length. For the rod, linear mass density (λ) is given by,
`\lambda = \frac{\text{total mass of rod}}{\text{total length}} = \frac{M}{L}\cdots[1]`
Similarly, for the smaller element dm of length dx, the λ is given by,
`\lambda = \frac{dm}{dx}`
`dm = \lambda.dx`
Putting the value of `\lambda` from [1],
`dm = \frac{M}{L}.dx\cdots[2]`
2] Moment of inertia of mass dm about central axis O-O’:
The moment of inertia of a smaller point mass dm about axis O-O’ is given by,
`dI = x^{2}.dm`
`dI = x^{2}.\frac{M}{L}.dx`
3] Moment of inertia of the rod about central axis:
The moment of inertia of the complete rod about axis O-O’ can be calculated by integrating the dI over the complete length.
`I = \int dI = \int_{-\L/2}^{L/2} x^{2}.\frac{M}{L}.dx`
`I = \frac{M}{L}. \int_{-\L/2}^{L/2} x^{2}.dx`
`I = \frac{M}{L}.[\frac{x^{3}}{3}]_{-\L/2}^{L/2}`
`I = \frac{M}{L}. [\frac{L^{3}}{24}+\frac{L^{3}}{24}]`
`\mathbf{I = \frac{M.L^{2}}{12}}`
B] Moment of inertia of a rod about axis at the end:
For the thin rod of mass M and length L, the moment of inertia about the axis at its one of end and perpendicular to the rod (see C-C’ in below figure) is given by,
`\mathbf{I = \frac{M.L^{2}}{3}}`
Here are the steps to derive the above equation:-
1] Moment of inertia of dm:
Consider the thin rod consisting of a number of small masses ‘dm’ of thickness ‘dx’. Consider a single point mass dm located at the distance x from the axis C-C’.
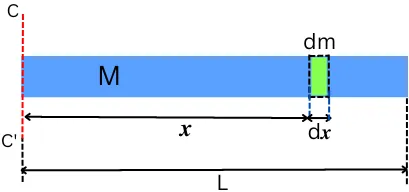
The moment of inertia of this small mass about the axis C-C’ is given by,
`dI = x^{2}.dm`
Put `dm = \frac{M}{L}.dx` from equation [2],
`dI = x^{2}.\frac{M}{L}.dx`
2] Moment of inertia of rod:
The moment of inertia of the whole rod about the axis at the end is calculated by integrating the dI over the complete length of the rod,
`I = \int_{0}^{L} x^{2}.\frac{M}{L}.dx`
`I = \frac{M}{L}\int_{0}^{L} x^{2}.dx`
`I = \frac{M}{L}[\frac{ x^{3}}{3}] _{0}^{L}`
`I = \frac{M}{L}[\frac{ L^{3}}{3}-0]`
`\mathbf{I = \frac{M.L^{2}}{3}}`
C] Moment of inertia of the rod about an axis parallel to the rod:
The below figure shows the thin rod of mass M away from the parallel axis O-O’ at a distance of x. In comparison with length, the thin rod has a smaller cross-section.
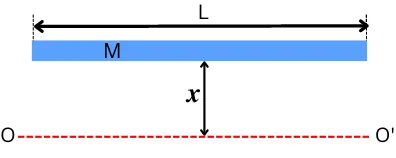
This parallel thin rod acts as a point mass for the axis O-O’ at a distance x.
Thus, in such case, the moment of inertia of a thin rod about a parallel axis is given by,
`\mathbf{I = M \times x^{2}}`
Moment of inertia of a rod with point mass at end:
In this case, the point masses are attached at the end of the rod. The point mass can be attached at the single or both ends.
Let’s discuss the moment of inertia in each of the conditions.
A] With point mass at one end:
The below figure shows the thin rod with one point mass attached at its single end. The axis C-C’ is at the end of the rod and axis O-O’ passes through the center of the rod.
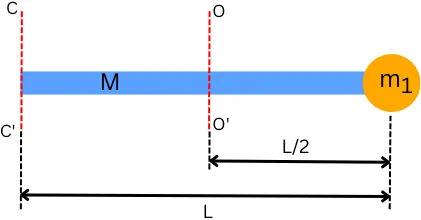
The moment of inertia about axis O-O’ of is given by,
`I_{O-O’}` = MOI of rod about O-O’ + MOI of point mass about O-O’
`I_{O-O’} = \frac{M.L^{2}}{12} + m_{1}\times\text{distance}^{2}`
`I_{O-O’} = \frac{M.L^{2}}{12} + m_{1}.(\frac{L}{2})^{2}`
`\mathbf{I_{O-O’} = \frac{M.L^{2}}{12} + \frac{m_{1}.L^{2}}{4}}`
The moment of inertia about axis C-C’ is given by,
`I_{C-C’}` = MOI of rod about C-C’ + MOI of point mass about C-C’
`I_{C-C’} = \frac{M.L^{2}}{3} + m_{1}\times\text{distance}^{2}`
`\mathbf{I_{C-C’} = \frac{M.L^{2}}{3} + m_{1}.L^{2}}`
B] With point mass at both ends:
Below figure shows the thin rod of mass M, with two point masses m1 and m2 attached on its both ends. Here the axis O-O’ passes through the center of the rod.
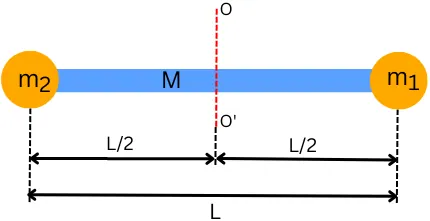
The moment of inertia of the above system about the axis O-O’ is given by,
`I_{O-O’}` = MOI of rod about O-O’ + MOI of m1 about O-O’ + MOI of m2 about O-O’
`I_{O-O’} = \frac{M.L^{2}}{12} + (m_{1}\times\text{distance}^{2}) + (m_{2}\times\text{distance}^{2})`
`I_{O-O’} = \frac{M.L^{2}}{12} + m_{1}.[L/2]^{2} + m_{2}.[L/2]^{2}`
`\mathbf{I_{O-O’} = \frac{M.L^{2}}{12} + \frac{1}{4}.m_{1}.L^{2} + \frac{1}{4}.m_{2}.L^{2}}`
If both point masses have the same mass (m1 = m2),
∴ `I_{O-O’} = \frac{M.L^{2}}{12} + \frac{1}{4}.m_{1}.L^{2} + \frac{1}{4}.m_{1}.L^{2}`
`I_{O-O’} = \frac{M.L^{2}}{12} + \frac{1}{2}.m_{1}.L^{2}`
Solved Numericals:
1] Find the moment of inertia of a rod of mass 2 kg and length 5 m about the axis passing through the center of the rod and the axis at the end of the rod.
Given:
M = 2 Kg
L = 5 m
Solution:
a] About the axis passing through the centroid:
The moment of inertia about the axis passing through the centroid of the thin rod is given by,
`I = \frac{M.L^{2}}{12}`
`I = \frac{2\times5^{2}}{12}`
I = 4.167 Kg.m2
b] About the axis passing through the end:
The moment of inertia about the axis passing through the end of the thin rod is given by,
`I = \frac{M.L^{2}}{3}`
`I = \frac{2\times5^{2}}{3}`
I = 16.67 Kg.m2
2] Consider a rod of mass 0.5 Kg and length of 1 m that has a point mass of 0.1 Kg attached at one of its ends. Find the moment of inertia of the complete system about the axis passing through another end.
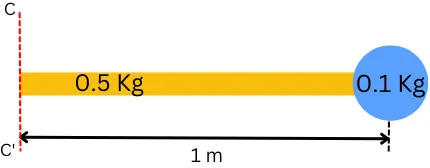
Given:
M = 0.5 Kg
L = 1 m
m1 = 0.1 Kg
Solution:
The moment of inertia of the rod with a point mass at one end about the axis at another end is given by,
`I_{C-C’} = \frac{M.L^{2}}{3} + m_{1}.L^{2}`
`I_{C-C’} = \frac{0.5\times1^{2}}{3} + 0.1\times1^{2}`
`\mathbf{I_{C-C’}}` = 0.266 Kg.m2
You may like to read: