What are symbols of polar moment of inertia and mass moment of inertia?

The polar moment of inertia is denoted by the symbol 'J' and the Mass moment of inertia is denoted by symbol ' 𝙸 '.

What are the units of polar moment of inertia and mass moment of inertia?

In the SI system, the units of polar moment of inertia and mass moment of inertia are m⁴ and Kg.m² respectively. In the FPS system, the units of polar moment of inertia and mass moment of inertia are ft⁴ and lb.ft² respectively.

Polar moment of inertia vs Mass moment of inertia difference

Polar moment of inertia vs Mass moment of inertia can be differentiated as the polar moment of inertia shows the resistance of the object to the torsional deformation and mass moment of inertia shows the resistance for the change in angular acceleration.

Contents:

Polar moment of inertia:

The polar moment of inertia is the ability of the cross-section of an object to resist the deformation caused by the torsional loading.

The polar moment of inertia is calculated about the axis perpendicular to the plane of cross-section and passing through the centroid of a cross-section.

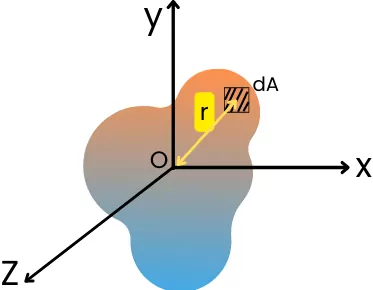
Polar moment of inertia vs Mass moment of inertia

For the cross-section shown in the above figure, the polar moment of inertia about the z-axis is given by,

J = ∫ r².dA

The polar moment of inertia is also given by the following formula,

J = 𝙸𝐱 + 𝙸𝐲

Where,
𝙸𝐱 = Moment of inertia of the given section about the x-axis
𝙸𝐲 = Moment of inertia about y-axis

Mass moment of inertia:

The mass moment of inertia is the resistance offered by the body to the change in angular acceleration. The mass moment of inertia depends on the mass of the object and its position from the rotating axis.

The mass moment of inertia shows the distribution of mass from the rotating axis.
The equation for the mass moment of inertia is as follows,

𝙸 = ∫ r².dm

The mass moment of inertia can be calculated by using the following equation,

𝙸 = `\sum M_{i}.r_{i}^{2}`

Where,
M = Mass of each object
r = Distance of mass from the axis of rotation

Polar moment of inertia vs mass moment of inertia:

Sr. No.	Polar moment of inertia	Mass moment of inertia
1]	The polar moment of inertia shows the resistance offered by the object against the torsional deformation.	The mass moment of inertia shows the resistance offered by the object to the change in angular acceleration.
2]	The polar moment of inertia depends on the area of cross-section of the object.	The mass moment of inertia depends on the mass of the object and its location from the axis of rotation.
3]	The polar moment of inertia shows the distribution of area from the reference axis.	The mass moment of inertia shows the distribution of mass from the axis of rotation.
4]	The equation of the polar moment of inertia is, J = ∫r².dA.	The equation for the mass moment of inertia is, 𝙸 = ∫r².dm.
5]	The polar moment of inertia has an SI unit of m⁴.	The SI unit for the mass moment of inertia is Kg.m².
6]	The dimensional formula for the polar moment of inertia is [L⁴M⁰T⁰].	The mass moment of inertia has a dimensional formula of [L²M¹T⁰].
7]	The polar moment of inertia is necessary for the design of rotating components like shafts, coupling, bolts, etc.	The mass moment of inertia is necessary for the design of components like flywheels of rotary machines, gears, fans, etc.

The above table shows the difference between mass moment of inertia and polar moment of inertia.

FAQs:

What are symbols of polar moment of inertia and mass moment of inertia?

The polar moment of inertia is denoted by the symbol ‘J’ and the Mass moment of inertia is denoted by symbol ‘𝙸‘.
What are the units of polar moment of inertia and mass moment of inertia?

In the SI system, the units of polar moment of inertia and mass moment of inertia are m⁴ and Kg.m² respectively.
In the FPS system, the units of polar moment of inertia and mass moment of inertia are ft⁴ and lb.ft² respectively.