Polar moment of inertia Explained: Formulae, Calculation, Examples

For the shaft or axle in torsion, the polar moment of inertia is significant in finding the torsional shear stress occurring on the shaft or to determine the angle of twist in a shaft.

So in this article, we are going to understand the polar moment of inertia, how to calculate it, its formulae for the different standard shapes, and also the solved numericals. So let’s start.

In this article, we’re going to discuss:

1. What is the Polar moment of inertia?
2. How to calculate the polar moment of inertia?
3. Polar moment of inertia formulae for different shapes:
   3.1. For solid circular shaft:
   3.2. For hollow circular shaft:
   3.3. For rectangular plate:
   3.4. For square:
4. Solved examples:
5. FAQS:

What is the Polar moment of inertia?

Polar moment of inertia is the ability of a shape of a cross-section of an object to resist a torsional deformation (caused by the torque along the axis perpendicular to the cross-section). It is also known as a moment of inertia about the axis perpendicular to the cross-section plane.

The high value of the polar moment of inertia indicates the cross-section has more ability to resist torsional deformation.

It is denoted by the symbol `\mathbf{I_{z}}` or J and has an SI unit of m⁴.

As per the perpendicular axis theorem, the polar moment of inertia at any point can be calculated by adding the moment of inertia about two mutually perpendicular axes that lie into the plane of the cross-section and are concurrent at the same point.

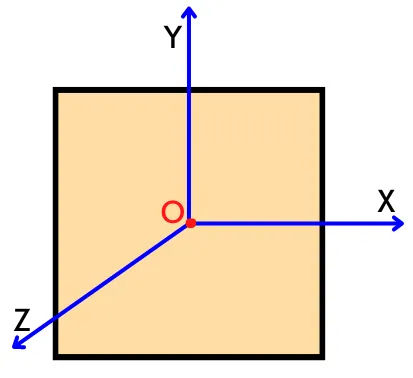
The above figure shows the plane lamina with two perpendicular axes (x & y) lying into the plane and the z-axis is perpendicular to the plane and all three axes (x, y, z) are concurrent at ‘O’.

Thus, by using the perpendicular axis theorem, the equation for the polar moment of inertia about the z-axis (Jₒ) is given by,

J_o​​ = 𝙸_z = 𝙸_x + 𝙸_y

Where
𝙸_x = Moment of inertia about the x-axis
𝙸_y = Moment of inertia about the y-axis

Therefore, by finding the moment of inertia about the x and y-axis and adding them together, we can find the polar moment of inertia.

To know about how the polar moment of inertia is different from the moment of inertia, read our this article.

How to calculate the polar moment of inertia?

The polar moment of inertia for the standard shapes can be found using direct formulas which we are going to see below. But in the case of irregular shapes, it is difficult to get a standard formula.

So in such cases, use the following steps to obtain a polar moment of inertia.

Step 1] Divide the complex shape into simple geometric shapes that have a standard formula for the moment of inertia:

In this step, we have to divide the complex shape/plane for which we have to calculate the polar moment of inertia into simple geometric shapes that have standard formulas for a moment of inertia like Square, Rectangle, Triangle, Circle, Semi circle.

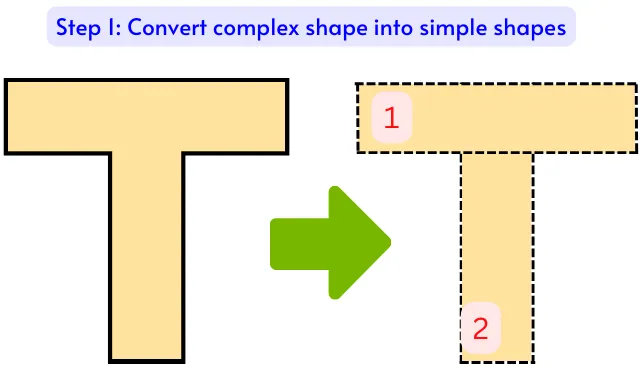
Step 2] Find the position of a centroid and area for each of the simple geometric shapes:

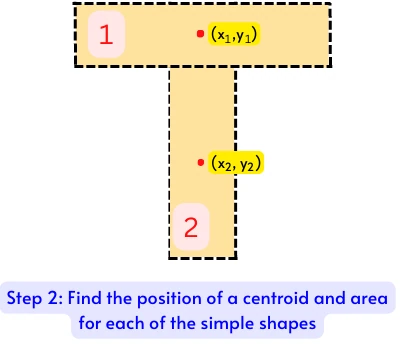
To find the Area (A_i) and Centroid position (x_i, y_i) for each standard shape, we have to use Area and centroid formulas for standard shapes.

Step 3] Find the Centroid position of the whole shape, and mark X_C and Y_C axis:

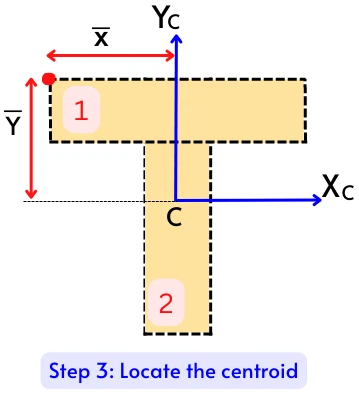
To find polar moment of inertia at the centroid, it is necessary to find the position of a centroid first. Use the formula below to calculate the position of the centroid.

`\bar{X}=\frac{\sum_{i=1}^{n} A_{i}.x_{i}}{A_{\text{total}}}`

`\bar{Y}=\frac{\sum_{i=1}^{n} A_{i}.y_{i}}{A_{\text{total}}`

Step 4] Find the area moment of inertia about the x and y axis (I_xc and I_yc) passing through the centroid of whole shape:

In this step, Find the moment of inertia of the whole shape about a centroidal axis (I_xc and I_yc), which is equal to the addition of the moment of inertia of each standard shape about the centroidal axis.

I_xc = I_1xc + I_2xc + – – – + I_nxc (For centroidal X-axis)

I_yc = I_1yc + I_2yc + – – – + I_nyc (For centroidal Y-axis)

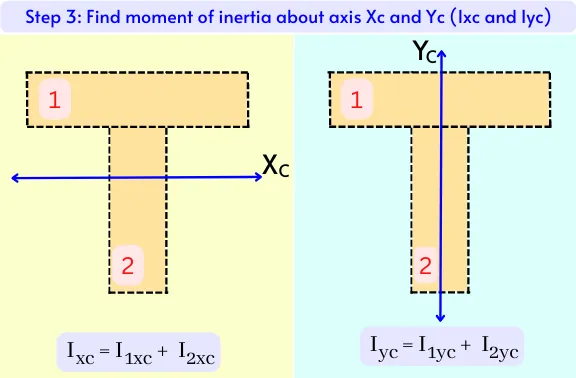
Use the parallel axis theorem for calculating the area moment of inertia of each standard shape (I_1xc, I_2xc– – -, I_nxc and I_1yc, I_2yc– – -, I_nyc) about the centroidal axis X_c and Y_c.

I_c = I + A.d²

Where, d = Distance between the centroid of the whole shape and the centroid of each standard shape

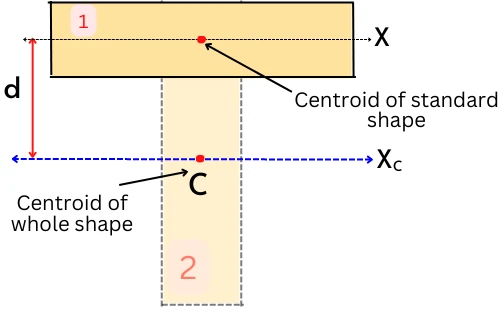
We have an article for finding the moment of inertia using the parallel axis theorem.

Step 5] Find the polar moment of inertia at the centroid using the below formula:

I_zc = I_xc + I_yc

See solved numerical below in this article to know these steps in a better way.

Polar moment of inertia formulae for different shapes:

Following are the equations for the standard shapes:

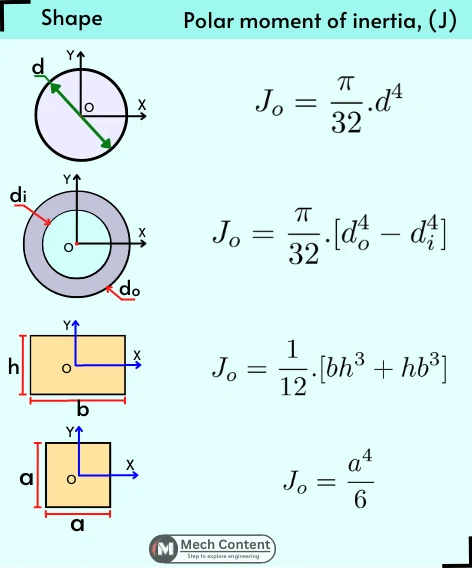
Read below to know how to derive above formulae,

1] For solid circular shaft:

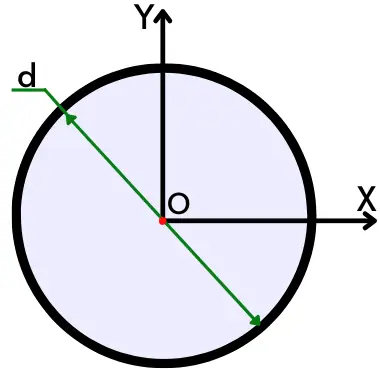
The moment of inertia of the circular profile about the centroidal x-axis is given by,

𝙸_x = `\frac{\pi }{64}` d⁴

The moment of inertia of the circular profile about the centroidal y-axis is given by,

𝙸_y = `\frac{\pi }{64}` d⁴

Thus the polar moment of inertia about ‘O’ is given by,

J_o = 𝙸_x + 𝙸_y

J_o = `\frac{\pi }{64}` d⁴ + `\frac{\pi }{64}` d⁴

J_o = `\mathbf{\frac{\pi }{32}}` d⁴

This is the equation for finding the polar moment of inertia for the circular shaft.

2] For hollow circular shaft:

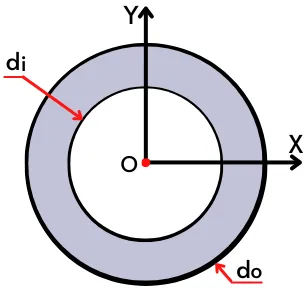
The above figure shows the cross-section profile of a hollow circular shaft with an outer diameter (do) and inner diameter (di).

The moment of inertia of the hollow circular shaft about the centroidal x-axis is given by,

𝙸_x = `\frac{\pi }{64}. (d_{o}^{4}-d_{i}^{4})`

The moment of inertia of the hollow circular shaft about the centroidal y-axis is given by,

𝙸_y = `\frac{\pi }{64}.(d_{o}^{4}-d_{i}^{4})`

Now the polar moment of inertia for the hollow circular shaft about point ‘O’ is given by,

Jₒ = 𝙸_x + 𝙸_y

Putting the values of 𝙸_x and 𝙸_y,

Jₒ = `[\frac{\pi }{64}. (d_{o}^{4} – d_{i}^{4})]+[\frac{\pi }{64}. (d_{o}^{4}-d_{i}^{4})]`

J_o = `\mathbf{\frac{\pi }{32}}.\mathbf{(d_{o}^{4}-d_{i}^{4})}`

This is the equation for finding a polar moment of inertia of hollow shafts, pipes, or tubes.

3] For rectangular plate:

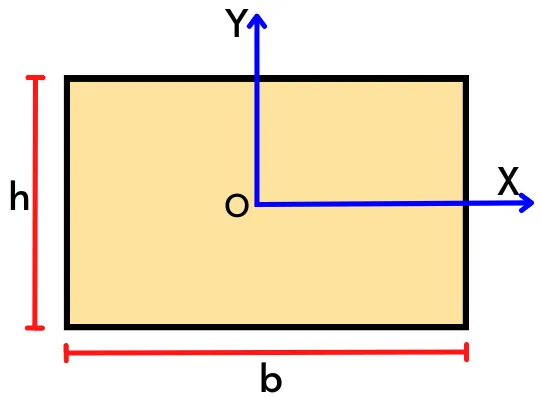
The above figure shows the profile of the thin rectangular plate with a width of ‘b’ and a height of ‘h’.

The moment of inertia of a rectangular shape about the centroidal x-axis is given by,

𝙸_x = `\frac{bh^{3}}{12}`

The moment of inertia of a rectangular shape about the centroidal y-axis is given by,

𝙸_y = `\frac{hb^{3}}{12}`

Now the polar moment of inertia for the rectangular shape is given by,

Jₒ = 𝙸_x + 𝙸_y

J_o = `\frac{bh^{3}}{12}+\frac{hb^{3}}{12}`

J_o = `\mathbf{\frac{1}{12}}` [bh³ + hb³]

This is the equation of the polar moment of inertia for a rectangular shape.

4] For square:

The square is a rectangle with all sides the same. Hence by putting b = d = a in the above equation of rectangle, we can get the formula for the polar moment of inertia of a square about the centroid.

J_o = `\frac{1}{12}.[a.a^{3}+a.a^{3}]`

J_o = `\mathbf{\frac{a^{4}}{6}}`

Solved examples:

1] The hollow circular pipe has an outer diameter of 40 mm and an inner diameter of 35 mm. Find the polar moment of inertia for the pipe.

Given:
dₒ = 40 mm
d_i= 35 mm

Solution:

Using the formula of the polar moment of inertia for a hollow circular cross-section,

J_o = `\frac{\pi }{32} \times [d_{o}^{4}-d_{i}^{4}]`

J_o = `\frac{\pi }{32}` [40⁴ – 35⁴]

Jo = 104003.89 mm⁴

---

2] Find polar moment of inertia about the axis passing through the centroid of the below T-section.

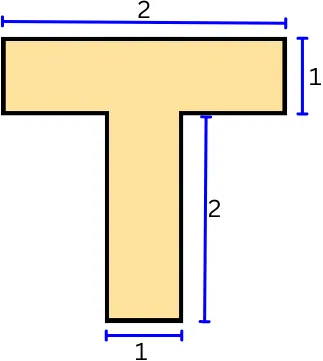
Solution:

Step 1, 2 and 3: Divide the T shape into simple shape and Find the position of centroid:

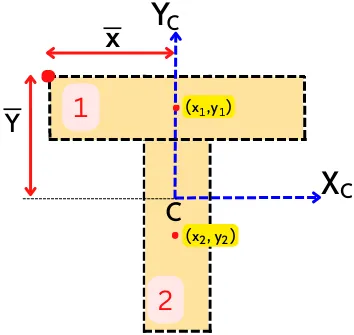
From the given diagram,
A₁ = 2 × 1 = 2, x₁ = 1, y₁ = 0.5
A₂ = 1 × 2 = 2, x₂ = 1, y₂ = 2

The position of the centroid is given by,

`\bar{Y}=\frac{A_{1}.y_{1}+A_{2}.y_{2}}{A_{1}+A_{2}}`

`\bar{Y}=\frac{2\times0.5+2\times2}{2+2}`

`\mathbf{\bar{Y}}` = 1.25

`\bar{X}=\frac{A_{1}.x_{1}+A_{2}.x_{2}}{A_{1}+A_{2}}`

`\bar{X}=\frac{2\times1+2\times1}{2+2}`

`\mathbf{\bar{X}}` = 1

Step 4: Moment of inertia about Xc and Yc:

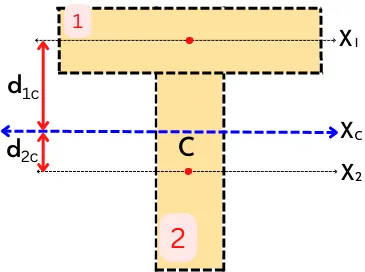
From the above figure,
d_1c = `\bar{Y}-y_{1}` = 0.75
d_2c = `y_{2}-\bar{Y}` = 0.75

The Moment of inertia about the centroidal axis, X_C axis is given by,

`I_{xc}=I_{1xc}+I_{2xc}`

Applying the parallel axis theorem,

`I_{xc}=[I_{1x}+A_{1}.d_{1c}^{2}]+[I_{2x}+A_{2}.d_{2c}^{2}]`

`I_{xc}=[(\frac{b.h^{3}}{12})_{1}+A_{1}.d_{1c}^{2}]+[(\frac{b.h^{3}}{12})_{2}+A_{2}.d_{2c}^{2}]`

`I_{xc}=[\frac{2\times1^{3}}{12}+2\times0.75^{2}]+[\frac{1\times2^{3}}{12}+2\times0.75^{2}]`

`\mathbf{I_{xc}}` = 3.083

The Moment of inertia about the centroidal axis, Y_C axis is given by,

`I_{yc}=I_{1yc}+I_{2yc}`

As axis Y_C, y₁, y₂ are same,

`I_{yc}=I_{1y}+I_{2y}`

`I_{yc}=[\frac{h.b^{3}}{12}]_{1}+[\frac{h.b^{3}}{12}]_{2}`

`I_{yc}=[\frac{1\times2^{3}}{12}]+[\frac{2\times1^{3}}{12}]`

`\mathbf{I_{yc}}` = 0.833

Step 5: Find the polar moment of inertia:

J_o = `I_{xc}+I_{yc}`

J_o = 3.083 + 0.833

J_o = 3.916

FAQs: