The parallel axis theorem is the method to find the moment of inertia of the object about any axis parallel to the axis passing through the centroid. This theorem is applicable for the mass moment of inertia and also for the area moment of inertia.
In this article, we’re going to discuss:
- What is the parallel axis theorem?
- Parallel axis theorem formula:
- Parallel axis theorem derivation:
- How to use the parallel axis theorem?
- Parallel axis theorem solved examples:
What is the parallel axis theorem?
Statement for the mass moment of inertia:-
“The mass moment of inertia about the axis parallel to the axis passing through the center of mass is given by the sum of mass moment of inertia about an axis passing through the center of mass (`I_{\text{COM}}`) and product of mass (M) and square of perpendicular distance between two axes (h)”.
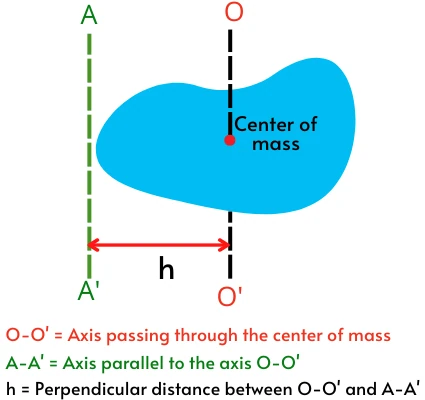
Mathematically, it can be expressed as,
`I = I_{\text{COM}} + Mh^{2}`
Statement for the Area moment of inertia (second moment of area):-
“The area moment of inertia about the axis parallel to the centroidal axis is given by the sum of an area moment of inertia about a centroidal axis (`I_{c}`) and product of area (A) and square of the perpendicular distance (h) between two axes.”
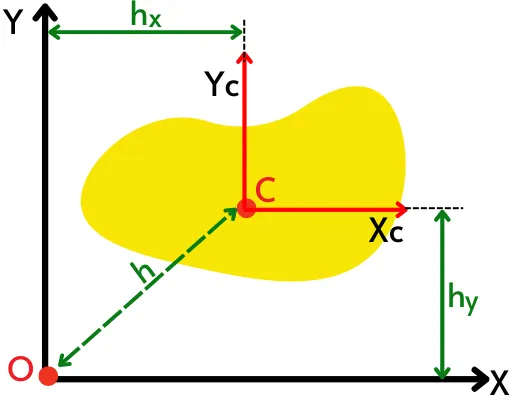
In the above figure, the X-axis is parallel to the centroidal axis `X_{c}` while the Y-axis is parallel to the centroidal axis `Y_{C}`.
For the plane lamina shown in the above figure the area moment of inertia about the x-axis is given by,
`I_{x} = I_{xc} + Ah_{y}^{2}`
Where `I_{xc}` = Second moment of area about centroidal axis `X_{c}`
And the area moment of inertia about the y-axis is given by,
`I_{y} = I_{yc} + Ah_{x}^{2}`
Where, `I_{yc}` = Second moment of area about centroidal axis `Y_{c}`
The theorem is also useful for finding the polar moment of inertia, therefore the polar moment of inertia about the origin ‘O’ is given by,
`I_{O} = I_{C} + Ah^{2}`
Where `I_{C}` = Polar moment of inertia at the centroid ‘C’
Parallel axis theorem formula:
In the case of the mass moment of inertia, the equation of the parallel axis theorem is as follows,
`I=I_{\text{COM}}+Mh^{2}`
Where,
`I_{\text{COM}}` = Mass moment of inertia about the axis passing through the center of mass
`I` = Mass moment of inertia about an axis parallel to the axis passing through the COM
h = Perpendicular distance between two axis
M = Mass of the object
In the case of the second moment of area, the equation of the parallel axis theorem is as follows,
`I=I_{C}+Ah^{2}`
Where,
`I_{C}` = Second moment of area (Area moment of inertia) about the axis passing through the centroid
`I` = Second moment of area (Area moment of inertia) about an axis parallel to the centroidal axis
h = Perpendicular distance between two axis
A = Area of the plane lamina
Parallel axis theorem derivation:
Following are the proofs of the parallel axis theorem for the mass moment of inertia and for the second moment of area.
1] Parallel axis theorem (Mass moment of inertia):-
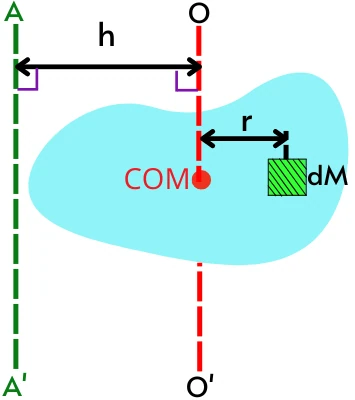
The axis O-O’ shown in the above figure passes through the center of mass (COM) of the object while the axis A-A’ (parallel to the axis O-O’) is located at a distance ‘h’ from the axis O-O’.
Consider a smaller portion of mass ‘dm’ located at a distance ‘r’ from the center of mass of the object.
The mass moment of inertia of the smaller mass ‘dm’ about the axis A-A’ is given by,
`dI = \text{distance}^{2}.dm`
`dI = (r+h)^{2}.dm`
`dI = (r^{2}+2rh+h^{2}).dm`
`dI = r^{2}.dm+2rh.dm+h^{2}.dm`
Integrate `dI` to find the total mass moment of inertia about axis A-A’.
`\intdI = \intr^{2}.dm+\int2rh.dm+\inth^{2}.dm`
`I = \intr^{2}.dm+2h\intr.dm+h^{2}\intdm`
As `\intr^{2}.dm = I_{COM}`, i.e. mass moment of inertia about an axis passing through the center of mass.
`\therefore I = I_{COM}+2h\intr.dm+h^{2}\intdm`
`I = I_{\text{COM}}+2h\intr.dm+h^{2}.M \cdots [\because \intdm = M\text{ i.e. mass of the object}]`
`I = I_{\text{COM}}+2hM\frac{\intr.dm}{M}+M.h^{2}`
The above term `\frac{\intr.dm}{M}` indicates the equation to find the position of the center of mass. But as shown in the above figure, the distance ‘r’ indicates the position of the mass ‘dM’ from the center of mass (COM) of the object.
Thus the equation `\frac{\intr.dm}{M}` indicates the distance of the center of mass from the center of mass itself. Therefore `\frac{\intr.dm}{M}` = 0.
`I = I_{\text{COM}}+0+M.h^{2}`
`I = I_{\text{COM}}+M.h^{2}`
This is the equation of the parallel axis theorem for the mass moment of inertia.
2] Parallel axis theorem (second moment of area):-
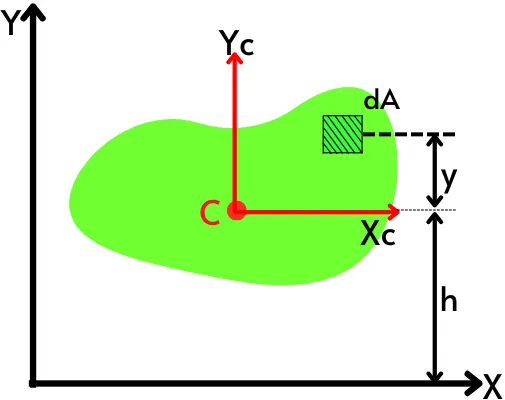
The centroid of the shape shown in the above figure is located at a distance ‘h’ from the x-axis and the axis Xc and Yc indicate the centroidal axis of the object.
Consider a smaller portion ‘dA’ located at distance ‘y’ from the centroidal axis Xc. The second moment of area of the portion dA about the X-axis is given by,
`dI_{x} = \text{Distance}^{2}.dA`
`dI_{x} = (y+h)^{2}.dA`
`dI_{x} = (y^{2}+2hy+h^{2}).dA`
`dI_{x} = y^{2}.dA+2hy.dA+h^{2}.dA`
Integrate the `dI_{x}` to find the second moment of area of the complete shape about the x-axis.
`\int dI_{x} = \inty^{2}.dA+\int2hy.dA+\inth^{2}.dA`
`I_{x} = \inty^{2}.dA+2h\inty.dA+h^{2}\intdA`
Where `\inty^{2}.dA = I_{xc}`, i.e. Moment of inertia (second moment of area) of whole shape about centroidal axis `X_{c}`
`\therefore I_{x} = I_{xc}+2h\inty.dA+h^{2}\intdA`
`I_{x} = I_{xc}+2h\inty.dA+h^{2}.A \cdots[\because\intdA=A \text{ i.e. total area of the shape}]`
The term `\inty.dA` indicates the equation for the first moment of area of the shape. But as shown in the above figure, the distance ‘y’ indicates the position of the area ‘dA’ from the centroid of the object.
Thus the term `\inty.dA` indicates the moment of area of the total shape about the centroid itself. As the first moment of inertia about the centroidal axis is zero, therefore the term `\inty.dA` is equivalent to zero.
`\therefore I_{x} = I_{xc}+0+A.h^{2}`
`\therefore I_{x} = I_{xc}+A.h^{2}`
This is the equation of the parallel axis theorem for the second moment of area.
How to use the parallel axis theorem?
Here are the steps for finding the mass moment of inertia by the parallel axis theorem:-
Step 1] Find a mass moment of inertia about the axis passing through the center of mass of the body by using standard formulae.
Step 2] Find the perpendicular distance (h) between the axis passing through the center of mass and the parallel axis.
Step 3] Use the parallel axis theorem equation to find a mass moment of inertia about the parallel axis.
Here are the steps for finding the area moment of inertia (second moment of area) by the parallel axis theorem:-
Step 1] Find a moment of inertia about the centroid of the shape by using standard formulae.
Step 2] Find the area of the shape (A) and the perpendicular distance (h) between the two parallel axes.
Step 3] Use the parallel axis theorem equation to find a moment of inertia of the shape about the parallel axis.
Parallel axis theorem solved examples:
Solving numerical is the best way to clear the concepts, therefore we have provided a few numerical based on the parallel axis theorem that will help you to understand the theorem.
1] For the given cross-section, calculate the moment of inertia about the x and y-axis.
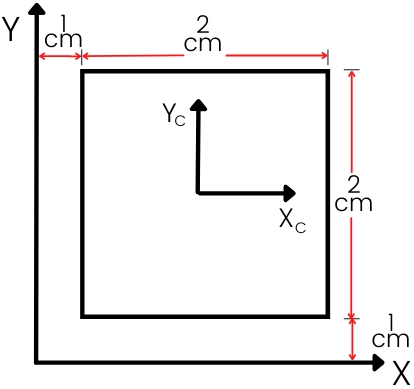
Solution:-
A) Moment of inertia about the x-axis:-
Step 1] Calculate the moment of inertia about the centroidal x-axis:-
For the square section, the moment of inertia about the centroidal x-axis is given by,
`I_{XC}=\frac{bd^{3}}{12}=\frac{2\times 2^{3}}{12}`
`I_{XC}=1.33\ \text{cm}^{4}`
Step 2] Area (A) and perpendicular distance (h):-
Area = 2 × 2 = 4 cm²
Distance between centroidal axis (`X_{c}`) and x-axis,
`h_{y}=1+\frac{2}{2}=2\ \text{cm}`
Step 3] Moment of inertia about the x-axis:-
By the parallel axis theorem,
`I_{X}=I_{XC}+Ah_{y}^{2}`
`I_{X}=1.33+(4\times 2^{2})`
`\therefore \text{Moment of inertia about the x-axis}, I_{X}=17.33\ \text{cm}^{4}`
B) Moment of inertia about the y-axis:-
Step 1] Calculate the moment of inertia about the centroidal y-axis:-
For the square section, the moment of inertia about the centroidal y-axis is given by,
`I_{YC}=\frac{bd^{3}}{12}=\frac{2\times 2^{3}}{12}`
`I_{YC}=1.33\ \text{cm}^{4}`
Step 2] Area (A) and perpendicular distance (h):-
Area = 2 × 2 = 4 cm⁴
Distance between centroidal axis (`Y_{c}`) and y-axis,
`h_{x}=1+\frac{2}{2}=2\ \text{cm}`
Step 3] Moment of inertia about the y-axis:-
By the parallel axis theorem,
`I_{Y}=I_{YC}+Ah_{x}^{2}`
`I_{Y}=1.33+(4\times 2^{2})`
`\therefore \text{Moment of inertia about the y-axis}, I_{Y}=17.33\ \text{cm}^{4}`
2] The sphere of mass 5 Kg has a radius of 80 mm. Find the moment of inertia of the sphere about the axis tangent to the sphere.
Given:
M = 5 Kg
R = 80 mm = 0.08 m
Solution:-
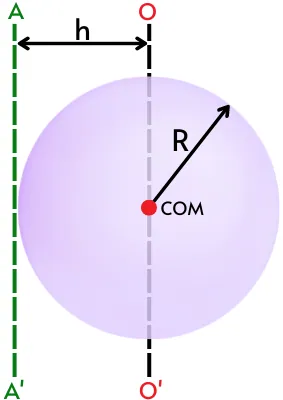
The moment of inertia of the sphere about the axis passing through the center of mass is given by,
`I_{\text{COM}} = \frac{2}{5}MR^{2}`
`I_{\text{COM}} = \frac{2}{5} \times 5 \times 0.08^{2}`
`I_{\text{COM}}` = 0.0128 Kg.m²
The perpendicular distance between the axis O-O’ and axis A-A’ is given by,
h = R = 0.08 m
Now by using the parallel axis theorem, the moment of inertia about the tangent is given by,
`I = I_{\text{COM}}+Mh^{2}`
`I = 0.0128 + (5 \times 0.08^{2})`
`I = 0.0448\ \text{Kg.m}^{2}`
FAQs:
-
When can you apply the parallel axis theorem?
Here are the conditions for the use of the parallel axis theorem:-
1] Both axes should be parallel to each other.
2] One of the axes should pass through the centroid of the body. -
Is the parallel axis theorem and Huygens–Steiner theorem similar?
Yes, the parallel axis theorem is also known as Huygens–Steiner theorem.
-
Can we use the parallel axis theorem for the polar moment of inertia?
Yes, the parallel axis theorem is also applicable to the polar moment of inertia.
-
Can we use the parallel axis theorem for the object with non-uniform mass distribution?
Yes, it is also valid for objects with non-uniform mass distribution.
People also look for: