What is Perpendicular axis theorem of moment of inertia?
The perpendicular axis theorem states that “The moment of inertia about the axis perpendicular to the two coplanar axes is given by the sum of the moment of inertia about this two coplanar axis.”
For the object shown in the figure, the X and y axes are coplanar and perpendicular to each other and the z-axis is perpendicular to both X-axis and Y-axis. If all the axis are concurrent, then the moment of inertia about the z-axis is given by,
`I_{z}` = `I_{x}` + `I_{y}`
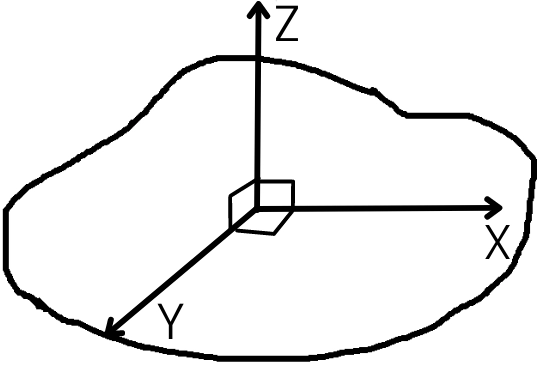
Where,
`I_{x}` = Moment of inertia about x-axis
`I_{y}` = Moment of inertia about y-axis
`I_{z}` = Moment of inertia about z-axis
In this article, we’re going to discuss:
- When to use perpendicular axis theorem?
- How to use the perpendicular axis theorem?
- Perpendicular axis theorem proof:
When to use perpendicular axis theorem?
Here are the conditions to use the perpendicular axis theorem:-
1) The two axes x and y should be on the same plane.
2) X and Y-axis should be perpendicular.
3) Z-axis should be perpendicular to both axis and perpendicular to the plane of the body.
How to use the perpendicular axis theorem?
Here are the steps for finding a moment of inertia by using the perpendicular axis theorem:-
Step 1] Check the condition for the applicability of the perpendicular axis theorem.
Step 2] Find the moment of inertia about the coplanar axis `I_{x}` and ‘I_{y}`.
Step 3] Find the moment of inertia about the Z-axis by using the perpendicular axis theorem equation.
Perpendicular axis theorem proof:
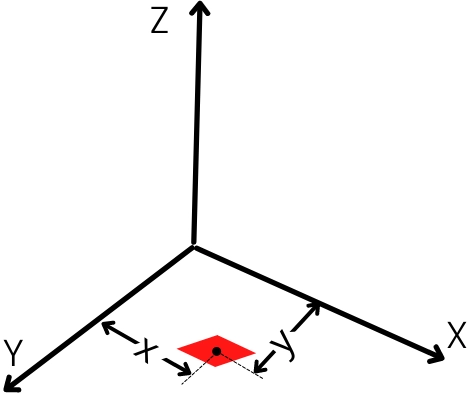
Consider an elemental mass dm in XY plane with centroid is placed at distance x and y from X-axis and Y-axis respectively.
The moment of inertia of mass about x-axis:-
`dI_{x} = d_{m}.y^{2}`————-(1)
The moment of inertia of mass about the y-axis is,
`dI_{y} = d_{m}.x^{2}` ————-(2)
The moment of inertia about the z-axis is given by,
`dI_{z} = d_{m}.z^{2}` ————-(3)
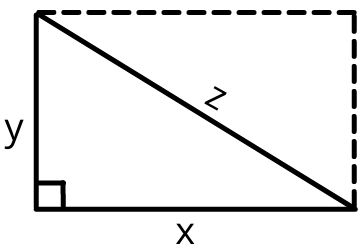
But from figure, we can conclude that,
`z^{2}=y^{2}+x^{2}`
Put `z^{2}` value in the equation 3.
`\therefore dI_{z}=d_{m}(y^{2}+x^{2})`
`dI_{z}=d_{m}y^{2}+d_{m}x^{2}`
By considering equation 1 and 2, the equation of `dI_{z}` will become,
`dI_{z} = dI_{x} + dI_{y}`
By integrating both sides of the equation, we get
`I_{z} = I_{x} + I_{y}`
This is the required equation for the perpendicular axis theorem.
Read also: