Torsional shear stress refers to the internal resistance of a material against twisting loads. Understanding torsional shear stress is crucial in engineering, especially for designing shafts, as it helps determine how materials withstand twisting forces.
Here you can about its calculation and application in both solid and hollow shafts.
In this article, we’re going to discuss:
- What is Torsional shear stress?
- Torsional Shear Stress Equation:
2.1. Torsional shear stress formula for circular shaft:
2.2. Maximum torsional shear stress for circular shaft: - Torsional shear stress solved examples:
What is Torsional shear stress?
Torsional shear stress is the shear stress offered by the body against torsional load or twisting load. it is denoted by the symbol ‘𝜏’.
The value of torsional shear stress varies within the cross-section of the object. The value for shear stress is minimum at the neutral axis of the cross-section while it is maximum at the outermost surface of the cross-section of the object.
The units of torsional shear stress are N/m² in the SI system while lb/ft² in the FPS system.
Torsional Shear Stress Equation:
Torsional shear stress can be found by using the torsional equation.
Therefore,
`\tau= \frac{T}{J}\times r`
Where,
T = Applied torque
J = Polar moment of inertia
r = Distance between the neutral axis and the point where shear stress is to be calculated
Torsional shear stress formula for circular shaft:
A] For solid shaft:
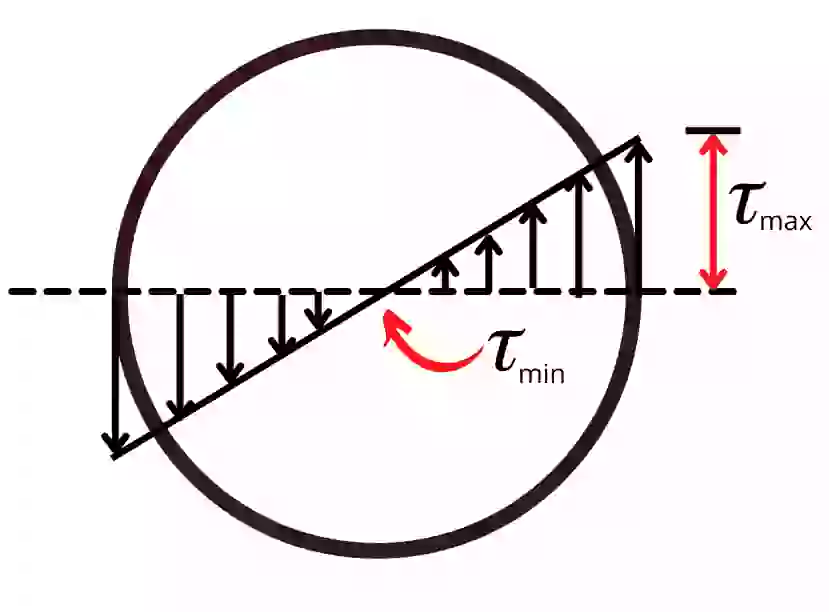
The above diagram shows the torsional shear stress distribution in a hollow circular shaft. In that figure, the value for 𝜏 is minimum at the neutral axis while it is maximum at r = d/2
For the solid circular shaft, the shear stress at any point in the shaft is given by,
`\tau= \frac{T}{J}\times r`
But for solid shaft,
`J= \frac{\pi }{32}\times d^{4}`
Therefore the torsional shear stress for the circular shaft is given by,
`\tau= \frac{32T}{\pi\times d^{4} }\times r`
B] For hollow shaft:
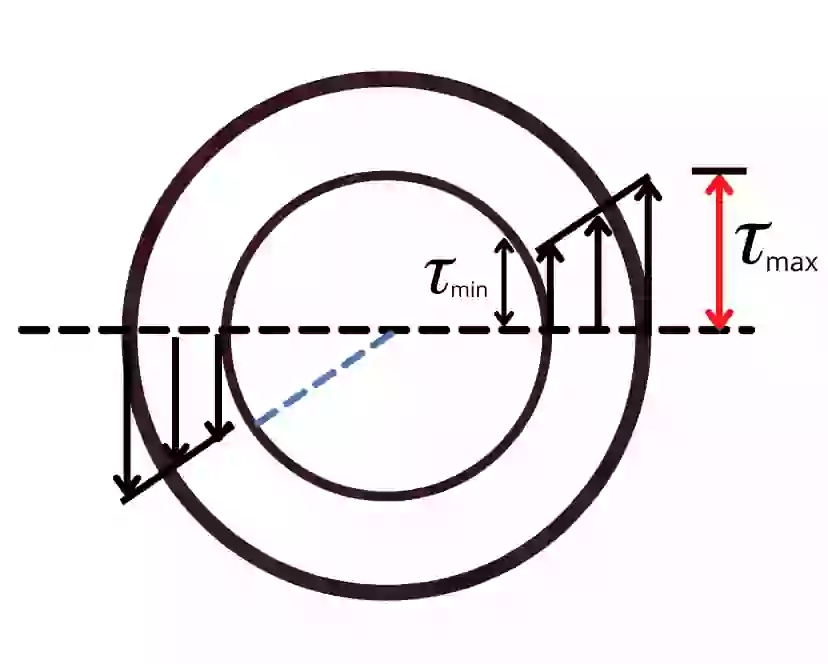
The above diagram shows the torsional shear stress distribution in a hollow circular shaft. In that figure, the value for 𝜏 is minimum at r = di/2 while it is maximum at r = do/2
For hollow circular shaft with outer diameter (do) and inner diameter (di), the polar moment of inertia is given by,
`J= (\frac{\pi }{32})\times [do^{4}-di^{4}]`
Therefore the torsional shear stress for hollow shaft is given by,
`\tau= \frac{32T}{\pi\times (do^{4}-di^{4}) }\times r`
Maximum torsional shear stress for circular shaft:
A] For solid shaft:
The maximum shear stress in a solid circular shaft is observed at the outermost surface where r = d/2
`\tau_{max}= \frac{32T}{\pi\times d^{4} }\times \frac{d}{2}`
`\tau_{max}= \frac{16T}{\pi\times d^{3} }`
B] For hollow shaft:
The maximum shear stress in a hollow circular shaft is observed at the outer diameter (do).
∴ r = do/2
`\tau_{max}= \frac{32T}{\pi\times (do^{4}-di^{4}) }\times\frac{do}{2}`
`\tau_{max}= \frac{16T\times do}{\pi\times (do^{4}-di^{4}) }`
Torsional shear stress solved examples:
1] The shaft of the motor is rotating with a maximum torque of 6 N.m. If the shaft has a diameter of 25 mm, find the maximum shear stress acting onto the shaft.
Given:
T = 3 N.m
d = 25 mm = 0.025 m
Solution:
The maximum shear stress acting on the solid circular shaft is given by,
`\tau_{\text{max}} = \frac{16T}{\pid^{3}}`
`\tau_{\text{max}} = \frac{16\times3}{\pi \times 0.025^{3}}`
`\therefore \tau_{\text{max}}= 977847.97\ \text{N/m}^²`
2] The hollow circular shaft shown in the below figure is under the torque of 5 N.m. Find the shear stress at the radius of r = 20 mm.
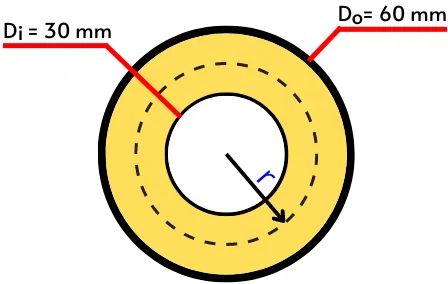
Given:
T = 5 N.m
`d_{i}` = 30 mm = 0.03 m
`d_{o}` = 60 mm = 0.06 m
r = 20 mm = 0.02 m
Solution:-
For the above hollow shaft, the polar moment of inertia is given by,
`J = \frac{\pi}{32}(d_{o}^{4} – d_{i}^{4})`
`J = \frac{\pi}{32}(0.06^{4} – 0.03^{4})`
`J = 1.192\times10^{-6} m^{4}`
The shear stress at r = 0.02 m is given by,
`\tau_{r=0.02m} = \frac{T}{J}\times r`
`\tau_{r=0.02m} = \frac{5}{1.192\times10^{-6}}\times 0.02`
`\therefore \tau_{r=0.02m}= 83892.61\ \text{N/m}^²`
Thanks for very nice information for newly learners with simple examples…