The study of principal strain helps in determining the object’s maximum value of normal strain and serves as a criterion for the maximum principal strain theory. Thus in this article, we will discuss this topic in detail.
Contents:
What is a Principal strain?
The principal strains are the maximum and minimum values of the normal strain experienced by an object. It acts on the principal planes where the value of shear strain is zero.
The principal planes are planes in an object that experience maximum/ minimum normal strain on the object and zero shear strains. Principal strain is denoted by the symbol `\varepsilon_{P}`.
In the case of plane stress conditions (a biaxial stress condition), the object has two principal strains (`\varepsilon_{P1}` & `\varepsilon_{P2}`). See below diagram.
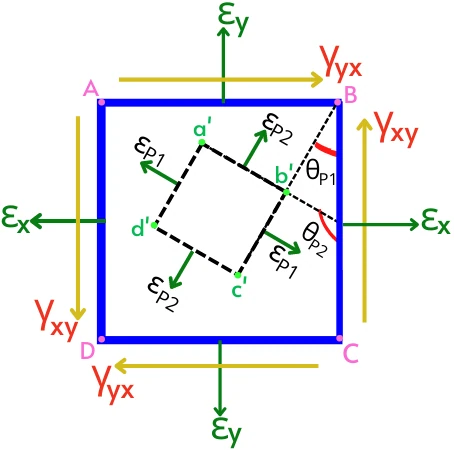
The object ABCD in the above figure is subjected to the normal strains (`\varepsilon_{x}` and `\varepsilon_{y}`) and shear strains (`\gamma_{xy}` and `\gamma_{yx}`).
While a’b’c’d’ indicates the principal planes in the object and the normal strain acting on these planes (`\varepsilon_{P1}` and `\varepsilon_{P2}`) indicates the principal strains.
The `\theta_{P1}` and `\theta_{P2}` indicate the orientation of the principal planes with respect to the reference plane ‘BC’.
Equation:
The equation to calculate the maximum (major) principal strain (`\varepsilon_{1}`) is as follows,
`\varepsilon_{1}=\frac{\varepsilon_{x}+\varepsilon_{y}}{2}+\sqrt{(\frac{\varepsilon_{x}-\varepsilon_{y}}{2})^{2}+(\frac{\gamma_{xy}}{2})^{2}}`
Where, `\varepsilon_{x},\varepsilon_{y}` = Normal strain in x and y direction respectively
`\gamma_{xy}` = Shear strain
The equation for the minimum (minor) principal strain (`\varepsilon_{2}`) is as follows,
`\varepsilon_{2}=\frac{\varepsilon_{x}+\varepsilon_{y}}{2}-\sqrt{(\frac{\varepsilon_{x}-\varepsilon_{y}}{2})^{2}+(\frac{\gamma_{xy}}{2})^{2}}`
The position of the plane (θP) for maximum principal strain is as follows,
`\theta_{P}=\frac{1}{2}tan^{-1}(\frac{\gamma_{xy}}{\varepsilon_{x}-\varepsilon_{y}})`
Explaination:
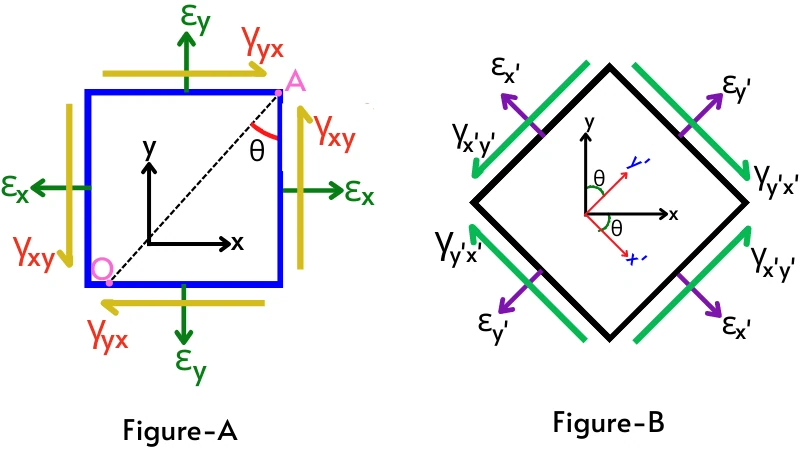
Above figure-A shows an element subjected to the normal and shear strains. While figure-B is the planes in the object (shown in figure-A) inclined at angle θ.
As shown in the above figure-B, the `\varepsilon_{x’}`, `\varepsilon_{y’}` are normal stresses and `\gamma_{x’y’}`, `\gamma_{y’x’}` are shear strain acting on the oblique planes.
The normal strain and shear strain acting on these planes is given by the strain transformation equations.
The normal and shear strain on this oblique plane is given by,
`\varepsilon_{x’}=(\frac{\varepsilon_{x}+\varepsilon_{y}}{2})+(\frac{\varepsilon_{x}-\varepsilon_{y}}{2})cos2\theta+(\frac{\gamma_{xy}}{2})sin2\theta`
`\varepsilon_{y’}=(\frac{\varepsilon_{x}+\varepsilon_{y}}{2})-(\frac{\varepsilon_{x}-\varepsilon_{y}}{2})cos2\theta-(\frac{\gamma_{xy}}{2})sin2\theta`
`\gamma_{x’y’}=-(\frac{\varepsilon_{x}-\varepsilon_{y}}{2})sin2\theta+(\frac{\gamma_{xy}}{2})cos2\theta`
The object contains numerous oblique planes oriented at different values of `\theta` from the reference plane. And each oblique plane in the element experiences a specific amount of normal strain and shear strain.
Among these different oblique planes, there are certain oblique planes present in the element that experiences zero shear strain (`\gamma` = 0). While the normal strains acting on these planes are known as the Principal strains (`\varepsilon_{P}`).
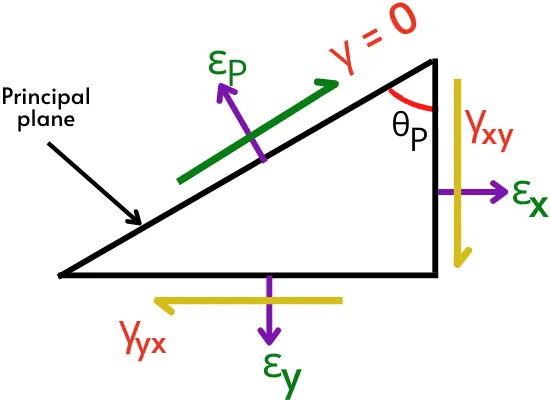
In the plane stress condition, there are two planes oriented at an angle `\theta_{P1}` and `\theta_{P2}` from the reference plane.
The higher value of the normal strain acting on one of these planes is known as the Major principal strain while the smaller value of the normal strain is known as the Minor principal strain.
The major principal strain is given by,
`\varepsilon_{1}=\frac{\varepsilon_{x}+\varepsilon_{y}}{2}+\sqrt{(\frac{\varepsilon_{x}-\varepsilon_{y}}{2})^{2}+(\frac{\gamma_{xy}}{2})^{2}}`
The minor principal strain is given by,
`\varepsilon_{2}=\frac{\varepsilon_{x}+\varepsilon_{y}}{2}-\sqrt{(\frac{\varepsilon_{x}-\varepsilon_{y}}{2})^{2}+(\frac{\gamma_{xy}}{2})^{2}}`
The location of the plane of maximum principal strain is given by,
`\theta_{P}=\frac{1}{2}tan^{-1}(\frac{\gamma_{xy}}{\varepsilon_{x}-\varepsilon_{y}})`
The planes of maximum (major) and minimum (minor) principal strain are generally mutually perpendicular to each other.
i.e. `\theta_{P2}=\theta_{P1}+90^{\circ}`
Principal strain solved examples:
1] For the object shown in the below diagram, find the major and minor principal strain and the location of the principal planes.
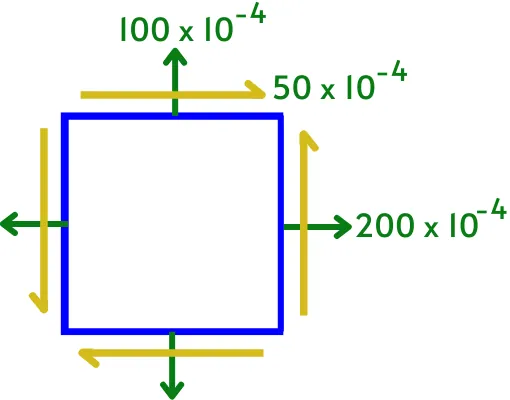
Solution:-
The normal strain and the shear strain in the above figure are as follows,
`\varepsilon_{x}=200\times10^{-4}=0.02`
`\varepsilon_{y}=100\times10^{-4}=0.01`
`\gamma_{xy}=50\times10^{-4}=0.005`
1] Principal strain:
The major principal strain is given by,
`\varepsilon_{P1}=\frac{\varepsilon_{x}+\varepsilon_{y}}{2}+\sqrt{(\frac{\varepsilon_{x}-\varepsilon_{y}}{2})^{2}+(\frac{\gamma_{xy}}{2})^{2}}`
By putting all the values in the above equation, we get
`\mathbf{\varepsilon_{P1}=0.0205}`
Minor principal strain is given by,
`\varepsilon_{P2}=\frac{\varepsilon_{x}+\varepsilon_{y}}{2}-\sqrt{(\frac{\varepsilon_{x}-\varepsilon_{y}}{2})^{2}+(\frac{\gamma_{xy}}{2})^{2}}`
By putting all the values in the above equation, we get
`\mathbf{\varepsilon_{P2}=9.409\times10^{-3}}`
2] Location of the planes of principal strain:
The location of the plane of maximum principal strain is given by,
`\theta_{P1}=\theta_{P}=\frac{1}{2}tan^{-1}(\frac{\gamma_{xy}}{\varepsilon_{x}-\varepsilon_{y}})`
`\theta_{P1}=\frac{1}{2}tan^{-1}(\frac{0.005}{0.02-0.01})`
`\theta_{P1}=13.28^{\circ}`
The location of the plane of minimum principal strain is given by,
`\theta_{P2}=\theta_{P1}+90^{\circ}`
`\theta_{P2}=13.28^{\circ}+90^{\circ}=103.28^{\circ}`
`\mathbf{\therefore\theta_{P1}=13.28^{\circ}, \theta_{P2}=103.28^{\circ}}`
FAQs:
-
Why are principal strains significant?
The principal strain gives the maximum and minimum normal strain and its location in the object. It is used in ‘Saint Venant theory of failure’ which is used for the safe design of the machine parts.
-
What is the relation between the planes of major and minor principal strain?
The plane of major principal strain (θ🇵₁) and the plane of minor principal strain (θ🇵₂) are mutually perpendicular to each other.
∴ θ🇵₂ = θ🇵₁ + 90° -
What is the maximum number of principal strains that can exist in a biaxial stress situation?
In a situation of biaxial stress, there can only be two principal strains.
You may like this: