For the safe design of the component, it is necessary to know about the maximum stresses acting inside the component and its location.
The principal stress gives the maximum normal stress acting inside the component and its position. In this article, we will go through comprehensive information on principal stress.

In this article, we’re going to discuss:
- What is Principal stress?
1.1. Principal stress explanation: - What is Maximum and Minimum principal stress?
2.1. How to calculate Maximum and Minimum principal stress? - Von mises stress vs Principal stress:
- Sign convention:
- Principal stress example:
What is Principal stress?
Principal stress is the normal stress acting onto the principal plane that has zero shear stress.
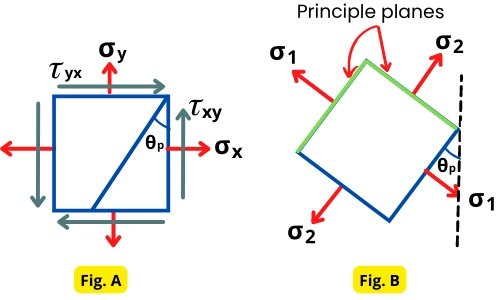
The above figure. A show the member subjected to the axial stresses as well as shear stresses and figure-B shows the principal stresses and principal planes.
What is principal plane?
A principal plane is an oblique plane in an object that bears no shear stress. The principal planes lie at angle `\theta_{p}`, (also called principal angle) from the reference plane as shown in figure-B. There is no shear stress acts on these planes.
Here’s what principal stress means:
The normal stresses acting on that plane (`\sigma_{1}` and `\sigma_{2}`) are the principal stresses.
Principal stress explanation:
Let’s break down this concept in more simple way.
Oblique Planes and Stresses acting on it:
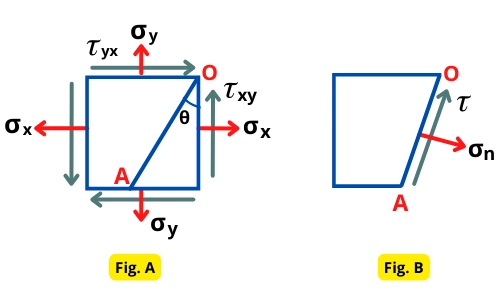
The member shown in the figure. A is subjected to the axial stresses in the x and y direction (`\sigma_{x}, \sigma_{y}`) and complementary shear stresses on horizontal and vertical planes (`\tau_{xy}, \tau_{yx}`).
Oblique Planes: Other than horizontal and vertical planes, the member also has numerous inclined planes that are inclined at different angles θ (0° to 90°) from the reference plane. These planes are known as oblique planes.
As shown in the above figure. B, the oblique plane OA (inclined at at angle θ) experiences the following two types of stresses:
A] Normal stress (σₙ): The stress perpendicular to the oblique plane is the normal stress (`\sigma_{n}`).
The normal stress on an oblique plane inclined at angle θ is given by,
`\sigma_{n}=(\frac{\sigma_{x}+\sigma_{y}}{2})+(\frac{\sigma_{x}-\sigma_{y}}{2})cos2\theta + \tau_{xy}sin2\theta`
b] Shear stress (𝜏): The stress acting parallel to the plane is the shear stress on an oblique plane. It is given by,
`\tau=(\frac{\sigma_{x}-\sigma_{y}}{2})sin2\theta-\tau_{xy} cos2\theta`
Principal Plane and Principal Stress:
Now let’s understand what is principal plane and principal stress.
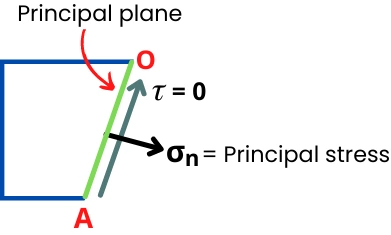
Principal planes: It is such oblique planes that experiences zero shear stress. For the components subjected to biaxial stresses, there are two planes on which the value of shear stress is zero.
Formula for position of principal Plane (From reference axis):
`\theta_{P}=\frac{1}{2}tan^{-1}.(\frac{2\tau_{xy}}{\sigma_{x}-\sigma_{y}})`
How this formula derived:
To find a position of this principal plane (θ𝗽) from the reference plane, put `\tau` = 0 in the equation of `\tau`.
`0=(\frac{\sigma_{x}-\sigma_{y}}{2})sin2\theta_{P}-\tau_{xy} cos2\theta_{P}`
`(\frac{\sigma_{x}-\sigma_{y}}{2})sin2\theta_{P}=\tau_{xy} cos2\theta_{P}`
`\frac{sin2\theta_{P}}{cos2\theta_{P}}=\frac{2\tau_{xy}}{\sigma_{x}-\sigma_{y}}`
`tan2\theta_{P}=\frac{2\tau_{xy}}{\sigma_{x}-\sigma_{y}}`
`\therefore \theta_{P}=\frac{1}{2}tan^{-1}.(\frac{2\tau_{xy}}{\sigma_{x}-\sigma_{y}})`
This is the position of the principal plane from the reference plane.
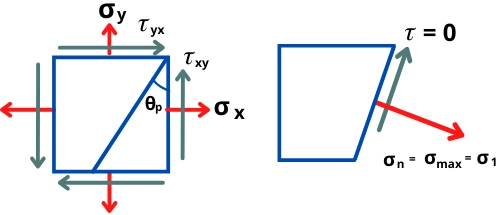
Principal stress: The normal stress acts onto the principal plane is known as the principal stress.
For biaxial (2D) stress conditions, there are two principal stresses known as Major principal stress and minor principal stress.
What is Maximum and Minimum principal stress?
For the member subjected to the biaxial stresses, the two principal stresses are as follows:
Maximum principal stress:
Maximum principal stress or major principal stress is the maximum value of normal stress acting on one of the principal planes where the value of shear stress is zero.
The value of maximum principal stress is given by,
`\sigma_{1}=(\frac{\sigma_{x}+\sigma_{y}}{2})+\sqrt{(\frac{\sigma_{x}-\sigma_{y}}{2})^{2}-\tau_{xy}^{2}}`
Minimum principal stress:
Minimum or minor principal stress is the minimum value of principal stress acting on one of the principal planes where the value of shear stress is zero.
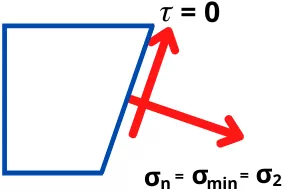
The value of minimum principal stress is given by,
`\sigma_{2}=(\frac{\sigma_{x}+\sigma_{y}}{2})-\sqrt{(\frac{\sigma_{x}-\sigma_{y}}{2})^{2}-\tau_{xy}^{2}}`
How to calculate Maximum and Minimum principal stress?
If the values of the axial stresses (`\sigma_{x} and \sigma_{y}`) and complementary shear stresses (`\tau_{xy} or \tau_{yx}`) are known, then the maximum and minimum principal stress can be calculated by the following methods:
1] Analytical method:
In the analytical method, the principal stresses can be calculated by using the following formulae,
`\sigma_{\text{max}}=\sigma_{1} = (\frac{\sigma_{x}+\sigma_{y}}{2})+\sqrt{(\frac{\sigma_{x}-\sigma_{y}}{2})^{2}+\tau_{xy}^{2}}`
`\sigma_{\text{min}} = \sigma_{2}=(\frac{\sigma_{x}+\sigma_{y}}{2})-\sqrt{(\frac{\sigma_{x}-\sigma_{y}}{2})^{2}+\tau_{xy}^{2}}`
2] Graphical method (Mohr’s circle):
The mohr’s circle is another and easy method to find the stresses on each oblique plane and principal stresses.
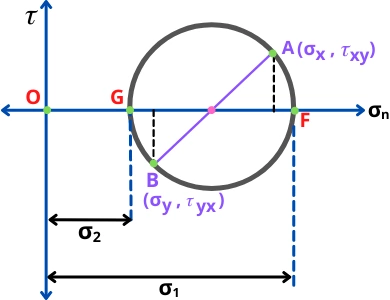
From above Mohr’s circle,
`\sigma_{\text{max}}=\sigma_{1}=\text{Distance OF}`
`\sigma_{\text{min}}=\sigma_{2}=\text{Distance OG}`
Von mises stress vs Principal stress:
| Sr. No. | Von mises stress | Principal stress |
|---|---|---|
| 1] | The von mises stress is the equivalent stress calculated from the distortion energy. | Principal stress is the real stress acting onto the oblique plane that has zero shear stress. |
| 2] | Von mises stress is used in the von-mises theory of failure. | It is used in the maximum principal stress theory of failure. |
| 3] | The von mises stress is suitable for the design of ductile materials. | The principal stress is suitable for the design of brittle materials. |
Sign convention:
Following is the sign convention used for the principal stress:
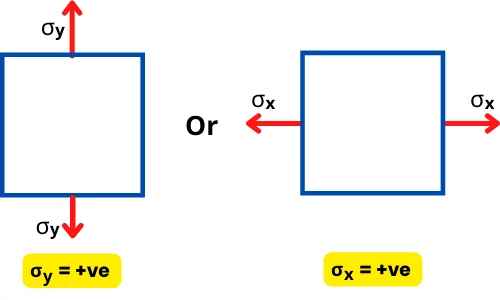
1] Axial stress:
The tensile axial stress is considered positive.
The compressive axial stress is considered negative.
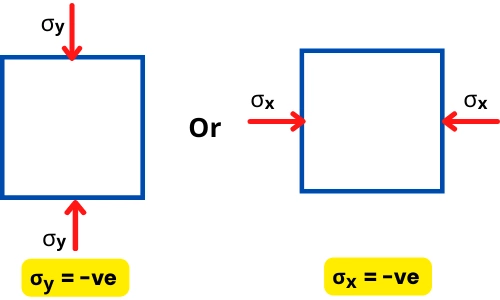
2] Complementary shear stress:
- Shear stress on the vertical plane (shown by red arrows) is in a clockwise sense: Positive
- Shear stresses on the vertical plane (shown by red arrows) are in an anticlockwise sense: Negative
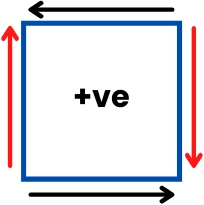
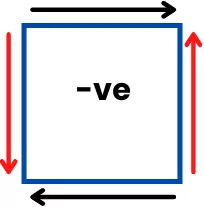
Principal stress example:
1] The state of stress on members is shown below, find the maximum and minimum amount of principal stress.
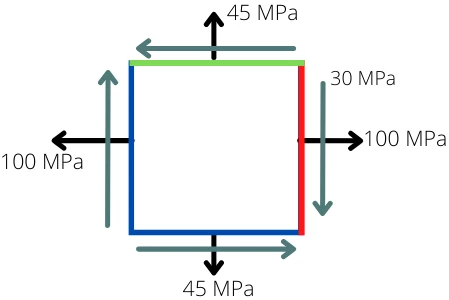
Given:
`\sigma_{x}` = 100 Mpa
`\sigma_{y}` = 45 Mpa
`\tau_{\text{xy}}` = 30 Mpa
Solution:
The maximum principal stress on the member is given by,
`\sigma_{1} = (\frac{\sigma_{x}+\sigma_{y}}{2}) + \sqrt{(\frac{\sigma_{x}-\sigma_{y}}{2})^{2}+\tau_{xy}^{2}}`
`\sigma_{1} = (\frac{100+45}{2}) + \sqrt{(\frac{100-45}{2})^{2}+30^{2}}`
`\mathbf{\sigma_{1}}` = 113.197 Mpa
The minimum principal stress on a member is given by,
`\sigma_{1} = (\frac{\sigma_{x}+\sigma_{y}}{2}) – \sqrt{(\frac{\sigma_{x}-\sigma_{y}}{2})^{2}+\tau_{xy}^{2}}`
`\sigma_{1} = (\frac{100+45}{2}) – \sqrt{(\frac{100-45}{2})^{2}+30^{2}}`
`\mathbf{\sigma_{2}}` = 31.802 Mpa
2] Find the stresses acting on the principal planes for the below stress condition.
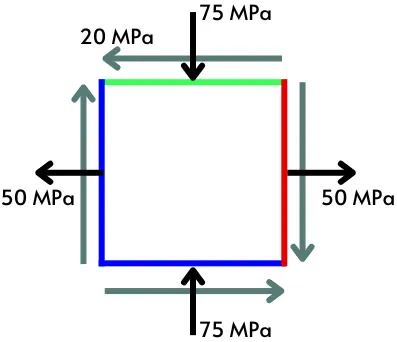
Given:
`\sigma_{x}` = 50 Mpa
`\sigma_{y}` = -75 Mpa
`\tau_{xy}` = 20 Mpa
Solution:
The stresses acting on the plane is a principal plane is given by,
`\sigma_{1}=\frac{\sigma_{x}+\sigma_{y}}{2}+ \sqrt{(\frac{\sigma_{x}-\sigma_{y}}{2})^{2}+\tau_{xy}^{2}}`
`\sigma_{1}=\frac{50+(-75)}{2}+\sqrt{(\frac{50-(-75)}{2})^{2} +20^{2}}`
`\sigma_{1}` = 53.122 MPa
`\sigma_{2}=\frac{\sigma_{x}+\sigma_{y}}{2}-\sqrt{(\frac{\sigma_{x}-\sigma_{y}}{2})^{2}+\tau_{xy}^{2}}`
`\sigma_{2}=\frac{\sigma_{x}+\sigma_{y}}{2}-\sqrt{(\frac{\sigma_{x}-\sigma_{y}}{2})^{2}+\tau_{xy}^{2}}`
`\sigma_{2}` = -78.122 MPa
Thus the principal stresses for the above biaxial stress condition are,
`\sigma_{1}=\text{53.122 MPa}`
`\sigma_{2}=\text{-78.122 MPa}`
FAQs:
-
What mean by the 1st principal stress?
The principal stress that has the maximum value is known as the first principal stress.
-
How do you find principal stresses and directions?
The value of the principal stresses and their directions can be found by using analytical formulae or by using Mohr’s circle.
-
Can maximum principal stress have a negative value?
The maximum principal stress can be positive or negative which is decided on the basis of the direction of the stress. If the principal stress is compressive then it is considered negative and if it is tensile then it is considered positive.
Related differences and article: