The von mises stress theory for failure also known as the maximum distortion energy theory which is developed by M.T. Huber and R.Von mises.
This article discusses von-mises theory in detail including its derivation, diagrams, calculation steps, and numerical.
Contents:
What is von mises stress theory?
Von mises theory states that the component subjected to the actual loading (Biaxial or triaxial) undergoes failure when the maximum distortion energy per unit volume in the object reaches to the yielding distortion energy per unit volume.
It means that the material will fail when `U_{d}` ≥ `U_{dy}`, Therefore to avoid failure, there must be, `U_{d}` < `U_{dy}`
Where,
`U_{d}` = Distortion energy in an object.
`U_{dy}` = Distortion energy value at yielding.
In the actual situation, when the object is subjected to axial stresses, it results in the change in volume of the object as well as a change in the shape of the object (distortion).
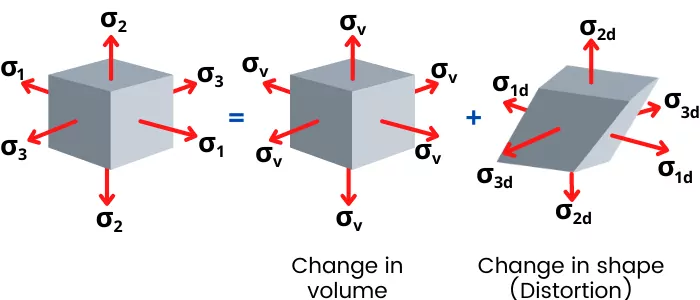
The change in the shape of the object without changing the volume is known as distortion.
The total strain energy in the object is also gets divided as strain energy to cause a change in volume and the strain energy to cause distortion (Distortion energy).
∴`U_{Total}` = `U_{V}+U_{d}`
Where,
`U_{\text{Total}}` = Total strain energy
`U_{V}` = Strain energy to cause a volume change
`U_{d}` = Strain energy to cause distortion
The engineering materials have the ability to absorb a larger amount of strain energy for volume change (`U_{V}`), But it isn’t able to absorb high distortion energy. Therefore these materials are more susceptible to distortion energy (Ud).
So in this theory, the failure in the material is decided on the basis of distortion energy.
Von mises stress formula:
The von mises stress formulas for the triaxial and biaxial loading are as follows:
1] For triaxial loading:
For the triaxial loading, the von mises stress is given by,
`\sigma=\sqrt{\sigma_{1}^{2}+\sigma_{2}^{2}+\sigma_{3}^{2}-\sigma_{1}\sigma_{2}-\sigma_{2}\sigma_{3}-\sigma_{3}\sigma_{1}}`
OR
`\sigma=\sqrt{\frac{(\sigma_{1}-\sigma_{2})^{2}+(\sigma_{2}-\sigma_{3})^{2}+(\sigma_{3}-\sigma_{1})^{2}}{2}}`
And to avoid the failure,
`\sqrt{\frac{(\sigma_{1}-\sigma_{2})^{2}+(\sigma_{2}-\sigma_{3})^{2}+(\sigma_{3}-\sigma_{1})^{2}}{2}}` < `\sigma_{yt}`
Where, `\sigma_{1}, \sigma_{2}, \sigma_{3}` are the principal stresses
2] For biaxial loading:
For biaxial loading, `\sigma_{3}` = 0, therefore von mises stress is given by,
`\sigma` = `\sqrt{\sigma_{1}^{2}+\sigma_{2}^{2}-\sigma_{1}\sigma_{2}}`
And to avoid failure,
`\sqrt{\sigma_{1}^{2}+\sigma_{2}^{2}-\sigma_{1}\sigma_{2}}` < `\sigma_{yt}`
Von mises stress derivation:
The actual loading can cause change in volume of the object as well as change in shape of the object (As shown in below figure).
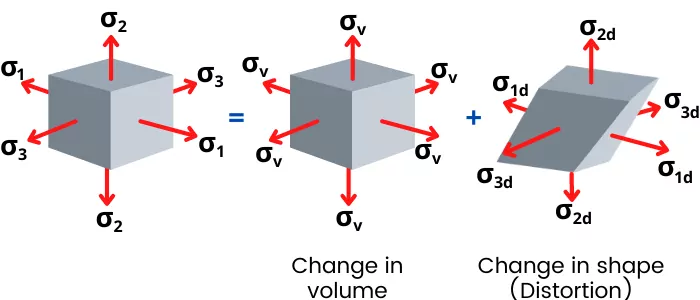
Therefore, the stress applied is also divide as follows,
`\sigma_{1}` = `\sigma_{1d}+\sigma_{v}`
`\sigma_{2}` = `\sigma_{2d}+\sigma_{v}`
`\sigma_{3}` = `\sigma_{3d}+\sigma_{v}`
The failure criteria for the von mises theory are based on the distortion energy in the object.
Following are the three steps for finding von mises stress failure criteria:
Step: 1] Finding distortion energy (`U_{d}`):
In actual loading, the total strain energy can be divided as follows,
`U_{\text{Total}}` = `U_{d}+U_{V}`
It is not possible to find the distortion energy, therefore, we can find it as follows,
`U_{d}` = `U_{\text{Total}}-U_{V}` –Equation [1]
Now we have to find the value of `U_{\text{total}}` and `U_{V}` to get the distortion energy `U_{d}`.
Step- 1A] Total strain energy (UTotal):
The strain energy for the uniaxial loading is given by,
`U` = `\frac{1}{2}\sigma.\varepsilon `
The total strain energy for triaxial load is given by,
`U_{\text{Total}} =U_{1}+U_{2}+U_{3}`
`U_{\text{Total}} = \frac{1}{2}\sigma_{1}\varepsilon_{1}+\frac{1}{2}\sigma_{2}\varepsilon_{2}+\frac{1}{2}\sigma_{3}\varepsilon_{3}`
The strain (ε) in each direction is given by,
`\varepsilon_{1} = \frac{\sigma_{1}}{E}-\nu \frac{\sigma_{2}}{E}-\nu \frac{\sigma_{3}}{E}`
`\varepsilon_{2} = \frac{\sigma_{2}}{E}-\nu \frac{\sigma_{1}}{E}-\nu \frac{\sigma_{3}}{E}`
`\varepsilon_{3} = \frac{\sigma_{3}}{E}-\nu \frac{\sigma_{1}}{E}-\nu \frac{\sigma_{2}}{E}`
Put this values of strains in equation of `U_{\text{Total}}`.
`U_{\text{Total}} = \frac{1}{2}\sigma_{1}[\frac{\sigma_{1}}{\E}-\nu \frac{\sigma_{2}}{E}-\nu \frac{\sigma_{3}}{E}]+\frac{1}{2}\sigma_{2}[\frac{\sigma_{2}}{E}-\nu \frac{\sigma_{1}}{E}-\nu \frac{\sigma_{3}}{E}]+\frac{1}{2}\sigma_{3}[\frac{\sigma_{3}}{E}-\nu \frac{\sigma_{1}}{E}-\nu \frac{\sigma_{2}}{E}]`
`U_{\text{Total}} = \frac{1}{2E}[\sigma_{1}^{2}+\sigma_{2}^{2}+\sigma_{3}^{2}-2\nu (\sigma_{1}\sigma_{2}+\sigma_{2}\sigma_{3}+\sigma_{3}\sigma_{1})]`
This is the value of total strain energy (`\mathbf{U_{\text{Total}}}`)
To find the `U_{V}`, it is necessary to find the value of `\sigma_{v}`
Step-1B] Value of `\sigma_{v}`:
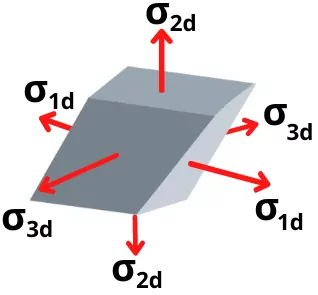
The strain arise due to the distortion energy is given by,
`\varepsilon_{vd} = \varepsilon_{1d}+\varepsilon_{2d}+\varepsilon_{3d}`
Strain in each uniaxial load is given by,
`\varepsilon_{1d} = \frac{\sigma_{1d}}{E}-\nu \frac{\sigma_{2d}}{E}-\nu \frac{\sigma_{3d}}{E}`
`\varepsilon_{2d} = \frac{\sigma_{2d}}{E}-\nu \frac{\sigma_{1d}}{E}-\nu \frac{\sigma_{3d}}{E}`
`\varepsilon_{3d} = \frac{\sigma_{3d}}{E}-\nu \frac{\sigma_{1d}}{E}-\nu \frac{\sigma_{2d}}{E}`
By putting values of `\varepsilon_{1d}`, `\varepsilon_{2d}` and `\varepsilon_{3d}` in equation of `\varepsilon_{vd}`, we get,
`\varepsilon_{vd} = (\frac{\sigma_{1d}}{E}-\nu \frac{\sigma_{2d}}{E}-\nu \frac{\sigma_{3d}}{E})+(\frac{\sigma_{2d}}{E}-\nu \frac{\sigma_{1d}}{E}-\nu \frac{\sigma_{3d}}{E})+(\frac{\sigma_{3d}}{E}-\nu \frac{\sigma_{1d}}{E}-\nu \frac{\sigma_{2d}}{E})`
`\varepsilon_{vd}=\frac{\sigma_{1d}+\sigma_{2d}+\sigma_{3d}}{E}.(1-2\nu)`
For the distortion, the change in volume is zero. Therefore volumetric strain `\varepsilon_{vd}` = 0.
`\varepsilon_{vd}= (\frac{\sigma_{1d}+\sigma_{2d}+\sigma_{3d}}{E}).(1-2\nu)=0`
Therefore in this case,
`(\frac{\sigma_{1d}+\sigma_{2d}+\sigma_{3d}}{E})`= 0 OR `(1-2\nu)` = 0
But `(1-2\nu)` = 0 s not possible. Because, `(1-2\nu)` = 0 for `\nu` = 0.5
The Poisson’s ratio, `\nu` = 0.5 is not possible for engineering materials.
Therefore (`1-2\nu`) ≠ 0.
Hence we can say that another term can be equls to zero,
`\frac{\sigma_{1d}+\sigma_{2d}+\sigma_{3d}}{E}` = 0 –Equation [2]
But `\sigma_{1d}=\sigma_{1}-\sigma_{v}`, `\sigma_{2d}=\sigma_{2}-\sigma_{v}` and `\sigma_{3d}=\sigma_{3}-\sigma_{v}`
∴ Put these values in equation [2]
`\frac{(\sigma_{1}-\sigma_{v})+(\sigma_{2}-\sigma_{v})+(\sigma_{3}-\sigma_{v})}{E}` = 0
`\frac{\sigma_{1}+\sigma_{2}+\sigma_{3}-3\sigma_{v}}{E}` = 0
∴ `\sigma_{v}` = `\frac{\sigma_{1}+\sigma_{2}+\sigma_{3}}{3}` — Equation[3]
This is the value of `\mathbf{\sigma_{v}}`.
Step-1C] Strain energy for volume change (`\mathbf{U_{V}}`):
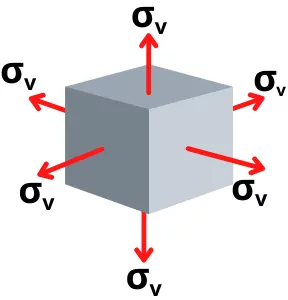
For the same stress `\sigma_{v}` in all direction, the total strain is given by,
`\varepsilon_{v}=\frac{3\sigma_{v}}{E}.(1-2\nu)`
The strain energy for volume change is given by,
`U_{V}=\frac{1}{2}\sigma_{v}\varepsilon_{v}`
Put value of `\varepsilon_{v}` in above equation of `U_{V}`
`U_{V}=\frac{1}{2}\sigma_{v}[\frac{3\sigma_{v}}{E}(1-2\nu)]`
`U_{V}=\frac{3\sigma_{v}^{2}}{2E}(1-2\nu)`
Put value of `\sigma_{v}` from Equation-[3]
`U_{V}=\frac{3}{2E}.(\frac{\sigma_{1}+\sigma_{2}+\sigma_{3}}{3})^{2}.(1-2\nu)`
`U_{V}=\frac{(\sigma_{1}+\sigma_{2}+\sigma_{3})^{2}}{6E}.(1-2\nu)`
`U_{V} = \frac{1-2\nu}{6E}.[\sigma_{1}^{2}+\sigma_{2}^{2}+\sigma_{3}^{2}+2\sigma_{1}\sigma_{2}+2\sigma_{2}\sigma_{3}+2\sigma_{3}\sigma_{1}]`
This is the value of `\mathbf{U_{V}}`
Step-1D] Distortion energy (`\mathbf{U_{d}}`):
Now put the value of `U_{\text{Total}}` and `U_{V}` in equation [1] to find `U_{d}`.
`U_{d}` = `U_{\text{Total}}-U_{V}`
`U_{d} = (\frac{1}{2E}.[\sigma_{1}^{2}+\sigma_{2}^{2}+\sigma_{3}^{2}-2\nu(\sigma_{1}\sigma_{2}+\sigma_{2}\sigma_{3}+\sigma_{3}\sigma_{1})]) – (\frac{1-2\nu}{6E}.[\sigma_{1}^{2}+\sigma_{2}^{2}+\sigma_{3}^{2}+2\sigma_{1}\sigma_{2}+2\sigma_{2}\sigma_{3}+2\sigma_{3}\sigma_{1}])`
By simplifying this calculation,
`U_{d} = \frac{1+\nu}{3E}.[\sigma_{1}^{2}+\sigma_{2}^{2}+\sigma_{3}^{2}-\sigma_{1}\sigma_{2}-\sigma_{2}\sigma_{3}-\sigma_{3}\sigma_{1}]` — Equation [4]
This is the equation of the distortion energy `\mathbf{U_{d}}`.
Step: 2] Distortion energy for yielding (`\mathbf{U_{dy}}`):
To find the distortion energy for yielding, put `\sigma_{1}` = `\sigma_{y}` and `\sigma_{2}` = 0, `\sigma_{3}` = 0 in equation [4] of `U_{d}`,
∴ `U_{dy}` = `\frac{1+\nu}{3E}[\sigma_{y}^{2}]` —Equation[5]
Step 3] Apply the theory of von mises stress to predict failure criteria:
As per von mises stress theory,
`U_{d}` < `U_{dy}`
Put values of `U_{d}` and `U_{dy}` in above relation from equation [4] and Equation [5]
`\frac{1+\nu}{3E}.[\sigma_{1}^{2}+\sigma_{2}^{2}+\sigma_{3}^{2}-\sigma_{1}\sigma_{2}-\sigma_{2}\sigma_{3}-\sigma_{3}\sigma_{1}]<\frac{1+\nu}{3E}.\sigma_{y}^{2}`
`[\sigma_{1}^{2}+\sigma_{2}^{2}+\sigma_{3}^{2}-\sigma_{1}\sigma_{2}-\sigma_{2}\sigma_{3}-\sigma_{3}\sigma_{1}] < \sigma_{y}^{2}`
`\mathbf{\sqrt{\sigma_{1}^{2}+\sigma_{2}^{2}+\sigma_{3}^{2}-\sigma_{1}\sigma_{2}-\sigma_{2}\sigma_{3}-\sigma_{3}\sigma_{1}}}<\mathbf{\sigma_{y}}`
This is the required failure criteria as per the von mises stress theory.
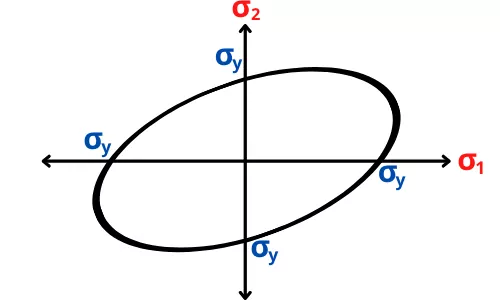
Von mises stress diagram (Region of safety):
To plot region of safety for the biaxial von mises stress, put `\sigma_{3}` = 0 in the equation of triaxial von mises stress.
The equation becomes,
`\sqrt{\sigma_{1}^{2}+\sigma_{2}^{2}-\sigma_{1}\sigma_{2}}` = `\sigma_{y}`
`\sigma_{1}^{2}+\sigma_{2}^{2}-\sigma_{1}\sigma_{2}` = `\sigma_{y}^{2}`
`(\frac{\sigma_{1}}{\sigma_{y}})^{2}+(\frac{\sigma_{2}}{\sigma_{y}})^{2}-(\frac{\sigma_{1}}{\sigma_{y}})(\frac{\sigma_{2}}{\sigma_{y}})` = 1
This equation is similar to the equation of ellipse (`x^{2}` + `y^{2}` – xy = 1).
Now the co-ordinates for the yielding diagram can be find as,
For `\mathbf{\sigma_{2}}` = 0
`\sqrt{\sigma_{1}^{2}+0+0}` = `\sigma_{y}`
`\sigma_{1}` = + `\sigma_{y}` OR `\sigma_{1}` = – `\sigma _{y}`
For `\mathbf{\sigma_{1}}` = 0
`\sqrt{0+\sigma_{2}^{2}+0}` = `\sigma_{y}`
`\sigma_{2}` = + `\sigma_{y}` OR – `\sigma _{y}`
Therefore as per the above co-ordinates, the region of safety becomes,
How to find von mises stress:
Following are the steps to calculate the von mises stress:
Step 1: Find the normal stresses and shear stresses.
Step 2: Find the principle stress `\sigma_{1}`, `\sigma_{2}` and `\sigma_{3}`
Step 3: Find the von mises stress using the formula,
`\sigma = \sqrt{\sigma_{1}^{2}+\sigma_{2}^{2}+\sigma_{3}^{2}-\sigma_{1}\sigma_{2}-\sigma_{2}\sigma_{3}-\sigma_{3}\sigma_{1}}`
Von mises stress example:
A cylindrical shaft with yield strength of 700 N/mm² is subjected to the bending stress of 140 N/mm² and torsional shear stress of 110 N/mm². Find the factor of safety based on von mises stress theory.
Given:
`S_{y}` = 700/mm²
`\sigma_{b}` = 140 N/mm²
`\tau` = 110 N/mm²
Solution:
Yield strength is given by,
`\sigma_{y}` = `\frac{S_{y}}{\text{FOS}}`
Maximum and minimum principal stress `\sigma_{1}` and `\sigma_{2}` are given by,
`\sigma_{1} = \frac{\sigma_{b}}{2}+\sqrt{(\frac{\sigma_{b}}{2})^{2}+\tau^{2}}`
`\sigma_{1}=\frac{140}{2}+\sqrt{(\frac{140}{2})^{2}+(110)^{2}}`
`\sigma_{1}` = 200.38 N/mm2
`\sigma_{2}=\frac{\sigma_{b}}{2}-\sqrt{(\frac{\sigma_{b}}{2})^{2}+\tau^{2}}`
`\sigma_{2}=\frac{140}{2}-\sqrt{(\frac{140}{2})^{2}+(110)^{2}}`
`\sigma_{2}` = – 60.38 N/mm2
By von mises stress theory, for biaxial stress condition,
`\sqrt{\sigma_{1}^{2}+\sigma_{1}^{2}-\sigma_{1}\sigma_{2}} = \sigma_{y}`
Put values of `\sigma_{1}`,`\sigma_{2}` and `\sigma_{y}`
`\sqrt{(200.38)^{2}+(-60.38)^{2}-(200.38)(-60.38)}=\frac{S_{yt}}{\text{FOS}}`
By putting `S_{yt}` = 700 N/mm², the FOS becomes,
236.425 = `\frac{700}{\text{FOS}}`
FOS = 2.96
Therefore, the Factor of safety based on von mises stress theory is 2.96.
FAQ’s
-
What is Von mises stress?
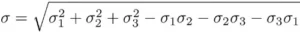
The von mises stress is the working stress as per the maximum von mises stress theory. It is given by the following formula.
Read also: