Maximum shear stress theory: Definition, Formula, with Pdf

Maximum shear stress theory (Tresca theory) is one of the theories of failure used for the safe design of mechanical components made up of a ductile material. The method is not suitable for hydrostatic stress conditions.

In this article, we’re going to discuss:

• What is Maximum shear stress theory?
• Maximum shear stress theory in three-dimensional loading:
• Maximum shear stress theory for biaxial loading:
• Yield surface for Maximum shear stress theory in biaxial loading:
• Maximum shear stress theory formula in form of axial stresses (`\sigma_{x}` and `\sigma_{y}`):
• Solved Numerical:
• FAQs:

What is Maximum shear stress theory?

Maximum shear stress theory states that when the maximum shear stress in an object reaches or exceeds the magnitude of yield shear stress in uniaxial loading, the object material undergoes failure.

In this theory of failure, the max shear stress developed in an object is a deciding factor for failure.

This theory is also known as the Tresca theory, named after French engineer, Henri Tresca.

Let me explain this theory simply.

Consider an object subjected to biaxial or triaxial loading. Due to the application of load, the object’s material experiences different normal stresses and shear stresses.

Among all stresses, for this failure theory, we are interested in the maximum value shear stress developed in an object.

While the yield shear stress in uniaxial loading `\tau_{\text{y. uniaxial}}` is a property of a material of an object.

Thus as per this theory, the material of this object undergoes failure when the maximum shear stress developed in an object (`\tau_{max}`) exceeds or becomes equal to the yield shear stress value in a uniaxial tensile test (`\tau_{\text{y. uniaxial}}`).

Thus to prevent failure, there should be,

Maximum shear stress ≤ yield shear stress (uniaxial)

`\tau_{max} \leq \tau_{\text{y. uniaxial}}`

As for uniaxial loading, `\tau_{\text{y. uniaxial}} = \frac{\sigma _{\text{yield}}}{2}`, the equation become,

`\tau_{max} \leq \frac{\sigma _{\text{yield}}}{2}`

This is the formula for the max shear stress theory.

Limitations of max shear stress theory:

• The theory is not suitable for the brittle material.
• It is not suitable for the hydrostatic loading.

• Read here: Maximum distortion energy theory

Maximum shear stress theory in three-dimensional loading:

The below figure shows the principal stresses (`\sigma_{1}, \sigma_{2}, \sigma_{3}`) for the object subjected to the triaxial loading. Each of the plane stress conditions has a maximum in-plane shear stress (`\tau_{12}, \tau_{23}, \tau_{31}`).

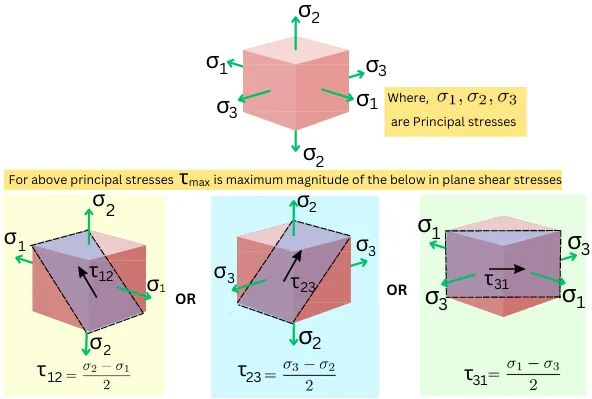
The maximum shear stress in triaxial loading is equal to a higher magnitude among the in-plane shear stresses, `\tau_{12}, \tau_{23}, \tau_{31}`.

`\therefore \tau_{max} = |\tau_{12}, \tau_{23}, \tau_{31}|`

`\tau_{max} = | \frac{\sigma _{1}-\sigma _{2}}{2},\frac{\sigma _{2}-\sigma _{3}}{2},\frac{\sigma _{1}-\sigma _{3}}{2}|\cdots[1]`

For uniaxial loading at the yield point, the relationship between yield stress and shear stress is given by,

`\tau_{\text{y. uniaxial}} = \frac{\sigma_{\text{yield}}}{2}\cdots[2]`

As per the statement of maximum shear stress theory, the object fails when,

`\tau_{max} \leq \tau_{\text{y. uniaxial}}`

Put values from [1] and [2] in the above equation,

`| \frac{\sigma _{1}-\sigma _{2}}{2},\frac{\sigma _{2}-\sigma _{3}}{2},\frac{\sigma _{1}-\sigma _{3}}{2}|\leq\frac{\sigma_{\text{yield}}}{2}`

Hence the conditions for the failure in three-dimensional force can be also written as,

`\frac{\sigma _{1}-\sigma _{2}}{2}\leq \frac{\sigma _{\text{yield}}}{2}`

`\frac{\sigma _{2}-\sigma _{3}}{2}\leq \frac{\sigma _{\text{yield}}}{2}`

`\frac{\sigma _{1}-\sigma _{3}}{2}\leq \frac{\sigma _{\text{yield}}}{2}`

By simplifying, the maximum shear stress theory equations can be written as,

`| \sigma _{1}-\sigma _{2} |\leq \sigma _{\text{yield}}`
`| \sigma _{2}-\sigma _{3} |\leq \sigma _{\text{yield}}`
`| \sigma _{1}-\sigma _{3} |\leq \sigma _{\text{yield}}`

Where, `\sigma_{1}, \sigma_{2}, \sigma_{3}` are the principal stresses.

Maximum shear stress theory for biaxial loading:

For biaxial loading one of the principal stress will become zero.

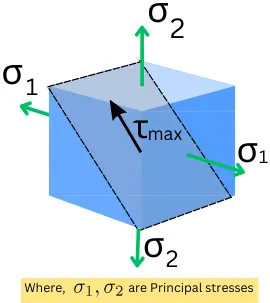
Hence by putting `\sigma_{3}` = 0 in the above three equations of triaxial loading, we get,

`| \sigma _{1}-\sigma _{2} |\leq \sigma _{\text{yield}}` —–(1)

`| \sigma _{2} |\leq \sigma _{\text{yield}}` —–(2)

`| \sigma _{1} |\leq \sigma _{\text{yield}}` —-(3)

These are the conditions for the maximum shear stress theory for biaxial stresses.

Note:- Condition 1 is considered when values of `σ_{1}` and `σ_{2}` are different, while conditions 2 or 3 are considered when `σ_{1}` and `σ_{2}` are same.

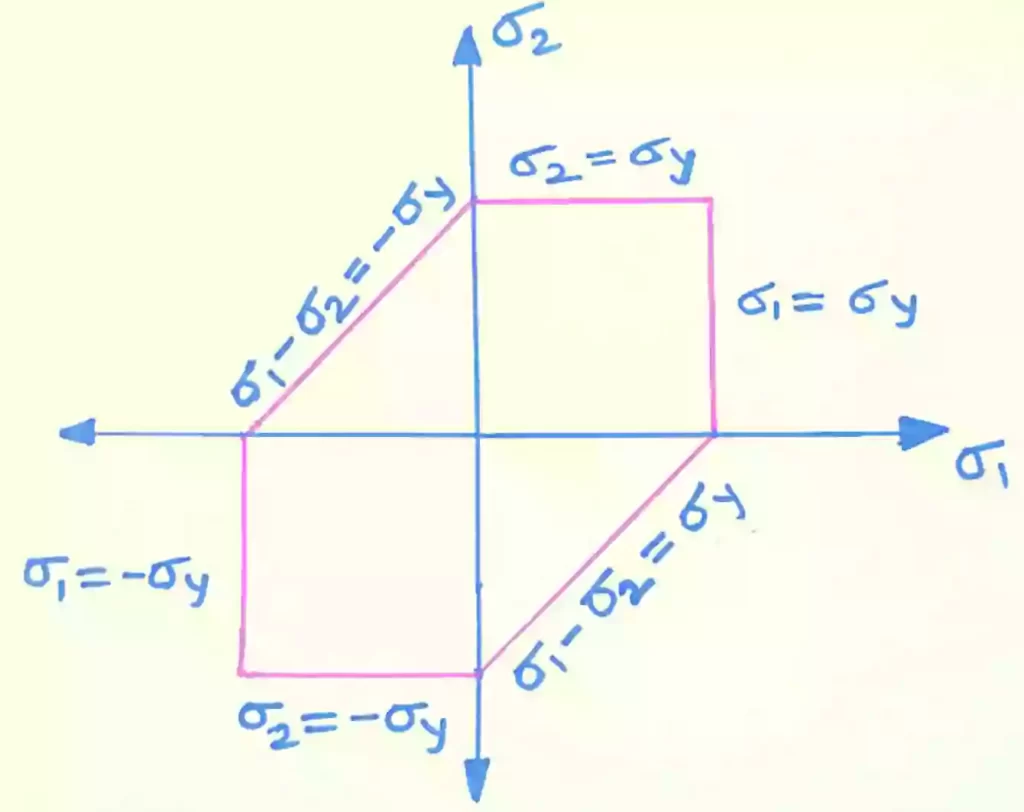
Yield surface for Maximum shear stress theory in biaxial loading:

For the tensile and compressive yield strength, the equations are written as,

Boundaries of region for tensile condition,

`| \sigma _{1}-\sigma _{2} |= \sigma _{\text{yield}}` ——(a)

`| \sigma _{2} |= \sigma _{\text{yield}}` ——(b)

`| \sigma _{1} |= \sigma _{\text{yield}}` ——(c)

For the compressive condition,

`| \sigma _{1}-\sigma _{2} |= -\sigma _{\text{yield}}` ——(d)

`| \sigma _{2} |= -\sigma _{\text{yield}}` ——(e)

`| \sigma _{1} |= -\sigma _{\text{yield}}` ——(f)

From these equations, the yield surface can be plotted as,

Maximum shear stress theory formula in form of axial stresses `(\sigma _{x}` and `\sigma _{y})`:

The condition for maximum shear stress failure in biaxial loading is,

`\sigma _{1}-\sigma _{2}=\sigma _{\text{yield}}`

But `\sigma _{1}` and `\sigma _{2}` are principal stresses which are given by,

`\sigma _{1}=\frac{\sigma _{x}+\sigma _{y}}{2}+\sqrt{(\frac{\sigma _{x}-\sigma _{y}}{2})^{2}+\tau_{xy}^{2}}`

`\sigma _{2}=\frac{\sigma _{x}+\sigma _{y}}{2}-\sqrt{(\frac{\sigma _{x}-\sigma _{y}}{2})^{2}+\tau_{xy}^{2}}`

Now, by putting the values of `\sigma_{1}` and `\sigma_{2}` in the equation of maximum shear stress theory we get,

`\sigma _{1}-\sigma _{2}=\sigma _{\text{yield}}`

`(\frac{\sigma _{x}+\sigma _{y}}{2}+\sqrt{(\frac{\sigma _{x}-\sigma _{y}}{2})^{2}+\tau_{xy}^{2}})-(\frac{\sigma _{x}+\sigma _{y}}{2}-\sqrt{(\frac{\sigma _{x}-\sigma _{y}}{2})^{2}+\tau_{xy}^{2}})=\sigma _{\text{yield}}`

`2\times \sqrt{(\frac{\sigma _{x}-\sigma _{y}}{2})^{2}+\tau_{xy}^{2}}=\sigma _{\text{yield}}`

`\sqrt{(\sigma _{x}-\sigma _{y})^{2}+4\tau_{xy}^{2}}=\sigma _{\text{yield}}`

This is the formula or condition of maximum shear stress theory for biaxial stresses.

Solved Numerical:

1] The loading on the object has values `σ_{x}` = 120 Mpa, `σ_{y}` = 60 Mpa, `\tau_{\text{xy}}` = 30 Mpa while the yield strength of the material of the object is 300 Mpa. Find the F.O.S. by using maximum shear stress theory?

Given:-

`σ_{x}` = 120 Mpa
`σ_{y}` = 60 Mpa
`\tau_{\text{xy}}` = 30 Mpa
`S_{yt}` = 300 Mpa

Solution:-

By using the formula for maximum shear stress theory for biaxial loading.

`\sigma _{\text{yield}}=\sqrt{(\sigma _{x}-\sigma _{y})^{2}+4\tau_{xy}^{2}}`

`\sigma _{\text{yield}}=\sqrt{(120-60)^{2}+4\times (30)^{2}}`

`\sigma _{\text{yield}}` = 84.85 Mpa

Now, the factor of safety is given by,

F.O.S.`=\frac{S_{yt}}{\sigma _{\text{yield}}}`

F.O.S.`=\frac{300}{84.85}`

F.O.S. = 3.53

 F.O.S. = 3.53 

Therefore the FOS by using the maximum shear stress theory is 3.53.

FAQs:

Read also:

• Conjugate beam method to find slope and deflection of beam
• Torsional shear stress meaning
• Torsional rigidity formula with unit
• Elastic constants of the material