Strain energy: Definition, Equation, Units, Examples, Explained with Pdf

Hey friends, in this article, we are going to discuss about strain energy and other details related to strain energy. When any object is subjected to different kinds of loads, it gets deformed elastically or plastically. The work done by external forces causes the deformation in the object. The energy absorbed during this work of deformation is known as strain energy.

In this article, we’re going to discuss:

1. What is Strain energy?
2. Strain energy formula:
3. Strain energy units:
4. Strain energy for different loadings:
   4.1. Strain energy due to axial load:-
   4.2. Strain energy due to bending load:-
   4.3. Strain energy due to shear load:-
   4.4. Strain energy due to torsional load:-
5. Strain energy density:
   5.1. Strain energy density formula:
   5.2. Strain energy density units:
6. Strain energy examples:

What is Strain energy?

Strain energy is the potential energy absorbed by the body due to the deformation or strain effect. It is denoted by the symbol uppercase letter ‘U’.

The strain energy absorbed by the material is equal to the work required to create the deformation in the object.

Therefore we can say that,

Strain energy = Deformation work

The strain energy is equal to the area under the load extension curve.

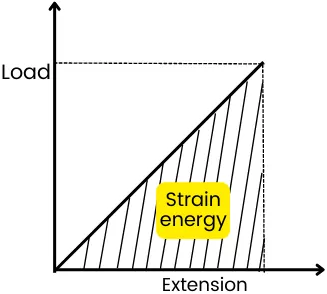
Thus from the above figure, the strain energy can be found as,

Strain energy = Area under load-extension curve = `\frac{1}{2}`.Load x Extension

The amount of strain energy absorbed by the material varies as per the method of application of load which are as follows,

1] Gradual load: In this case, the load on the material increases gradually from zero to max load.

2] Sudden load: In this case, the material is loaded suddenly with maximum load.

3] Impact load: In this case, the load is dropped from a certain height to cause strain in the object.

Strain energy formula:

The formula of strain energy varies as per the loading conditions.

1] Axial load:-

For member with constant cross-section and gradually applied load, the strain energy is given by,

U = `\frac{1}{2}P\delta_{L}`

Or

U = `\frac{P^{2}L}{2AE}`

Or

U = `\frac{\sigma^{2}V}{2E}`

Where,
P = Load applied
`\delta_{L}` = Change in length
A = Cross-sectional area
σ = Axial stress
L = Length of the component
V = Volume of component
E = Youngs modulus

For the member with variable cross-section area (`A_{x}`) and variable load (`P_{x}`) over length L, the strain energy is given by,

U = `\int_{0}^{L}\frac{P_{x}^{2}}{2A_{x}E}.dx`

2] Bending load:-

For pure bending moment over the component with the constant cross-sectional area, the strain energy is given by,

U = `\frac{M^{2}L}{2EI}`

Where,
M = Bending moment
L = Length of component
E = Modulus of elasticity
I = Moment of inertia

For the variable bending moment (`M_{x}`) and cross-section area (`A_{x}`), the strain energy is given by,

U = `\int_{0}^{L}\frac{M_{x}^{2}}{2A_{x}E}.dx`

3] Shear load:-

For gradually applied shear load over length L, the strain energy is given by,

U = `\frac{P^{2}L}{2AG}`

Where,
P = Shear load
A = Area of cross-section
G = Modulus of rigidity
L = Length of component

For variable shear load (`P_{x}`) over length L, the strain energy is given by,

U = `\int_{0}^{L}\frac{P_{x}^{2}}{2A_{x}G}.dx`

4] Torsional load:-

For gradually applied torsional load over length L, the strain energy is given by,

U = `\frac{T^{2}L}{2GJ}`

Or

U = `\frac{1}{2}T\theta`

Where,
T = Torque applied
L = Length of the shaft
J = Polar moment of inertia
G = Modulus of rigidity (Shear modulus)
θ = Angle of twist

For variable torsional load over length L, the strain energy is given by,

U = `\int_{0}^{L}\frac{T_{x}^{2}}{2GJ}.dx`

Strain energy units:

The strain energy is the potential energy stored in an object.

Thus the SI unit of strain energy is the Joule (J) or N.m and the FPS unit of strain energy is Btu or lb.ft

Strain energy for different loadings:

The strain energy for the different types of loading are as follows:-

Strain energy due to axial load:-

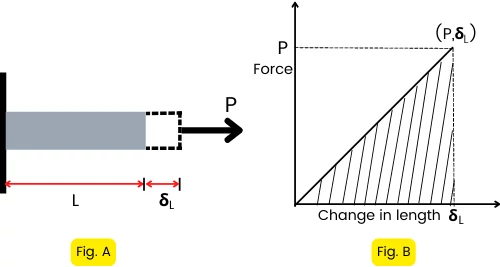
Figure A shows the member with a constant cross-sectional area loaded with axial load P.

The load applied in this condition is a gradual load from zero to P.

The elongation in the member with respect to force is shown in figure-B (force vs elongation graph).

The strain energy absorbed by an object is equal to the work done by the member against deformation and it can be found by calculating the area under the force vs elongation curve.

The shaded portion under the force-elongation curve has a triangular shape with an area of `\frac{1}{2}P\delta_{L}`, thus the strain energy can be given by,

Strain energy = `\frac{1}{2}P\delta_{L}`

As the change in length `\delta_{L}`=`\frac{PL}{AE}`, the formula can be modified as,

∴ Strain energy, U = `\frac{1}{2}P.(\frac{PL}{AE})`

∴ Strain energy, U = `\frac{P^{2}L}{2AE}`

Now by putting P = σA, the equation of strain energy can be modified as,

∴ Strain energy, U = `\frac{(\sigma A)^{2}L}{2AE}`

∴ Strain energy, U = `\frac{\sigma^{2} AL}{2E}`

But, AL = Volume of the object (V),

∴ U = `\frac{\sigma^{2} V}{2E}`

For the variable load or variable cross sectional area with respect to the length of object, the elemental strain energy is given by,

dU = `\frac{P_{x}^{2}}{2A_{x}E}`.dx

The total strain energy can be found as,

U = `\int_{0}^{L}\frac{P_{x}^{2}}{2A_{x}E}`.dx

Strain energy due to bending load:-

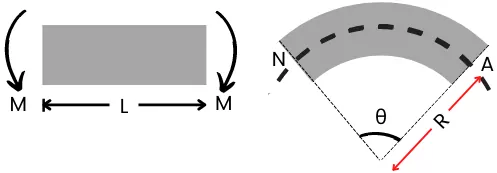
In the case of bending load applied to the component, the angle of curvature (θ) is considered as strain, and bending moment (M) is considered as load.

Therefore for the elastic component with a gradual increase in bending moment, the bending moment (M) vs angle of curvature (θ) can be plotted as follows,

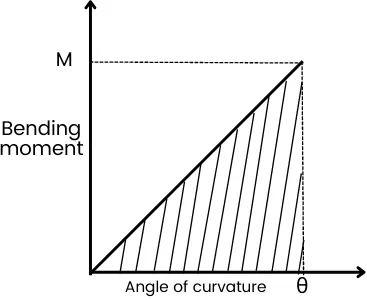
The strain energy for the bending load is equal to the area under this M-θ curve.

The shaded portion under the M-θ curve has a triangular shape with an area of `\frac{1}{2}M\theta`, thus the strain energy can be given by,

U = `\frac{1}{2}M\theta`

For the arc made at the neutral axis,

`\theta` = `\frac{L}{R}`

Put θ in the equation of strain energy,

Strain energy, U = `\frac{1}{2}\frac{ML}{R}`

From the bending equation,

`\frac{E}{R}` = `\frac{M}{I}`

∴ R = `\frac{EI}{M}`

Put this value of R in the equation of strain energy,

∴ Strain energy, U = `\frac{ML}{2(\frac{EI}{M})}`

U = `\frac{M^{2}L}{2EI}`

This is the equation for strain energy for the same cross-section and pure bending load.

For the variable bending moment (`M` = `M_{x}`), the elemental strain energy (dU) for the elemental length (L = dx) is given by,

dU = `\frac{M_{x}^{2}}{2EI}`.dx

Therefore total strain energy for variable load or variable cross-section is given by,

U = `\int_{0}^{L}\frac{M_{x}^{2}}{2EI}.dx`

Strain energy due to shear load:-

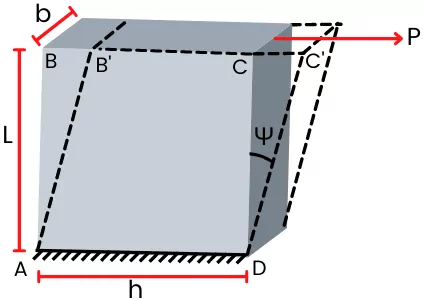
As shown in the figure, the shear force P is applied at the upper surface of the object.

This shear load is applied gradually from zero to P.

The strain energy in shear loading is given by,

U = Average load x Deformation

For the gradual load from zero to P, the average load is equal to the `frac{0 + P}{2}`. And the deformation in this case is equal to the CC’

Therefore the equation of the strain energy will become,

∴ U = `\frac{0 + P}{2}` x CC’

The shear strain (`\gamma`) for above object given by,

`\gamma` = tanΨ = `\frac{\text{CC’}}{CD}` = `\frac{\text{CC’}}{L}`

∴ CC’ = `\gamma`L

Put CC’ in equation of strain energy.

U = `\frac{P}{2}\gamma`L

But the shear strain `\gamma` is given by,

`\gamma` = `\frac{\tau}{G}`

Where,
G = Modulus of rigidity
𝜏 = Shear stress

Put the `\gamma` in the equation of strain energy.

U = `\frac{P}{2}(\frac{\tau}{G})L`

U = `\frac{P}{2G}(\frac{P}{A})L`

U = `\frac{P^{2}L}{2AG}`

This is the equation of the strain energy for the gradually applied shear load on the component with a constant area of a cross-section.

For the varying shear load along length L, the elemental strain energy for a smaller portion of length dx is given by,

dU = `\frac{P_{x}^{2}}{2AG}`.dx

The total strain energy for the varying shear load is calculated as,

U = `\int_{0}^{L} \frac{P_{x}^{2}}{2AG}`.dx

Strain energy due to torsional load:-

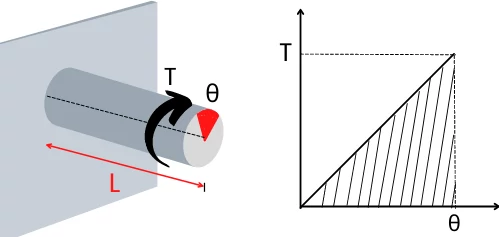
The above figure shows the elastic component under torsional load, loaded gradually from zero to T.

The elastic component shows torque vs angle of twist behavior as shown in the above T-θ graph.

The strain energy for this loading is equal to the area under this T-θ curve.

∴ Strain energy, U = `\frac{1}{2}` Tθ

The angle of twist (θ) can be given by,

θ = `\frac{TL}{JG}` —– (From torsional equation)

Put the value of θ in the equation of strain energy,

Strain energy, U = `\frac{1}{2}`T.(`\frac{TL}{JG}`)

U = `\frac{T^{2}L}{2GJ}`

This is the equation of strain energy for the constant torsional load over length L.

For the variable value of torque `T_{x}` along the length of the shaft, the elemental strain energy for a small portion of length dx is given by,

dU = `\frac{T_{x}^{2}}{2GJ}`.dx

The total strain energy is given by,

U = `\int_{0}^{L}\frac{T_{x}^{2}}{2GJ}`.dx

Strain energy density:

Strain energy density is the amount of strain energy absorbed per unit volume of the object. It is also known as the amount of work required to cause deformation in a unit volume of the object.

It is denoted by the symbol ‘u’ and it is equal to the area under the stress-strain curve.

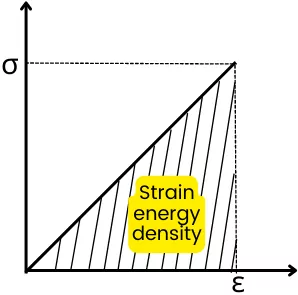
Therefore for the above stress-strain curve, the strain energy density can be calculated as,

u = `\frac{1}{2}\times\sigma.\varepsilon`

Strain energy density formula:

As per the definition of strain energy density,

u = `\frac{\text{Strain energy (U)}}{\text{Volume (V)}}`

The strain energy for axial load is given by,

U = `\frac{\sigma^{2} V}{2E}`

Therefore by putting strain energy in equation of strain energy density,

u = `\frac{U}{V}`

u = `\frac{\frac{\sigma^{2} V}{2E}}{V}`

∴ u = `\frac{\sigma^{2}}{2E}`

The strain energy density in the form of stress (σ) and strain (ε) is given by,

u = `\frac{1}{2}\times\sigma\varepsilon`

Strain energy density units:

SI system:-

In SI unit system, the unit of strain energy is the joule (J), and the unit of volume is m³.

∴ u = `\frac{U}{V}` = `\frac{J}{m^{3}}` = J/m³

∴ The SI unit of strain energy density is J/m³.

FPS system:-

In FPS system, the unit of strain energy is Btu and unit of volume is ft³.

∴ u = `\frac{U}{V}` = `\frac{Btu}{ft^{3}}` = Btu/ft³

∴ The FPS unit of strain energy density is Btu/ft³.

Strain energy examples:

The aluminum rod of 10 mm diameter and 1 m in length is subjected to the axial load. The load is applied gradually from 0 to 26 KN. If E = 68.5 Gpa, Find strain energy and strain energy density in the aluminum rod.

Given:-
d = 10 mm = 0.01 m
L = 1 m
P = 26 KN = 26 x 10³ N
E = 68.5 Gpa = 68.5 x 10⁹ N/m²

Solution:

For gradual application of load, the resulting strain energy is given by,

U = `\frac{P^{2}L}{2AE}`

The cross-sectional area (A) is given by,
A = `\frac{\pi }{4}d^{2}`
A = `\frac{\pi }{4}.(0.01)^{2}`
A = 7.85 x 10⁻⁵ m²

Put the values into the strain energy equation,

U = `\frac{(26 \times 10^{3})^{2} \times 1}{2 \times 7.85 \times 10^{-5} \times 68.5 \times 10^{9}}`

U = 62.857 J

This is the strain energy absorbed by the aluminum rod.

The strain energy density of the object is given by,

u = `\frac{U}{V}` = `\frac{U}{AL}`

u = `\frac{62.857}{(7.85 \times 10^{-5}) \times 1}`

u = 800.72 x 10³ J/m³

This is the strain energy density absorbed by the aluminum rod.

FAQ’s

Print / PDF