The key difference between principal stress vs bending stress is that principal stress indicates maximum and minimum normal stress on the object while bending stress indicates stress arises due to the bending load.
Before moving on to our main topic, let’s have a quick look at each of them.
Contents:
Principal stress:
Principal stress is the stress acting on the principal plane whereas the principal plane is the plane that possesses only normal stress and no shear stress.
Look at the member shown in below Fig-A. It experiences axial stresses in x and y direction (`\sigma_{x}, \sigma_{y}`) and complementary shear stresses (`\tau_{xy}, \tau_{yx}`).
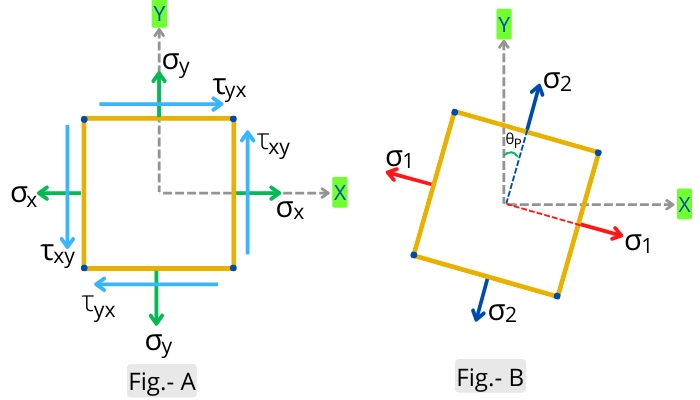
Each plane in above figure-A is experiencing normal force and shear force. Other than these planes, the member also has a number of planes.
As shown in figure-B, a specific plane inclined at angle `\theta_{P}` has no shear stress and has only normal stress acting on it. Such a plane is known as a principal plane and the normal stress on that plane is known as the principal stress.
The `sigma_{1}` and `sigma_{2}` in the above figure are the major and minor principal stresses respectively.
Bending stress:
Bending stress is the internal resistance developed by the object to resist the deformation caused by the bending moment.
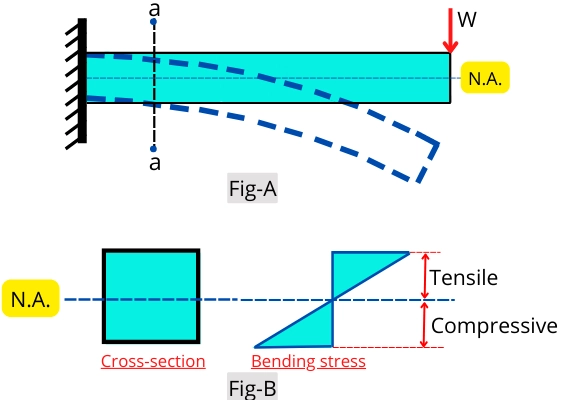
The above figure-A shows the cantilever beam subjected to the bending load and fig-B indicates the distribution of bending stress over the cross-section at a location a – a.
The above figure-B indicates that the bending stress never gets uniformly distributed over the cross-section. It is negligible at the neutral axis position and maximum at the upper and lower surfaces.
The bending stresses on either side of the neutral axis are opposite in nature. It means that if the bending stress above the neutral axis is tensile in nature then the bending stress below the neutral axis is compressive.
For the cross-section shown in above figure-B, the bending stress `\sigma_{b}` is given by,
`\sigma_{b} = \frac{M}{I} \times y`
Where,
M = Bending moment at section a-a
I = Moment of inertia about the neutral axis (N.A.)
y = Distance between N.A. and location where `\sigma_{b}` has to find
Principal stress vs Bending stress:
| Sr. No. | Principal stress | Bending stress |
|---|---|---|
| 1 | The normal stresses acting on the principal planes are known as principal stresses. | It is stress developed by an object to resist deformation due to bending load. |
| 2 | It arises due to the application of axial forces and complementary shear forces. | It arises due to the application of bending moment. |
| 3 | It is used as a criterion for theories of failure. | It is not used in theories of failure. |
| 4 | It is useful for the design of brittle materials. | It is used for the analysis of the object subjected to the bending load. |
| 5 | It is calculated at the principal planes. | It is calculated at the plane perpendicular to the neutral axis of the beam. |
FAQ:
Why principal stress and bending stress are important?
The principal stress is an important failure criterion for the design of brittle materials, whereas the bending stress is important in the design of a member subjected to a bending moment.
Related articles: