Principal stress vs Normal stress – Difference [Explained]

One of the vital distinguishing points for principal stress vs normal stress is that the principal stress is the normal stress acting on the principal plane of the member, while normal stress is the axial stress that arises in the object to resist the deformation in the axial direction.

Let’s take a quick look at each of them before we get to our topic.

In this article, we’re going to discuss:

• Principal stress:
• Normal stress:
• Principal stress vs Normal stress:
• FAQ:

Principal stress:

In simple words, the normal stress on principal planes is known as principal stress, while the principal planes are the geometric plane in the object at which no shear stress is acting.

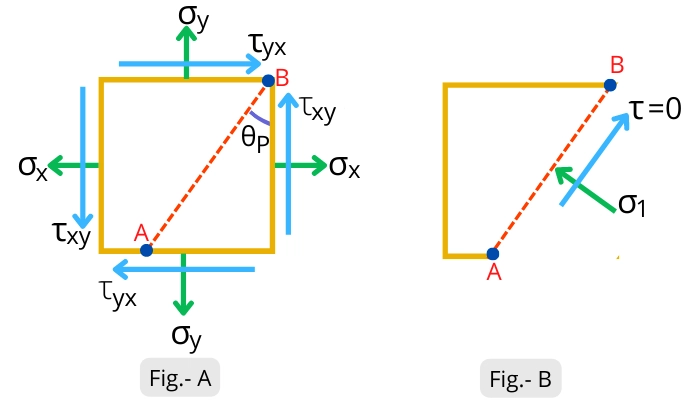
The above Fig-A shows the object subjected to the bi-axial stress. In this figure, the plane AB indicates one of the principal planes inclined at angle `\theta_{P}`.

The Fig-B shows the stresses acting on the principal plane AB. As discussed before, the shear stress acting on the principal plane is zero while the normal stress on the principal plane (`\sigma_{1}`) is known as principal stress.

For a biaxial stress situation, there are two principal planes, and the principal stresses acting on each of these planes are known as Maximum principal stress (`\sigma_{1}`) and Minimum principal stress (`\sigma_{2}`).

The equation for each of the principal stress is given by,

`\sigma_{1} = (\frac{\sigma_{x}+\sigma_{y}}{2}) + \sqrt{(\frac{\sigma_{x}-\sigma_{y}}{2})^{2} – \tau_{xy}^{2}}`

`\sigma_{2} = (\frac{\sigma_{x}+\sigma_{y}}{2}) – \sqrt{(\frac{\sigma_{x}-\sigma_{y}}{2})^{2} – \tau_{xy}^{2}}`

Normal stress:

Normal stress is the stress developed into the object when the object is subjected to axial loading. It generally acts in a normal direction to the plane.

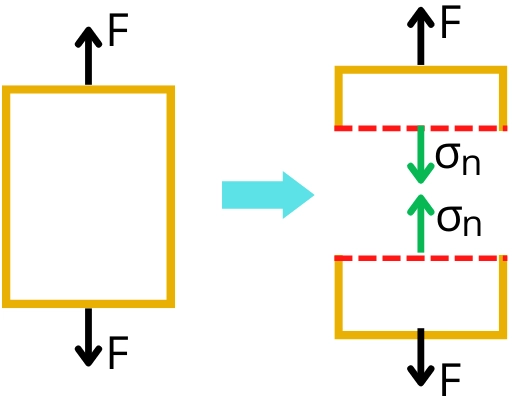
As shown in the above figure, these stresses are axial and it may be of tensile or compressive nature.

It is generally calculated as,

`\sigma = \frac{\text{Normal resistive force}}{\text{Area}}`

Principal stress vs Normal stress:

Sr. No.	Principal stress	Normal stress
1	These are the normal stresses on the principal planes.	It is the stress acting perpendicular to the plane.
2	It is used in one of the theories of failure to predict the failure in brittle materials.	It is not used for the failure criteria.
3	The planes on which principal stresses act has zero shear stresses.	The planes on which normal stress acts may or may not have shear stresses.
4	The principal stress indicates maximum and minimum normal stress acting on the member.	The normal stress indicates the stress developed by the object against axial forces.
5	In the biaxial stress condition, the principal stresses are present on a maximum of two planes.	In the biaxial stress condition, there are multiple planes in an object which experience normal stress.

FAQ:

Related article:

• Difference between principal and bending stress