Mohr’s circle explained, Learn how to draw it

Mohr’s circle is the graphical method for finding the stresses at different oblique planes and this method requires less time and calculations than the analytical method to find stresses at different oblique planes.

What is mohr’s circle?

Mohr’s circle represents the graphical form of the transformation law. The mohr’s circle is the easiest method for finding the principal stresses and normal stresses at various planes.

Each point on the circumference of mohr’s circle represents a certain plane which gives the value of normal stress and shear stress at that plane.

Therefore the value of normal stress along with the shear stress indicates the particular plane of the object.

The mohr’s circle can be drawn for the biaxial stresses and also for the triaxial stresses.

Mohr’s circle uses and significances:

The mohr’s circle method has the following uses and significances:-

1] By drawing a single mohr’s circle, we can easily find normal and shear stresses at various inclined oblique planes which is difficult by using the analytical method.

2] By using mohr’s circle, it is easy to calculate principal stresses, maximum shear stress, resultant stress, principal plane angle, etc.

3] The method of mohr’s circle is a simple and faster method than the analytical method.

Sign conventions for mohr’s circle:

For normal stress:-

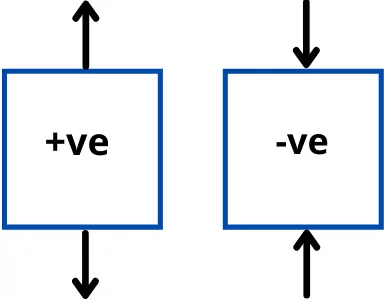
Tensile stress is considered as +ve and compressive stress is considered as -ve.

For shear stress:-

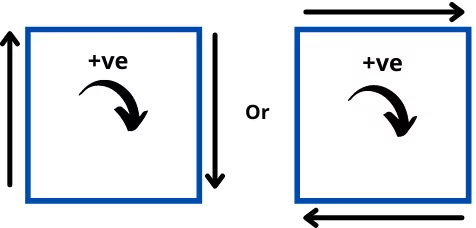
1] If shear stresses are of clockwise nature then it is considered as positive.

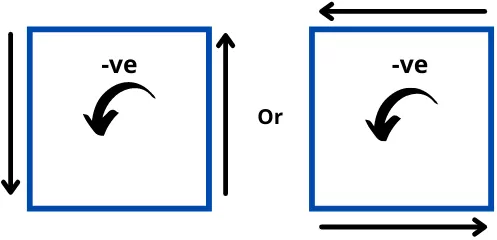
2] If shear stress is anticlockwise in nature then it is considered as negative.

For oblique angle:-

1] If the angle is measured in a clockwise direction from the reference plane then it is considered as positive.

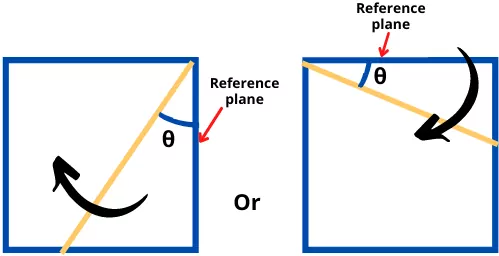
2] If the angle is measured in an anticlockwise direction from the reference plane then it is considered as negative.

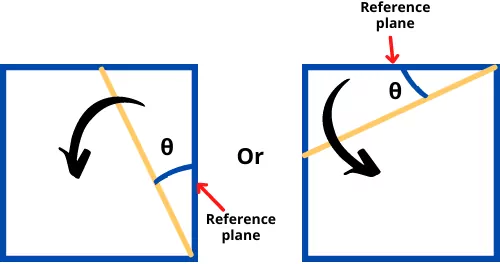
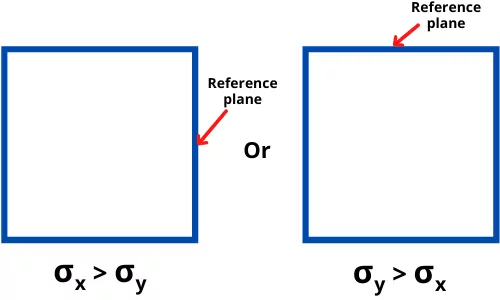
How to identify the reference plane?

The plane which has maximum axial stress is considered as a reference plane.

If `\sigma_{x}` > `\sigma_{y}` then vertical plane is considered as reference plane.

If `sigma_{y}` > `\sigma_{x}` then horizontal plane is considered as reference plane.

How to draw mohr’s circle?

Consider an example with stresses as shown below with `\sigma_{x}` > `\sigma_{y}`.

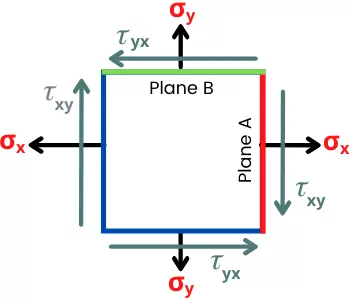
The plane ‘A’ shown by red color is the reference plane (as `\sigma_{x}` > `\sigma_{y}`) at 0°. The plane B shown by green color is the horizontal plane at 90° clockwise.

The steps to draw the Mohr’s circle from the normal and shear stresses are as follows:-

Step 1] Draw, the vertical and horizontal axis with normal stress (`\sigma_{n}`) as abscissa and shear stress (`\tau`) as ordinate with the suitable scale.

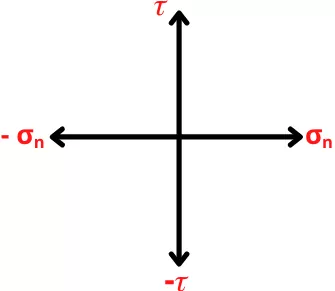
Step 2] Locate plane A on `\sigma_{n}` – `\tau` plot.

First locate `\sigma_{x}` on `\sigma_{n}` axis. If the `\sigma_{x}` is tensile then locate it on positive `\sigma_{n}` axis from origin. And if the `\sigma_{x}` is compressive then locate it on negative `\sigma_{n}` axis from origin.

From the endpoint of the `\sigma_{x}`, draw `\tau_{xy}` in the vertical direction. If the nature of `\tau_{xy}` is clockwise then draw it in positive `\tau` direction and if the nature of `\tau_{xy}` is anticlockwise then draw it in negative `\tau` direction.

For the given example, plane A is located as A (+ `\sigma_{x}`, + `\tau_{xy}`), as shown in the below figure.

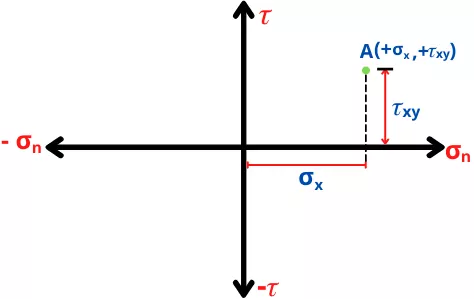
Step 3] Locate plane B on `\sigma_{n}` – `\tau` plot.

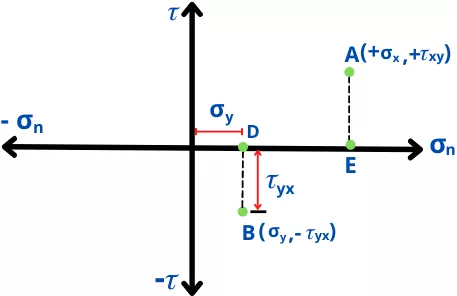
Similarly, plot the plane B on `\sigma_{n}` – `\tau` plot.

For the given example, plane B is located as B(`\sigma_{y}`, -`\tau_{yx}`).

Step 4] Join points A and B.

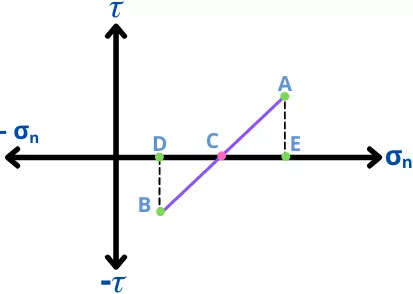
Step 5] Draw a circle with radius AC or BC with C as the center of the circle.

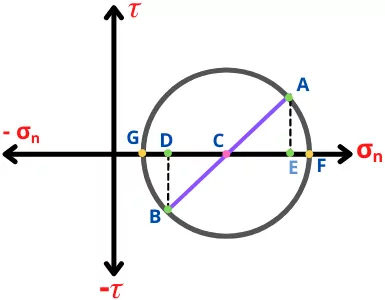
In this figure, point A indicates plane A while point B indicates plane B.

What are the principal stresses on a mohr’s circle?

The principal stresses are the normal stresses when the value of shear stress (`\tau`) is zero. On the mohr’s circle, there are two points that are ‘F’ and ‘G’.

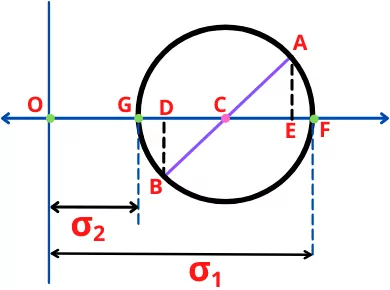
Therefore the major principal stress is,

`\mathbf{\sigma_{1}}` = Distance OF

And the minor principal stress is,

`\mathbf{\sigma_{2}}` = Distance OG

Maximum shear stress from mohr’s circle:

The magnitude of maximum shear stress (`\tau_{max}`) is equal to the radius of mohr’s circle in the verticle direction.

To find maximum shear stress from mohr’s circle, follow the steps given below:-

1] Draw a perpendicular line to the `\sigma_{n}` axis from the center ‘C’ of mohr’s circle.

2] Find the value of shear stress at the point where the perpendicular line cuts the mohr’s circle.

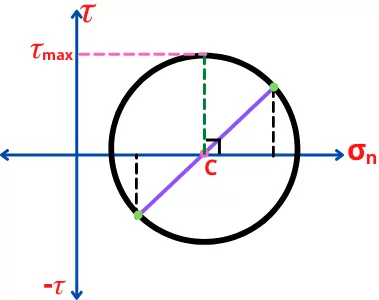
Or by using principal stresses, the maximum shear stress can be calculated as,

`\tau_{\text{max}}` = `\frac{\sigma_{1}-\sigma_{2}}{2}`

Stresses at the oblique plane by using mohr’s circle:

In the mohr’s circle, the angle of the oblique plane is double of actual angle.

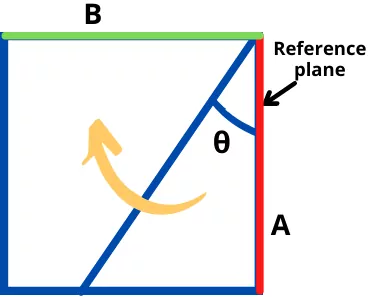
In the stress diagram, if the angle of the oblique plane (θ) is measured anticlockwise from the reference plane then in mohr’s circle diagram the oblique plane should be drawn with an angle (2θ) measured anticlockwise from a reference plane.

In the stress diagram, if the angle of an oblique plane (θ) is measured clockwise from the reference plane then in mohr’s diagram, the oblique plane should be drawn with angle (2θ) measured clockwise from a reference line.

The example of the oblique plane at a clockwise angle (θ) is shown below.

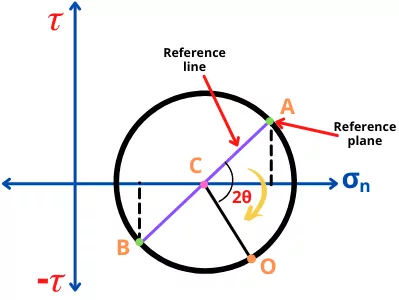
Now after drawing the oblique plane on mohr’s circle, draw perpendicular lines on the `\sigma_{n}` and `\tau` axis to get the values of normal stress and shear stress at this oblique angle.

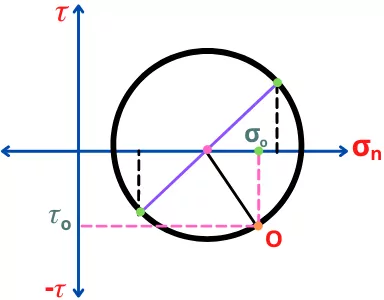
Here `\sigma_{o}` and `\tau_{o}` are normal stress and shear stress for the oblique plane at angle θ.

Mohr’s circle for different cases:

Following are the different special cases of the mohr’s circle:-

Case I: Mohr’s circle for pure shear stresses:-

For the object subjected to only shear stresses (pure shear), the stress diagram is drawn below,

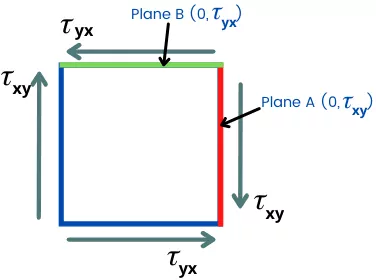
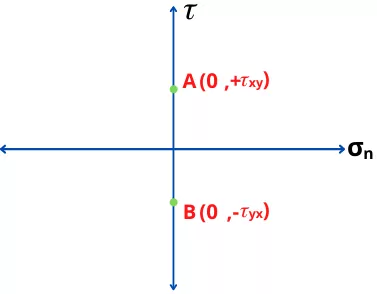
For zero normal stresses, plane A and plane B has the following coordinates on Mohr’s circle

A = (0, `\tau_{xy}`)
B = (0, -`\tau_{yx}`)

The point A and B can be plotted on `\sigma_{n}` – 𝜏 graph as follows,

The line AB intersects the `\sigma_{n}` axis at point C. Thus draw a circle with a radius of ‘AC’ and ‘C’ as the center of the circle.

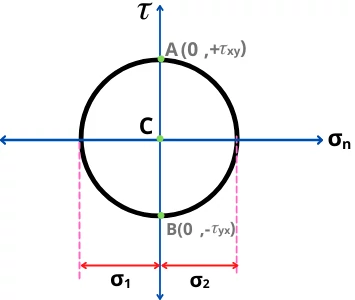
In this case, the relation between principal stresses is given by,

`\mathbf{\sigma_{1} = -\sigma_{2}}`

Case II: Mohr’s circle for only normal stresses:-

For the object subjected to only normal stresses and zero shear stresses (`\tau_{xy} = \tau_{yx}` = 0), the stress diagram is drawn below,

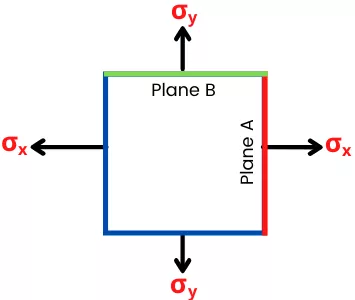
For zero shear stresses, plane A and plane B has the following coordinates on Mohr’s circle

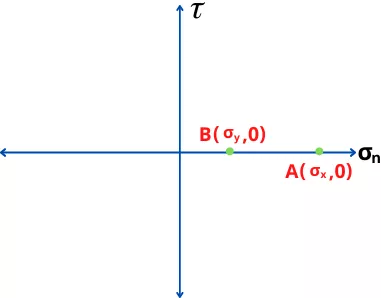
A = (`\sigma_{x}`, 0)
B = (`\sigma_{y}`,0)

The point A and B can be plotted on `\sigma_{n}` – 𝜏 graph as follows,

Divide the line ‘AB’ and find the center of Mohr’s circle. Draw a circle with ‘C’ as the center and ‘AC’ as the radius of Mohr’s circle.

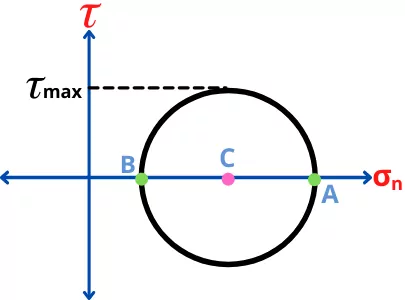
In this case, the maximum shear stress is given by,

`\mathbf{\tau_{max} = frac{\sigma_{x}-\sigma_{y}}{2}}`

Case III: Mohr’s circle for zero shear stresses and same normal stresses:-

If the normal stresses `\sigma_{x}` and `\sigma_{y}` are equal (`\sigma_{x} = \sigma_{y}`) and there is no shear force is acting on the object, (`\tau_{xy}` = `\tau_{yx}` = 0) then in this situation both plane A and B lies on same location.

Therefore the diameter of mohr’s circle becomes zero and in this situation, the mohr’s circle becomes a point.

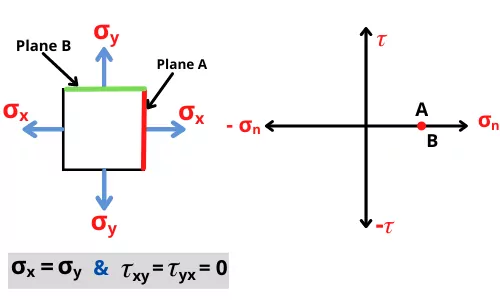
Mohr’s circle example:

1] For the given stress condition, find the principal stresses by using mohr’s circle method.

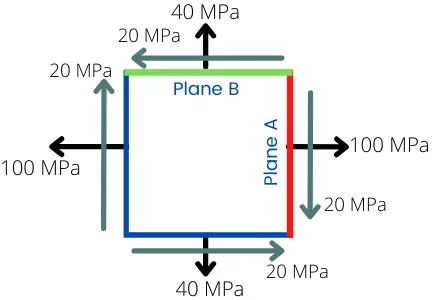
Given:
`\sigma_{x}` = 100 Mpa
`\sigma_{y}` = 40 MPa
`\tau_{xy}` = 20 MPa (Clockwise)
`\tau_{yx}` = -20 MPa (Anticlockwise)

Solution:-

Steps to draw mohr’s circle:–

1] Draw `\sigma_{n}` and `\tau` axis with suitable scale.

2] Plot plane ‘A’ with coordinates of A(100, 20).

3] Plot plane ‘B’ with coordinates of B(40, -20).

4] Join points ‘A’ and ‘B’.

5] The line AB intersects the `\sigma_{n}` axis at point ‘C’.

6] Draw a circle with ‘C’ as the origin and ‘AC’ as radius.

7] Measure distance ‘OG’ and ‘OF’
As, `\sigma_{1}` = OF and `\sigma_{2}` = OG

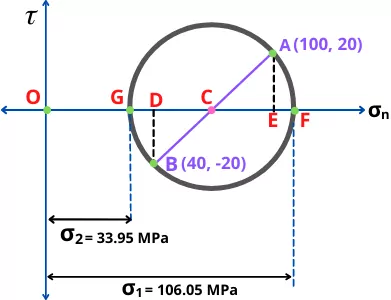
Therefore from above Mohr’s circle, principal stresses are,

`\mathbf{\sigma_{1}}` = OF = 106.05 MPa
`\mathbf{\sigma_{2}}` = OG = 33.95 MPa

FAQ’s

Read also:

• Maximum shear stress theory explained
• Von mises stress theory statement