If I tell you to cut the rubber piece with a knife, you can simply cut it into two or more pieces with no effort. But if I tell you to cut the steel bar with the same knife, you won’t even be able to scratch it. The different behaviors of these materials are associated with their elastic property known as shear modulus. So in this article, we are going to discuss the term shear modulus in detail.
Contents:
What is shear modulus?
Shear modulus also known as modulus of rigidity is the ratio of the shear stress to the shear strain under the elastic limit.
It reflects the stiffness of the material to resist the deformation occurring due to the application of shear stresses.
Shear modulus gives the relation between the shear stress applied and the shear strain developed into the material.
It is denoted by the symbol G or C or N.
Shear modulus explained:
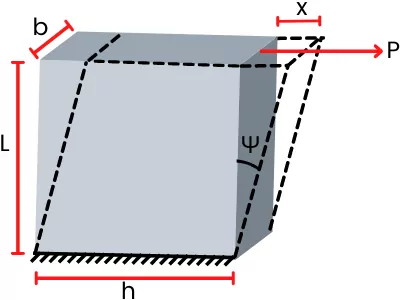
As shown in the above figure, the bottom of the object is fixed to the rigid support, and the parallel force P is applied at the top of the object. This parallel force develops shear stress into the object that is given by,
`\tau ` = `\frac{\text{Shear force}}{\text{Shear area}}` = `\frac{P}{A}`
Due to this shear force, the material of the object undergoes deformation by changing its shape. In the above figure, the top layer of the object gets displaced by distance x.
Thus, in this case, the shear strain is given by,
Shear strain, (`\gamma`) = tan(ψ) = `\frac{x}{L}`
Hooke’s law in the form of shear stress states that the shear stress (𝜏) is directly proportional to the shear strain (`\gamma`) within the elastic limit.
∴ `\tau` ∝ `\gamma`
`\tau = G.\gamma`
Where G is the elastic constant known as shear modulus, that is given by,
G = `\frac{\tau}{\gamma}`
The formula can be modified by putting the values of shear stress and shear strain.
∴ G = `\frac{P/A}{x/L}`
∴ G = `\frac{PL}{Ax}`
Shear modulus equation:
The shear modulus of the material can be calculated by use of the following formula.
G = `\frac{\text{Shear stress}}{\text{Shear strain}}` = `\frac{\tau}{\gamma}`
Or
G = `\frac{PL}{A.x}`
Where,
P = Shear force
L = Height of the object perpendicular to the shear force
A = Shear area
`x` = Top layer displacement with respect to the bottom layer
Shear modulus units:
SI unit:
In the SI system, the unit of shear stress is N/m² or Pascal and the shear strain is the unitless quantity.
Therefore,
Shear modulus, G = `\frac{\tau}{\gamma}` = N/m²
Thus the SI unit of the shear modulus or modulus of rigidity is N/m² or Pascal.
FPS Unit:
In the FPS system, the unit of shear stress is lb/ft² and the shear strain is the unitless quantity.
Therefore,
Shear modulus, G = `\frac{\tau}{\gamma}` = lb/ft²
Thus the FPS unit of the shear modulus or modulus of rigidity is lb/ft².
Shear modulus dimensional formula:
The dimensional formula of the shear stress is [M¹L⁻¹T⁻²]
The shear strain is a unitless quantity, therefore the dimensional formula for the shear strain is [L⁰M⁰T⁰]
Therefore the dimensional formula for the shear modulus is given by,
G = `\frac{\text{Shear stress}}{\text{Shear strain}}` = `\frac{[M¹L⁻¹T⁻²]}{[L⁰M⁰T⁰]}`
∴ G = [M¹L⁻¹T⁻²]
Hence the dimensional formula of the shear modulus is [M¹L⁻¹T⁻²].
How to calculate shear modulus?
Following are some methods to calculate the shear modulus:-
A] If the values of shear stress and shear strain are known, then by using the following formula we can calculate the shear modulus.
G = `\frac{\text{Shear stress}}{\text{Shear strain}}` = `\frac{\tau}{\gamma}`
B] The slope of the shear stress vs shear strain curve up to the proportionality limit gives the shear modulus.
C] By using the relations between the elastic constants it is easy to calculate the shear modulus.
How to calculate modulus of rigidity from stress strain curve?
The curve of the shear stress vs shear strain is linear up to the proportionality limit.
Thus the slope of this shear stress vs shear strain curve up to the proportionality limit is the shear modulus of the material.
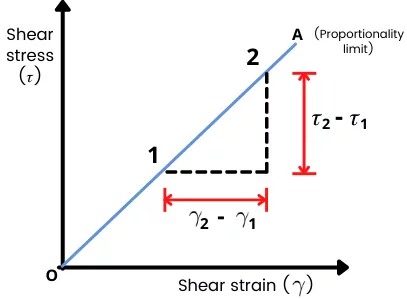
From the above graph, the shear modulus can be calculated as,
G = Slope [OA] = `\frac{\tau_{2} – \tau_{1}}{\gamma_{2} – \gamma_{1}}`
How to calculate shear modulus by using relations between elastic constants?
The modulus of rigidity (G) can be calculated by using the relations between elastic constants. The relations between elastic constants are listed below.
E = 2G(1 + 𝒗)
Or
E = 9KG/(3K + G)
Where,
𝒗 = Poisson’s ratio
K = Bulk modulus
E = Young’s modulus
Shear modulus problems with solutions:
The square plate of side length 1 m and 0.4 m thickness is kept vertical with the bottom surface fixed to the rigid support. After the application of 50 KN of parallel shear force at the top of the plate, the top surface gets displaced by 1 mm in comparison with the bottom surface. Find the shear modulus of the material used for the plate.
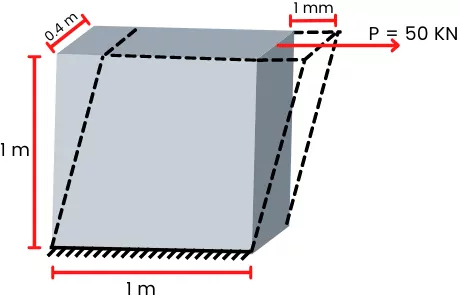
Given:
L = 1 m
h = 1 m
b = 0.4 m
P = 50 KN = 50 x 10³ N
X = 1 mm = 1 x 10⁻³ m
Solution:-
Area of the plate subjected to shear stress is given by,
A = h x b = 1 x 0.4 = 0.4 m²
Shear stress applied in the plate is given by,
`\tau ` = `\frac{P}{A}` = `\frac{50 \times 10^{3}}{0.4}` = 125 `\times 10^{3}` N/m²
Shear strain is given by,
`\gamma ` = `\frac{x}{L}` = `\frac{1 \times 10^{-3}}{1}` = 1 `\times 10^{-3}`
Modulus of rigidity (G) is given by,
G = `\frac{\tau}{\gamma}` = `\frac{125\times10^{3}}{1 \times 10^{-3}}`
G = 125 x 10⁶ N/m² = 1.25 GPa
FAQ’s
-
What is the relationship between Young’s modulus and shear modulus?
The young’s modulus and shear modulus are elastic constants and the Relation between these elastic constants is given by the following equation:-
E = 2G(1 + 𝒗)
Where,
E = Young’s modulus
G = Shear modulus
𝒗 = Poisson’s ratio -
Is shear modulus the same as modulus of rigidity?
The ratio of shear stress to shear strain is known as the shear modulus, often known as the modulus of rigidity.
-
Is shear modulus a material property?
The shear modulus is the material property that shows the stiffness of the material against shape change.