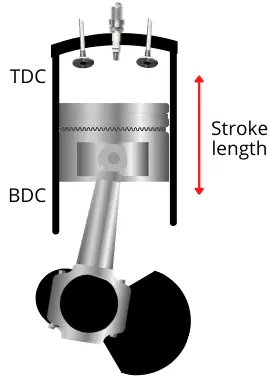
What is stroke length in ic engine?
The stroke length is the distance travels by the piston inside the engine cylinder from Top dead center to the Bottom dead center or from the Bottom dead center to Top dead center.
The stroke length is denoted by the ‘L’.
Based on the relation between the stroke length and the bore, the engines are divided into the following types.
- Oversquare engines: IC engines that have a long bore than the stroke are known as oversquare engines.
- Square engines: The engines that have the same stroke and the bore is known as square engines.
- Undersquare engines: The engines which have a long stroke than the bore are known as undersquare engines.
Contents:
What is stroke formula?
The distance traveled by the piston during its one stroke is known as the stroke length and the formula of the stroke length is,
L = `\frac{ED\ (\text{CC})}{\frac{\pi }{4}\times B^{2}\times N}`
Where,
N = Number of cylinders
B = Cylinder bore in centimeter
ED (CC) = Engine displacement in Cubic centimeter
How to calculate stroke length of an engine?
The stroke length formula is given by,
L = `\frac{ED\ (\text{CC})}{\frac{\pi }{4}\times B^{2}\times N}`
For calculating the stroke length, we require the values of the following three terms related to the engine:-
- Engine displacement
- Cylinder bore
- Number of cylinders
If we have these values, then simply by putting these values in the above equation of stroke length and solving it, we can easily find the engine’s stroke length.
Example:
If the double cylinder 100 CC engine has a cylinder bore of 4 cm, then calculate the stroke length of the engine.
Solution:-
Given:
Engine displacement, [ED(CC)] = 100 CC
Bore, (B) = 4 cm
Number of cylinders, (N) = 2
The stroke length of the engine is given by,
L = `\frac{ED\ (\text{CC})}{\frac{\pi }{4}\times B^{2}\times N}`
By putting the all given values in above equation, we get,
= `\frac{100}{(\frac{\pi }{4})\times 4^{2}\times 2}`
By solving the equation, we get,
L = 3.98 cm
Hence the stroke length of the engine is 3.98 cm.