Thermal boundary layer: Definition, Thickness equation [with Pdf]

What is Thermal boundary layer?

When the free stream of fluid at temperature ‘`T_{\infty}`’ approaches to the plate at different temperature ‘`T_{s}`’ that is `T_{\infty}` ≠ `T_{S}`, then the thermal boundary layer is generated.

It is the region in which a temperature gradient (dT/dy) is present in the direction perpendicular to the flow of the free stream.

Thermal boundary layer generation:

The thermal boundary layer exists only when the temperature of the free stream and the surface of the plate are not equal.

Case 1: If `\mathbf{T_{\infty}>T_{S}}`:–

Following is the profile of the thermal boundary layer when the free steam temperature is higher than plate temperature.

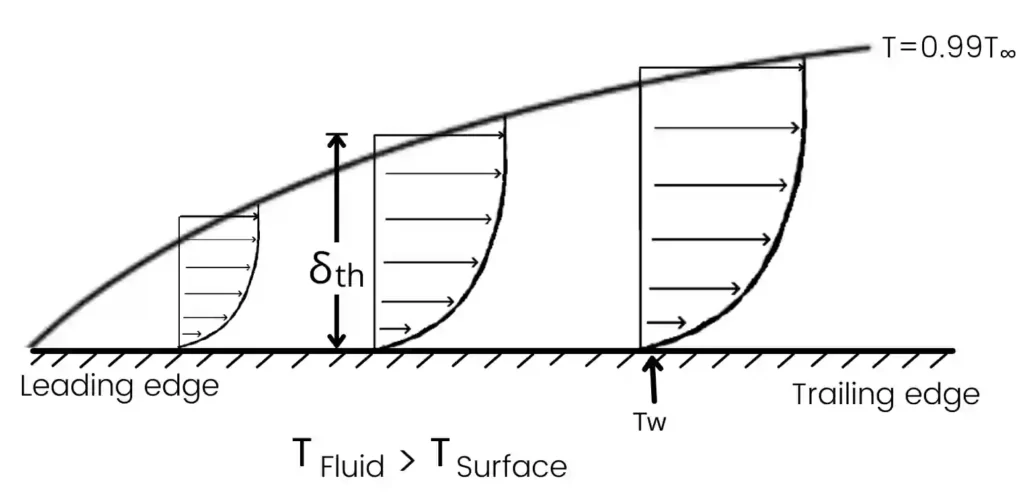
The free stream of fluid at temperature `T_{\infty}` touches the plate at the leading point.

1) In this profile the temperature of the fluid layer closed to the plate is almost equal to the plate temperature ( `T\ \approx\ T_{\infty}` ). As the layer nearest to the plate has negligible velocity therefore in this case the heat transfer is done by conduction.

2) As we move in a forward direction the temperature of lead also rises layer by layer.

3) At a distance y = `δ_{th}` the temperature of the fluid is almost equal to the temperature of the free stream.

4) Therefore the distance `δ_{th}` is known as boundary layer thickness at which,

`T-T_{s}=0.99(T_{\infty}-T_{s})`

5) Above the distance y = `δ_{th}` the temperature of the fluid remains constant and equals to the temperature of the free stream.

6) If we move ahead in the downstream direction (x-direction) then the thickness of the boundary layer also goes increasing due to the retardation of fluid particles in the downstream direction.

7) If we join points of `δ_{th}` from x = 0 to x = L then the curve generated is known as `δ_{th}` (x) curve.

8) The region under the `δ_{th}` (x) curve is known as the thermal boundary layer. While the region outside of the `δ_{th}` (x) curve is known as the outer flow region.

Boundary conditions for `\mathbf{T_{\infty}>T_{S}}`:

The boundary conditions for boundary layer region are,

a) At y = 0, T = Ts
b) At y = `δ_{th}`, (`T` – `T_{s}`) = 0.99 (`T_{\infty}` – `T_{s}`)
c) At y > `δ_{th}`, T = `T_{\infty}`
d) At x = 0, `δ_{th}` = 0

Case 2: If `\mathbf{T_{S}>T_{\infty}}`:-

The boundary layer region for surface temperature greater than free stream temperature can be plotted as,

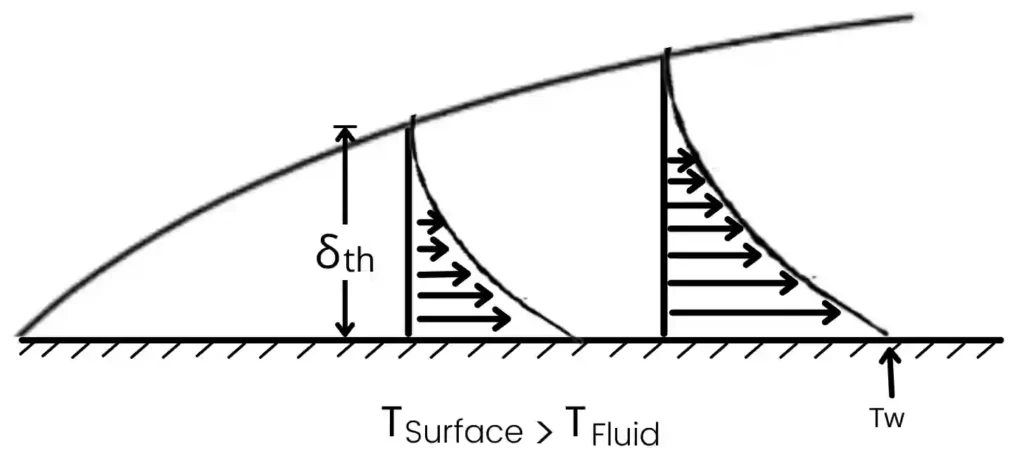
1) As shown in the profile the temperature of the layer adjacent to the plate has a temperature equal to the plate temperature.

2) As we move in an upward direction the temperature of fluid decreases layer by layer.

3) At y = `δ_{th}` the temperature of the fluid is near equal to the free stream temperature.

Boundary conditions at `\mathbf{t_{S}\ > t_{\infty}}`:

In this case, the boundary conditions are given by,

a) At y = 0, T = `T_{s}`
b) At y = `δ_{th}`, (`T_{s}` – `T`) = 0.99(`T_{s}` – `T_{\infty}`)
c) At y > `δ_{th}`, `T` = `T_{\infty}`
d) At x = 0, `δ_{th}` = 0

Thermal boundary layer thickness for flat plate:

It is the perpendicular distance from the surface of the plate to the point in a fluid where the temperature gradient with respect to the height (dt/dy) becomes zero.

It is given by,

`\delta _{th}=\frac{\delta }{(Pr)^{\frac{1}{3}}}`

Where,

δ = Hydrodynamic boundary layer thickness
Pr = Prandtl number