Conduction heat transfer: Definition, Equation, Types, Examples [with Pdf]

Conduction is one of the three modes of heat transfer while the other two are convection and radiation. There are several practical instances of conduction heat transfer in everyday life, in which heat is transferred without producing motion in the molecules of a substance.

What is Conduction heat transfer?

Conduction is the mode of heat transfer in which the transfer of heat from one position to another position is done by means of molecular vibration without changing its lattice position. The heat transfer by conduction is mostly considered in the case of solid materials in which the molecules has the same lattice position throughout the heat transfer process.

It also occurs in liquid or gas molecules, When the motion of the molecules is not considered.

The heat transfer by the conduction takes place by the molecular vibration and by the movement of electrons.

Some of the real world examples of conduction are as follows:

• During the ironing of clothes, the heat is transferred from iron to cloth by conduction
• The handle of the pan kept on the gas stove becomes hot even if it is not directly subjected to the heat. This occurs because the heat is transferred from the pan to the handle by conduction.
• The components attached to the vehicle engines become hot as it gains heat by conduction from the engine.

Fourier’s law used for conduction heat transfer:

The Fourier law of heat conduction states that the rate of heat transfer in a homogeneous solid material is directly proportional to the temperature gradient in the direction of heat flow (`\frac{dT}{dx}`) and area of a cross-section perpendicular to the direction of flow.

Mathematticaly, the fourier law can be expressed as,

Q ∝ A `\frac{dt}{dx}`

Q = – KA .`\frac{dt}{dx}`

Where,
`\frac{dt}{dx}` = Temperature gradient in the direction of heat flow
A = Cross-sectional area
K = Thermal conductivity

Thermal conductivity and Thermal resistance:

Thermal conductivity:

Thermal conductivity is the ability of a material to transfer heat through it. Hence the material with higher thermal conductivity has a higher rate of heat transfer and the material with less thermal conductivity shows a lower rate of heat transfer. Thermal conductivity is denoted by the symbol ‘K’.

From the Fourier law of conduction, the magnitude of thermal conductivity can be given by,

`K=\frac{Q}{A.\frac{dt}{dx}}`

Therefore, the thermal conductivity can be defined as the rate of heat transfer per unit cross-sectional area and per unit temperature gradient in the direction of heat flow.

The unit of thermal conductivity in the SI system is given by,

`K=\frac{Q}{A.\frac{dt}{dx}}` = `\frac{W}{m^{2}.\frac{K}{m}}` =W/mK

Therefore the SI unit of thermal conductivity is W/m.K

Similarly the unit of thermal conductivity in FPS system is given by,

`K=\frac{Q}{A.\frac{dt}{dx}}` = `\frac{\text{Btu/hr}}{ft^{2}.\frac{ ° F}{ft}}`

K = Btu/hr.ft.°F

Therefore the FPS unit of thermal conductivity is Btu/hr.Ft.°F.

Factors affecting thermal conductivity of materials:

The thermal conductivity of a material is influenced by the following factors:-

1) Presence of free electrons:

The free electrons easily travel into the material hence it can transfer the heat at a faster rate.
Hence as the number of free electrons present in the material increases, the thermal conductivity of the material also increases.

The number of free electrons present in metals is higher therefore metals have higher thermal conductivity.

2) Presence of impurity:

The thermal conductivity of the material is higher in its pure form. The thermal conductivity of material decreases with an increase in impurities or alloying elements.
Example: The thermal conductivity of pure copper is higher than brass.

3) Density:

The thermal conductivity of material increases with an increase in its density because of the increase in the rate of molecular collision.

4) Temperature:

In the case of solid materials as the temperature increases, the vibration of molecules also increases, and therefore the movement of free electrons decreases, and hence the thermal conductivity decreases.

In the case of liquids as the temperature increases the density of liquid decreases. Therefore the thermal conductivity of liquid decreases.

5) Material structure:

The crystalline structure has a higher rate of thermal conductivity while the amorphous material has a lesser value of thermal conductivity.

6) Presence of moisture:

The thermal conductivity of material increases with an increase in moisture content in the material.

Thermal resistance:

Thermal resistance is the resistance to the conduction heat transfer that is given by the ratio of the thickness of the object to the product of thermal conductivity and area of cross-section.

Thermal resistance is also known as the reciprocal of thermal conductance.

Mathematically it is expressed as,

`R_{th}=\frac{x}{KA}`

Therefore the Fourier equation for heat conduction can be written as,

`Q=-\frac{\Deltat}{R_{th}}`

The SI unit of thermal resistance is given by,

`R_{th}=\frac{x}{KA}` = `\frac{m}{[\frac{W}{m.K}][m^{2}]}`

`R_{th}=\frac{K}{W}`

Therefore SI unit of thermal resistance is K/W

The FPS unit of thermal resistance is given by,

`R_{th}=\frac{x}{KA}` = `\frac{ft}{[\text{Btu/hr}.ft. °F][ft^{2}]}`

`R_{th}` = °F.hr/Btu

Therefore the FPS unit of thermal resistance is °F.hr/Btu.

Thermal resistance for the composite section:

The composite section consists of a number of layers of different materials. These layers are arranged in series in the direction of heat flow or in parallel to the direction of heat flow.

Here are the methods to find the equivalent resistance for both types of arrangements.

1) Layers in series:

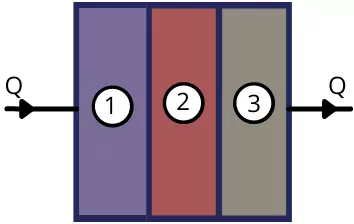
For n number of layers of heat transfering bodies arranged in series, the equivalent thermal resistance is given by,

`R_{th(eq)}=R_{th(1)}+R_{th(2)}`+`R_{th(3)}+\cdots R_{th(n)}`

2) Layers in parallel:

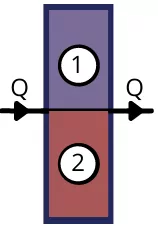
For n number of heat transferring bodies arranged parallelly to the direction of heat flow, the equivalent thermal resistance is given by,

`\frac{1}{R_{th(eq)}}=\frac{1}{R_{th(1)}}`+`\frac{1}{R_{th(2)}}+\cdots \frac{1}{R_{th(n)}}`

Conduction heat transfer equation:

The heat conduction equation shows the heat distribution in the object over time. The equations for heat conduction for the different coordinate systems are given below:-

A) Heat conduction equation in cartesian coordinates:

The general heat conduction equation in cartesian coordinates is given below:

`\frac{\partial }{\partial x}(K_{x}\frac{\partial t}{\partial x})+\frac{\partial }{\partial y}(K_{y}\frac{\partial t}{\partial y})`+`\frac{\partial }{\partial z}(K_{z}\frac{\partial t}{\partial z})+q_{g}=\rho C\frac{\partial t}{\partial \tau }`

Where,
∂t/∂x = Temperature gradient along x-direction
∂t/∂y = Temperature gradient along y direction
∂t/∂z = Temperature gradient along z direction
Kx, Ky, Kz = Thermal conductivity in X, Y, and Z direction
`q_{g}` = Rate of heat generation per unit volume
∂t/∂τ = Rate of temperature change with respect to time
ρ = Density of the material
C = Specific heat

For constant thermal conductivity:-

For constant thermal conductivity in X, Y, and Z-direction, the equation is reduced as,

`\frac{\partial ^{2}t}{\partial x^{2}}+\frac{\partial ^{2}t}{\partial y^{2}}`+`\frac{\partial ^{2}t}{\partial z^{2}}+\frac{q_{g}}{K}=\frac{1}{\alpha }\frac{\partial t}{\partial \tau }`

Where, α = `\frac{K}{\rho\times C}` = Thermal diffusivity

For steady-state heat conduction with constant thermal conductivity:-

For steady-state heat conduction (`\frac{\partial t}{\partial \tau }` = 0) with constant thermal conductivity, the equation can be reduced as,

`\frac{\partial ^{2}t}{\partial x^{2}}+\frac{\partial ^{2}t}{\partial y^{2}}`+`\frac{\partial ^{2}t}{\partial z^{2}}+\frac{q_{g}}{K}=0`

For no heat generation, steady-state conduction and for constant thermal conductivity:

For no heat generation (`q_{g}=0`), steady-state conduction and for constant thermal conductivity, the equation can be reduced as,

`\frac{\partial ^{2}t}{\partial x^{2}}+\frac{\partial ^{2}t}{\partial y^{2}}`+`\frac{\partial ^{2}t}{\partial z^{2}}=0`

B) Heat conduction equation in cylindrical coordinates:

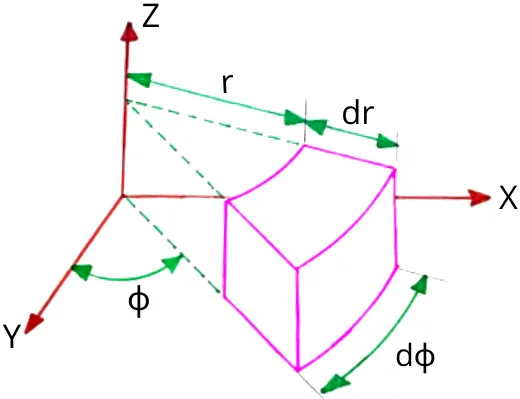
The equation is applicable for the objects having cylindrical shape.

The general heat conduction equation in cylindrical coordinates is given by,

`{[\frac{\partial ^{2}t}{\partial r^{2}}]+\frac{1}{r}\frac{\partial t}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}t}{\partial \phi ^{2}}`+`\frac{\partial ^{2}t}{\partial z^{2}}}+q_{g}=\frac{1}{\alpha }\frac{\partial t}{\partial \tau `

C) Heat conduction equation in spherical coordinates:

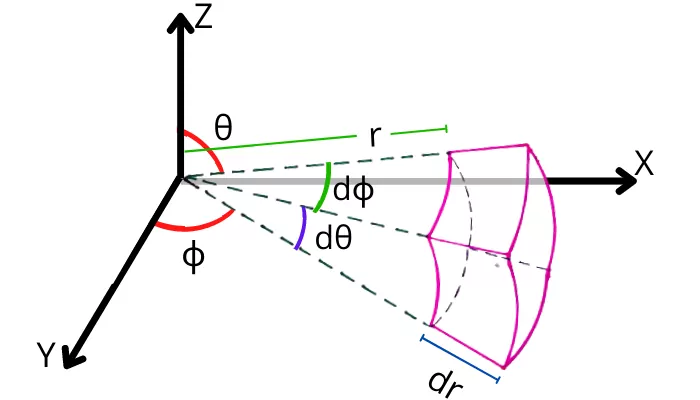
The equation is applicable for the object having spherical shape.
General heat conduction equation in spherical coordinates is given by,

`[\frac{1}{r^{2}sin^{2}\theta }.\frac{\partial ^{2}t}{\partial \phi ^{2}}`+`\frac{1}{r^{2}sin\theta }.\frac{\partial }{\partial \theta }(sin\theta \frac{\partial t}{\partial \theta })`+`\frac{1}{r^{2}}\frac{\partial }{\partial r }(r^{2} \frac{\partial t}{\partial r })]`+ ` \frac{q_{g}}{K}=\frac{1}{\alpha }\frac{\partial t}{\partial \tau }`

Types of conduction heat transfer:

The conduction heat transfer is classified on the basis of temperature variation with respect to time and temperature variation with respect to distance.

Based on temperature variation with respect to time, the conduction heat transfer is classified as,

1) Steady state heat conduction:

In steady state heat conduction, the temperature of an object doesn’t change with respect to time or we can say that in steady-state conduction the change in temperature with respect to time is negligible.

Mathematically it is stated as,

`\frac{\partial t}{\partial \tau }=0`

Where,
∂t = Change in temperature
∂`\tau ` = Time interval

Example: Heat generated due to the electric current.

2) Unsteady state heat conduction:

In unsteady state heat conduction, the temperature of an object changes with respect to time.
Hence in this case, the temperature change with respect to time is considerable.

Mathematically it is expressed as,

`\frac{\partial t}{\partial \tau }\ne 0`

Example: Heating or Cooling of water

Based on temperature variation with respect to space, the conduction heat transfer is classified as,

1] One-dimensional heat conduction:

In one-dimensional heat conduction, the temperature gradient in the two dimensions is negligible in comparison with the third dimension.

Mathematically, it is expressed as,

`\frac{\partial ^{2}t}{\partial x^{2}}`>>`\frac{\partial ^{2}t}{\partial y^{2}}` and `\frac{\partial ^{2}t}{\partial z^{2}}`

`\therefore \frac{\partial ^{2}t}{\partial y^{2}}` and `\frac{\partial ^{2}t}{\partial z^{2}}\approx 0`

2] Two dimensional heat conduction:

In two-dimensional heat conduction, the temperature gradient in one dimension is negligible in comparison with the other two dimensions.

Mathematically, it is expressed as,

`\frac{\partial ^{2}t}{\partial x^{2}} and \frac{\partial ^{2}t}{\partial y^{2}}`>>`\frac{\partial ^{2}t}{\partial z^{2}}`

`\therefore \frac{\partial ^{2}t}{\partial z^{2}}\approx 0`

3] Three dimensional heat conduction:

In three-dimensional heat conduction, the temperature gradient is present in all three dimensions.

`\frac{\partial ^{2}t}{\partial x^{2}} and \frac{\partial ^{2}t}{\partial y^{2}}` and `\frac{\partial ^{2}t}{\partial z^{2}}` `\neq` 0

One dimensional steady state heat conduction:

Following are the different cases of one-dimensional steady-state heat transfer:-

A) Heat conduction through a plane wall:-

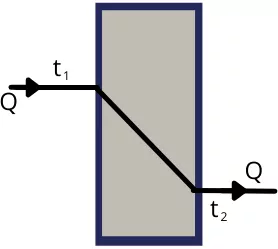
The one-dimensional steady-state heat conduction through the plane wall is given by,

`Q=\frac{(t_{1}-t_{2})}{\frac{L}{KA}}`

It is also written as,

`Q=\frac{(t_{1}-t_{2})}{R_{th}}` —-[as `R_{th}=\frac{L}{KA}`]

Where
`t_{1}-t_{2}` = Temperature difference between two surfaces
L = Thickness of the wall
K = Thermal conductivity of the plane wall
A = Area of a cross-section of plane wall

B) Heat conduction through composite wall:

The composite plane walls are made by arranging layers of the different materials in series or in parallel.

1) Walls in series:

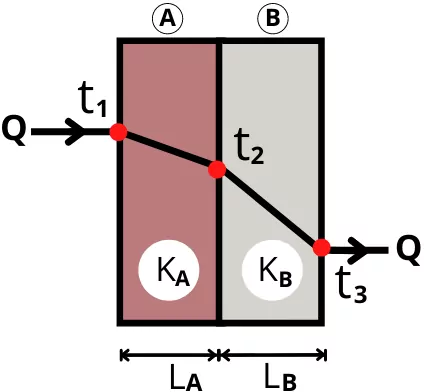
For plane was arranged in series, the rate of heat transfer is given by,

Q = `Q_{1-3} = Q_{1-2} = Q_{2-3}`

Q=`\frac{t_{1}-t_{3}}{R_{th(A)}+R_{th(B)}}` = `\frac{t_{1}-t_{2}}{R_{th(A)}}` = `\frac{t_{2}-t_{3}}{R_{th(B)}}`

Q=`\frac{t_{1}-t_{3}}{\frac{L_{A}}{K_{A}A_{A}}+\frac{L_{B}}{K_{B}A_{B}}}` = `\frac{t_{1}-t_{2}}{\frac{L_{A}}{K_{A}A_{A}}}` = `\frac{t_{2}-t_{3}}{\frac{L_{B}}{K_{B}A_{B}}}`

2) Walls in parallel:

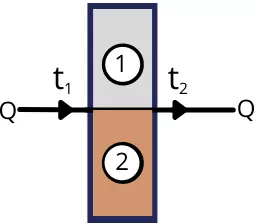
For plain wall arranged parallel, the rate of heat transfer is given by,

Q = `Q_{1} + Q_{2}`

Q =`\frac{t_{1}-t_{2}}{\frac{L_{1}}{K_{1}A_{1}}}` + `\frac{t_{1}-t_{2}}{\frac{L_{2}}{K_{2}A_{2}}}`

C) Heat conduction through hollow cylinder:

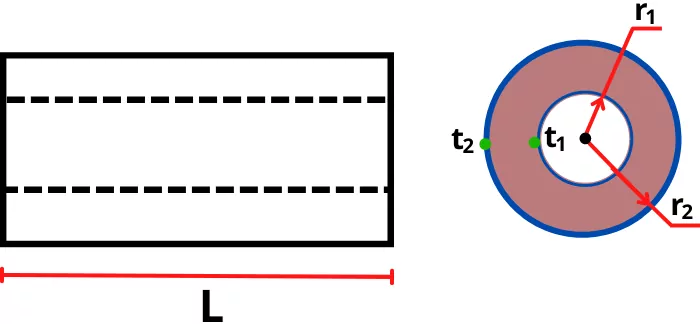
The heat transfer by conduction through hollow cylindrical shape is given by,

Q = `\frac{t_{1}-t_{2}}{\frac{ln(\frac{r_{2}}{r_{1}})}{2\pi KL}}`

Where,
`t_{1}` = Inner surface temperature
`t_{2}` = Outer surface temperature
`r_{1}` = Inner radius of cylinder
`r_{2}` = Outer radius of cylinder
K = Thermal conductivity of cylinder
L = Length of cylinder

For cyclinder `R_{th}` =`\frac{ln(\frac{r_{2}}{r_{1}})}{2\pi KL}` , therefore the equation can also written as,

Q =`\frac{t_{1}-t_{2}}{R_{th}}`

D) Heat conduction through hollow sphere:

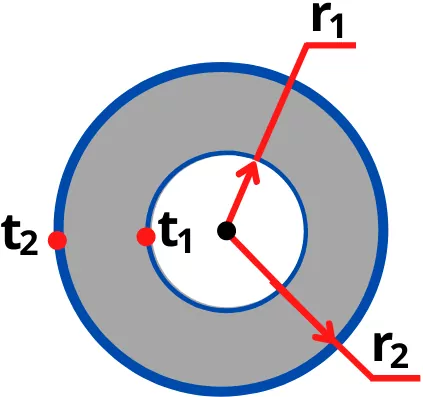
The heat transfer by conduction through hollow sphere is given by,

Q = `\frac{t_{1}-t_{2}}{\frac{(r_{2}-r_{1})}{4\pi K r_{1}r_{2}}}`

Where,
`r_{1}` = Inner radius of sphere
`r_{2}` = Outer radius of sphere
K = Thermal conductivity
`t_{1}` = Inner surface temperature
`t_{2}` = Outer surface temperature

For sphere, the thermal resistance is given by

`R_{th}` =`\frac{(r_{2}-r_{1})}{4\pi K r_{1}r_{2}}`

Therefore the equation can also written as,

Q = `\frac{t_{1}-t_{2}}{R_{th}}`

Conduction heat transfer examples:

1] For the wall shown below, the area perpendicular to the direction of flow is 1.5 m². The temperature at the left side of the wall is 1500°C and at the right side is 40°C. Thus find the rate of heat transfer through the wall. (`K_{A}` = 0.65 W/mK, `K_{B}` = 0.3 W/mK)

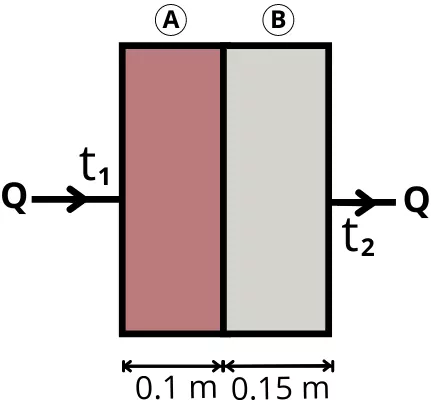
Given:

`K_{A}` = 0.65 W/mK
`K_{B}` = 0.3 W/mK
A = 1.5 m²
`t_{1}` = 1500 °C = 1773 K
`t_{2}` = 40 °C = 313 K
`L_{A}` = 0.1 m
`L_{B}` = 0.15 m

Solution:

Total thermal resistance for the wall is given as follows,

`R_{th}` = `R_{th(1)}+R_{th(2)}`

`R_{th}` = `\frac{L_{A}}{K_{A}.A}` + `\frac{L_{B}}{K_{B}.A}`

`R_{th}` = `\frac{0.1}{0.65 \times 1.5}` + `\frac{0.15}{0.3 \times 1.5}`

`\mathbf{R_{th}}` = 0.435 K/W

The rate of heat transfer through the wall is given by,

`Q=\frac{(t_{1}-t_{2})}{R_{th}}`

`Q=\frac{1773 – 313}{0.435}`

Q = 3356.32 W

This is the rate of heat transfer through the wall.

---

2] The hollow cylinder has an inside radius of 0.5 m, an outside radius of 1 m, and a length of 1.5 m. The temperature on the inside surface of the cylindrical wall is 1650°C and on the outside surface is 25°C. Thus find the rate of heat transfer through the cylinder. (`K_{\text{cylinder}}` = 0.55 W/mK)

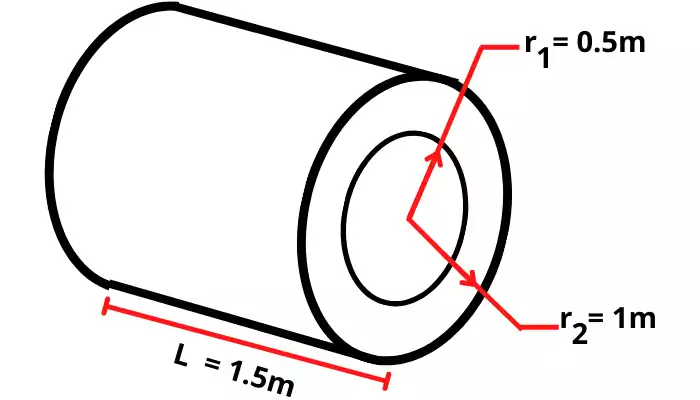
Given:

`K_{\text{cylinder}}` = 0.55 W/mK
`r_{1}` = 0.5 m
`r_{2}` = 1 m
`t_{1}` = 1650°C = 1923 K
`t_{2}` = 25 °C = 298 K
L = 1.5 m

Solution:

The thermal resistance for the cylindrical surface is given by,

`R_{th}` =`\frac{ln(\frac{r_{2}}{r_{1}})}{2\pi KL}`

`R_{th}` =`\frac{ln(\frac{1}{0.5})}{2\pi \times 0.55 \times 1.5}`

`R_{th}` = 0.1337 m

`R_{th}` = 0.1337 m

The heat transferred outside of the cylinder is given by,

Q =`\frac{t_{1}-t_{2}}{R_{th}}`

Q =`\frac{1923 – 298}{0.1337}`

Q = 12154.07 W

FAQs: