What is Thermal time constant?
The thermal time constant is the time taken by the system to undergo temperature change equal to 63.2% of the initial temperature difference between the system and its surrounding. It can be considered for the system undergoing cooling or heating.
In other words, it is time taken by the system to attain following condition,
Temperature change in system = 63.2% (Initial difference between Tsystem & Tsurrounding)
Let’s discuss this with an example.
In the below figure, the solid body is subjected to cooling.
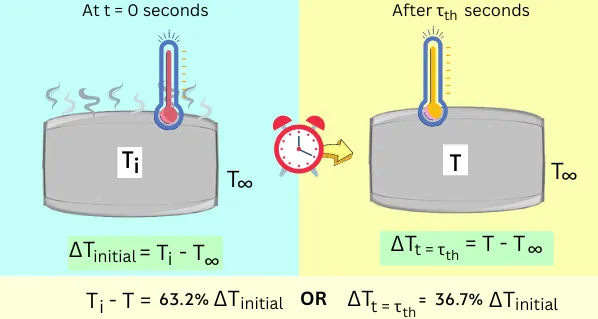
Consider, initially the body is at temperature Ti and the surrounding is at T∞ temperature. After the time interval τth seconds, consider the temperature of the body as T.
Thus `\tau_{th}` is the time interval, when,
`\mathbf{T_(\text{i}} – T = 63.2% \text{of} (T_{\text{i}} – T_{\infty})}`
OR
`\mathbf{T_(i} – T = 0.632\times(T_{\text{i}} – T_{\infty})}`
It means that, at τth, the system covers around 63.2% of the initial temperature difference.
The thermal time constant is important to understand the response of a system to the surrounding temperature changes.
The thermal time constant is denoted by the symbol ‘τth‘ and has an SI unit as seconds (s).
In this article, we’re going to discuss:
- Temperature relation at τth for cooling and heating:
- Relation between `\DeltaT_{t=\tau_{th}}` and `\DeltaT_{\text{initial}}`:
- Thermal time constant equation:
- Significance of thermal time constant:
- Relation between temperature difference at `t=\tau_{th}`:
- Solved Numerical:
- FAQ’s:
Temperature relation at τth for cooling and heating:
In the case of cooling, the below temperature Vs time graph shows the temperature relation at a time interval of τth.
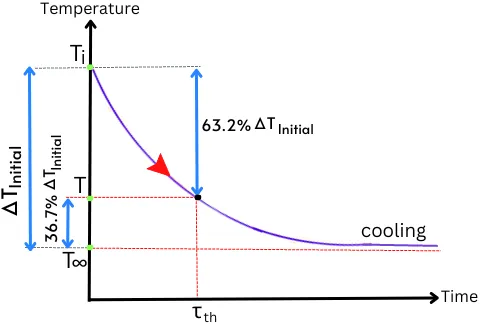
For cooling, the temperature relation after a time interval of τth is given by,
`T_{i} – T = 63.2%(T_{i} – T_{\infty})`
In the case of heating, the below temperature Vs time graph shows the temperature relation at a time interval of τth.
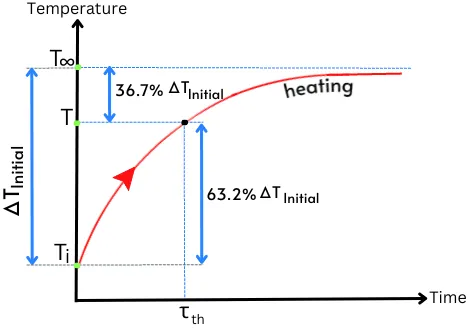
For heating, the temperature relation after a time interval of τth is given by,
`T – T_{i} = 63.2%(T_{\infty} – T_{i})`
Relation between `\DeltaT_{t=\tau_{th}}` and `\DeltaT_{\text{initial}}`:
At τth, the relation between the final temperature difference `\DeltaT_{t=\tau_{th}}` (between the system and its surrounding) and the initial temperature difference `\DeltaT_{\text{initial}}` is given by,
`\DeltaT_{t=\tau_{th}} = (1 – 0.632)\DeltaT_{\text{initial}}`
`\DeltaT_{t=\tau_{th}} = 36.7%\DeltaT_{\text{initial}}`
Thermal time constant equation:
The thermal time constant is given by the following equation,
`\tau_{th}=\frac{\rho VC}{hA_{S}}`
Where,
ρ = Density of the body
V = Volume of the body
C = Specific heat of an object
h = Convective heat transfer coefficient
As = Surface area of the body
The above factors decide the thermal time constant of the object or system.
By using a thermal time constant, the lumped system equation is also rewritten as,
`\frac{T-T_{\infty}}{T_{i}-T_{\infty}}=e^{-\frac{t}{\tau}}`
Significance of thermal time constant:
It has following significances:
- It indicates the response of the system or object to the change in the surrounding temperature.
- The system with a lower time constant takes less time to achieve temperature change.
- The system with a higher value of the time constant takes much time to achieve temperature change.
Relation between temperature difference at `t=\tau_{th}`:
To check the relation between temperature difference at `t=\tau_{th}`, put the time interval equal to `\tau_{th}` in the equation of lumped system analysis.
`\frac{T-T_{\infty}}{T_{i}-T_{\infty}}=e^{-\frac{hA_{s}}{\rho VC}t}`
`\frac{T-T_{\infty}}{T_{i}-T_{\infty}}=e^{-\frac{t}{\tau}}`
`\frac{T-T_{\infty}}{T_{i}-T_{\infty}}=e^{-1}`
`\therefore (T-T_{\infty})=0.367(T_{i}-T_{\infty})`
`\therefore \Delta T_{t = \tau_{th}}=0.367\Delta T_{\text{intial}}`
`\therefore \Delta T_{t = \tau_{th}}=36.7\%\Delta T_{\text{intial}}`
From the above equation, it is clear that after the interval of `t=\tau_{th}` the temperature difference between the system and surroundings is equal to 36.7% of the initial temperature difference.
Therefore at `t=\tau_{th}`, the system covers a temperature difference equal to 63.2% of the initial temperature difference.
Solved Numerical:
1] Find the thermal time constant for a spherical object with a radius of 2.5 mm. (Assume h = 350 W/m2°C, K = 25 W/m°C. density = 7600 Kg/m3, specific heat = 300 J/Kg°C)
Given:
R = 2.5 mm = `2.5 \times 10^{-3}` m
h = 350 W/m2°C
K = 25 W/m°C
`\rho` = 7600 Kg/m3
C = 300 J/Kg°C
Solution:
The surface area of the spherical object,
`A_{S} = 4\piR^{2} = 4\pi\times(2.5 \times 10^{-3})^{2}`
`A_{S} = 7.853\times10^{-5}`m2
Volume of the spherical object,
`V = \frac{4}{3}.\pi.R^{3}`
V = `\frac{4}{3}.\pi.(2.5 \times 10^{-3})^{3}`
V = `6.544\times10^{-8}` m3
The thermal time constant is given by,
`\tau_{th}=\frac{\rho VC}{hA_{S}}`
`\tau_{th}=\frac{7600\times(6.544\times10^{-8})\times300}{350\times(7.853\times10^{-5})}`
`\tau_{th}` = 5.428 seconds
2] An object subjected to cooling is initially at 300°C and its surroundings are at 50°C. Find the temperature of the object at the time equal to 3τth.
Given:
Ti = 300°C
T∞ = 50°C
t = 3τth
Solution:
The temperature of the object after a time interval of 3τth is given by,
`\frac{T-T_{\infty}}{T_{i}-T_{\infty}}=e^{-\frac{t}{\tau}}`
`\frac{T-50}{300-50}=e^{-\frac{3\tau}{\tau}}`
`\frac{T-50}{300-50}=e^{-3}`
T = 62.44 °C
Thus, after the interval of 3τth, the temperature of the object reaches 62.44 °C.
FAQ’s:
-
Which factors affect the thermal time constant?
The thermal time constant depends on the following factors:
Density of system, Volume, Surface area, Convective heat transfer coefficient, Specific heat of the material.
