Contents:
What is lumped system analysis and when is it applicable?
The lumped system analysis is the method used for the analysis of transient heat transfer systems.
The method is used when there is no temperature gradient present in the object to be analyzed for the complete heat transfer process.
It means that the temperature of the body should be uniform throughout the object. As in this case, the thermal conductivity of the object is considered infinite, therefore the thermal resistance inside of the body is minimum.
Lumped system analysis is used in the smallest bodies whose thermal conductivity is high.
Therefore the lumped system analysis is applicable for the system only when the biot number is less than 0.1.
Bi < 0.1
Where, the biot number is given by,
`Bi=\frac{Lc \times h}{K}`
Where,
Lc is the characteristic length
Bi = Biot number
K = Thermal conductivity
h = Convective heat transfer coefficient
lumped system analysis assumptions:
The assumptions for lumped system analysis are as follows:-
1) The temperature of the body is uniform at any point.
2) The temperature is the function of time.
3) Internal conductive resistance is minimum.
4) The object has infinite thermal conductivity.
Lumped system analysis derivation:
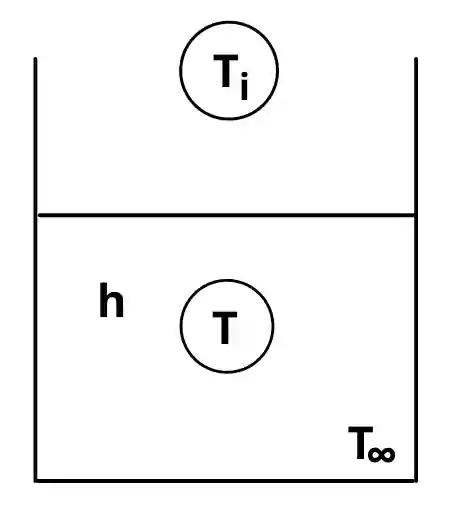
Consider the object with surface area A, volume V, and thermal conductivity K and at the initial temperature, Ti enters into the fluid at temperature `T_{ \infty}`.
For the object shown above, the heat transfer by convection is equal to the change in internal energy of that object.
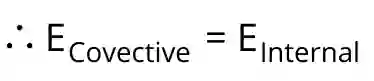
`\therefore hA(T-T_{ \infty })=-\frac{d}{dt}(\rho VCT)`
`-\frac{hA}{\rho VC} (T-T_{ \infty })=\frac{dT}{dt}`
`-\frac{hA}{\rho VC}. dt=\frac{1}{T-T_{ \infty }}.dT`
Integrating both sides,
`\int -\frac{hA}{\rho VC}. dt=\int \frac{1}{T-T_{ \infty }}.dT`
`-\frac{hAT}{\rho VC}=ln(T-T_{ \infty })+C`—–Equation [1]
Now to find value of constant C, put t = 0 at T = Ti
`-\frac{hA(0)}{\rho VC}=ln(T_{i}-T_{ \infty })+C`
`\therefore C=-ln(T_{i}-T_{ \infty})`
Putting value of C in equation [1]
`-\frac{hAt}{\rho VC}=ln(T-T_{ \infty })-ln(T_{i}-T_{ \infty })`
`-\frac{hAt}{\rho VC}=ln\frac{T-T_{ \infty }}{T_{i}-T_{ \infty }}`
`e^{-\frac{hAt}{\rho VC}}=\frac{T-T_{ \infty }}{T_{i}-T_{ \infty }}`
`\frac{T-T_{ \infty }}{T_{i}-T_{ \infty }}=e^{-\frac{hAt}{\rho VC}}`
This is the equation of lumped system analysis.
The equation for lumped system analysis in the form of Fourier and biot number is written as,
`\frac{T-T_{ \infty }}{T_{i}-T_{ \infty }}=e^{-F_{O}Bi}`
Where,
- Fo = Fourier number
- Bi = Biot number
Lumped system analysis neumerical:
Here are the numerical on lumped system analysis that will help you to understand the method easily.
A sphere of radius 10 mm at a temperature of 600 K is dipped into the liquid at 300 Kelvin with a convective coefficient of 100 w/m.k. find the time required to become temperature of the sphere equals to 500 K
The sphere has, c = 375 J/Kg.K
ρ = 8700 Kg/m3
K = 360 w/m.K
Given:
r = 10mm = 0.01 m
Ti = 600 K
T∞ = 300 K
T = 500 K
h = 100 W/m.K
c = 375 J/Kg.K
ρ = 8700 Kg/m3
K = 360 w/m.K
1] Check for applicability of lumped system:
The volume of Sphere is (V),
V= (4/3)× π x r^3 = (4/3)×π.(0.01)^3 = 4.188 × 10^(-6) m^3
The surface area of Sphere is (A),
A= 4πr^2= 4π×(0.01)^2 = 1.256 × 10^(-3) m^2
The characteristics length of sphere is given by (Lc),
Lc = V/A = (4.188 × 10^(-6)) / (1.256 × 10^(-3))
Lc = 3.33×10^(-3)
The biot number is given by (Bi),
Bi = (Lc.h) / K
Bi = (3.33×10^(-3)× 100) / 360
Bi = 9.85 × 10^(-4)
As Bi < 0.1
Hence the lumped system analysis is applicable.
2] Find time required to attain temperature (t):
`\frac{T-T_{ \infty }}{T_{i}-T_{ \infty }}=e^{-\frac{hAt}{\rho VC}}`
`\frac{500-300}{600-300}=e^{-\frac{100(1.256\times 10^{-3})\times t}{8700\times (4.188\times 10^{-3})\times 375}}`
t = 44.10 seconds
Hence, the Time required to become the temperature of the sphere equals 500 k is t = 44.10 seconds
Read also:
