What is biot number?
Biot number is the ratio of internal conductive resistance within the body to the external convective resistance at the surface of the body.
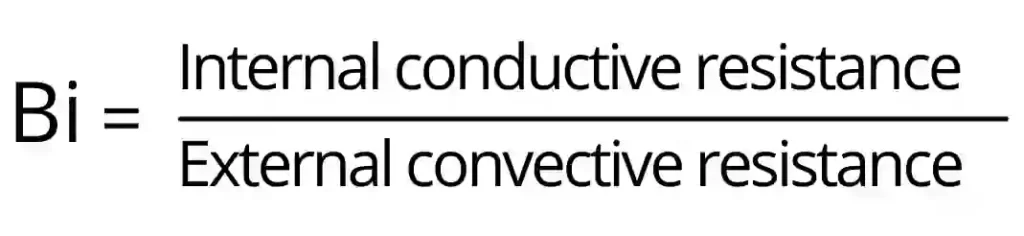
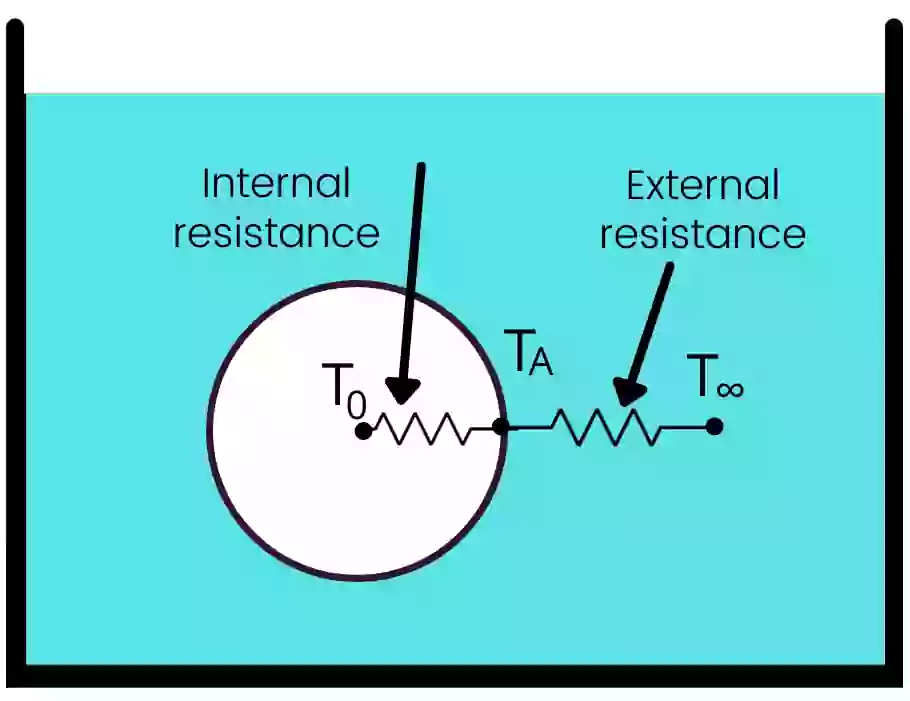
This number gives the relation between internal resistance and external resistance for heat transfer. This equation is recognized by the name of French physicist Jean Baptiste Biot.
In this article, we’re going to discuss:
- Significance of biot number in heat transfer:
- Biot number equation:
- Biot number formula for simple shapes:
- Biot number lumped capacitance:
Significance of biot number in heat transfer:
The biot number has the following significances:-
1) The biot number shows the relation between the internal conductive resistance and convective resistance at the surface of the object.
2) It is used as a criterion for lumped system analysis.
3) The higher value of the biot number indicates that the internal resistance in the object is higher than external resistance.
4) The lower value of the biot number indicates that the conductive resistance of an object is comparatively lower than external resistance.
5) Biot number along with Fourier number helps to analyze objects by lumped system analysis.
Biot number equation:
The biot number is given by,

Internal conductive resistance is given by, `\frac{L_{C}}{KA}`
And the external convective resistance is given by, `\frac{1}{hA}`
`\therefore Bi=\frac{\frac{L_{C}}{KA}}{\frac{1}{hA}}`
`Bi=\frac{hL_{C}}{K}`
Where,
h= Convective heat transfer coefficient
K= Thermal conductivity
Lc= Characteristic length = volume/area= V/A
Note:-
A] If the Bi<40 : Therefore,
i) External convective resistance is much smaller.
ii) Difference between surface temperature and surrounding temperature is negligible.
B] If Bi>40 : Therefore,
i) Internal conductive resistance is minimum as the body has infinite thermal conductivity.
ii) Difference between core temperature and surface temperature is negligible.
Biot number formula for simple shapes:
A] Biot number for sphere:
The characteristic length for a is given by,
`L_{C}=\frac{V}{A}`
For sphere, V = (4/3).π.r³ and A=4πr²
Therefore,
`L_{C}=\frac{\frac{4}{3}\pi r^{3}}{4\pi r^{2}}`
`L_{C}=\frac{r}{3}`
Hence the biot number for sphere is given by,
`Bi=\frac{hL_{c}}{K}`
`Bi=\frac{(\frac{r}{3})h}{K}`
`Bi=\frac{rh}{3K}`
2) Biot number for cylinder:
The characteristics length of the cylinder is given by,
`L_{C}=\frac{V}{A}`
For cylinder, V= π.r ² .h and A= 2πrh
Therefore,
`L_{C}=\frac{\pi r^{2}h}{2\pi rh}`
`L_{C}=\frac{r}{2}`
Hence the biot number for sphere is given by,
`Bi=\frac{hL_{c}}{K}`
`Bi=\frac{(\frac{r}{2})h}{K}`
`Bi=\frac{rh}{2K}`
Biot number lumped capacitance:
Biot number lumped capacitance is the method for transient heat transfer analysis in which the temperature of the body varies with time only.
A) Assumptions of lumped capacitance method:
i] The temperature is the function of time.
ii] The temperature throughout the body is uniform. It means that,
(dT/dx), (dT/dy), (dT/dz) = 0
iii] Thermal conductivity of the body is infinite.
To solve the problem by lumped capacitance the biot number should be less than 0.1
Bi < 0.1
B) Formula for lumped capacitance method:
`\frac{T-T_{\infty}}{T_{i}-T_{\infty}}=exp[-\frac{hAt}{V\rho C}]`
Where,
T= Final temperature after an interval of t.
T ∞ = Surrounding temperature
T i = Initial temperature of body
h = Convective heat transfer coefficient
A = Surface area of object
t = Time of heating/ cooling
V = Volume of object
ρ = Density of object
C = Heat capacity of object
The equation of lumped capacity method can be also written as,
`\frac{T-T_{\infty}}{T_{i}-T_{\infty}}=exp[-Bi.Fo]`
Read also: